Знайти особливі границі важко не тільки багатьом студентам першого, другого курсу навчання, що вивчають теорію границь, а й частині викладачів, що навчають студентів.
Формула першої особливої границі
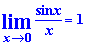 Наслідки першої особливості границі запишемо формулами
Наслідки першої особливості границі запишемо формулами
1. 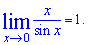 2.
2. 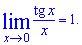 3.
3. 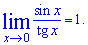 4.
4. 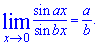 Але самі по собі загальні формули чудових границь нікому на екзамені чи тесті не допомагають. Суть в тому, що реальні завдання побудовані так, що до записаних вище формул потрібно, ще прийти. І більшість студентів, які пропускають пари, заочно вивчають цей курс або мають викладачів, які самі не завжди розуміють про що пояснюють не можуть виконати самих елементарних прикладів на чудові границі. З формул першої особливої границі бачимо, що з її допомогою можна досліджувати невизначеності типу нуль поділити на нуль
Але самі по собі загальні формули чудових границь нікому на екзамені чи тесті не допомагають. Суть в тому, що реальні завдання побудовані так, що до записаних вище формул потрібно, ще прийти. І більшість студентів, які пропускають пари, заочно вивчають цей курс або мають викладачів, які самі не завжди розуміють про що пояснюють не можуть виконати самих елементарних прикладів на чудові границі. З формул першої особливої границі бачимо, що з її допомогою можна досліджувати невизначеності типу нуль поділити на нуль для виразів з тригонометричними функціями. Розглянемо спершу ряд прикладів на першу чудову границю, а тоді розжуємо другу чудову границю.
для виразів з тригонометричними функціями. Розглянемо спершу ряд прикладів на першу чудову границю, а тоді розжуємо другу чудову границю.
Приклад 1. Знайти границю функції sin(7*x)/(5*x)
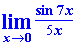 Розв'язок: Як бачите функція під границею близька до першої чудової границі, але сама границя точно не рівна одиниці. В такого роду завданнях на границі слід в знаменнику виділити змінну з таким коефіцієнтом, який міститься при змінній під синусом. В даному випадку слід поділити і помножити на 7
Розв'язок: Як бачите функція під границею близька до першої чудової границі, але сама границя точно не рівна одиниці. В такого роду завданнях на границі слід в знаменнику виділити змінну з таким коефіцієнтом, який міститься при змінній під синусом. В даному випадку слід поділити і помножити на 7
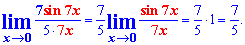
Декому така деталізація здасться зайвою, але більшості студентів, яким важко даються границі допоможе краще зрозуміти правила та засвоїти теоретичний матеріал.
Також, якщо маємо обернений вигляд функції – то це також перша чудова границя. А все тому, що особлива границя рівна одиниці
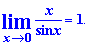
Це саме правило стосується і висновків 1 чудової границі. Тому, якщо Вас спитають "Чому рівна перша чудова границя?" Ви без вагань повинні знати, що це – одиниця.
Приклад 2. Знайти границю функції sin(6x)/tg(11x)
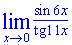 Розв'язок: Для розуміння кінцевого результату розпишемо функцію у вигляді
Розв'язок: Для розуміння кінцевого результату розпишемо функцію у вигляді
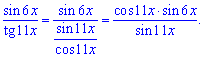
Щоб застосувати правила особливої границі помножимо та поділимо на множники
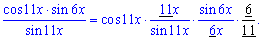
Далі границю добутку функцій розпишемо через добуток границь
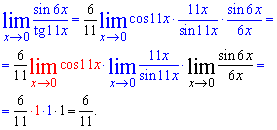
Без складних формул ми знайшли границю часки тригонометричних функцій. Для засвоєння простих формул спробуйте придумати та знайти границю на 2 та 4 формулу наслідку 1 особливої границі. Ми ж розглянемо складніші завдання.
Приклад 3. Обчислити границю (1-cos(x))/x^2
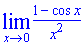 Розв'язок: При перевірці підстановкою отримаємо невизначеність 0/0. Багато кому невідомо, як звести такий приклад до 1 особливої границі. Тут слід використати тригонометричну формулу
Розв'язок: При перевірці підстановкою отримаємо невизначеність 0/0. Багато кому невідомо, як звести такий приклад до 1 особливої границі. Тут слід використати тригонометричну формулу
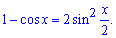
При цьому границя набуде зрозумілого вигляду
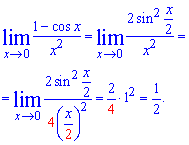
Нам вдалося звести функцію до квадрату особливої границі.
Приклад 4. Знайти границю
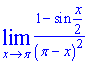 Розв'язок: При підстановці отримаємо знайому особливість 0/0. Проте змінна прямує до Pi, а не нуля. Тому для застосування першої особливої границі виконаємо таку заміну змінної х, щоб нова змінна прямувала до нуля, знаменник позначимо за нову змінну Pi-x=y
Розв'язок: При підстановці отримаємо знайому особливість 0/0. Проте змінна прямує до Pi, а не нуля. Тому для застосування першої особливої границі виконаємо таку заміну змінної х, щоб нова змінна прямувала до нуля, знаменник позначимо за нову змінну Pi-x=y
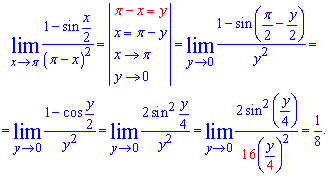
Таким чином використавши тригонометричну формулу, яка наведена в попередньому завданні, приклад зведено до 1 особливої границі.
Приклад 5. Обчислити границю
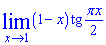 Розв'язок: Спершу неясно, як спростити границю. Але раз є приклад, значить має бути і відповідь. Те що змінна прямує до одиниці дає при підстановці особливість вигляду нуль помножити на безмежність, тому тангенс потрібно замінити за формулою
Розв'язок: Спершу неясно, як спростити границю. Але раз є приклад, значить має бути і відповідь. Те що змінна прямує до одиниці дає при підстановці особливість вигляду нуль помножити на безмежність, тому тангенс потрібно замінити за формулою
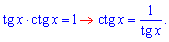
Після цього отримаємо потрібну невизначеність 0/0. Далі виконуємо заміну змінних в границі, та використовуємо періодичність котангенса
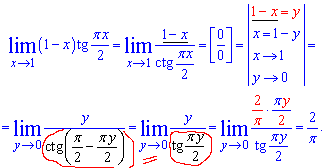
Останні заміни дозволяють використати наслідок 1 особливої границі.
Друга особлива границя рівна експоненті
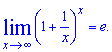 Це класика, до якої в реальних задачах на границі не завжди легко прийти.
Це класика, до якої в реальних задачах на границі не завжди легко прийти.
В обчисленнях Вам також знадобляться границі — наслідки другої особливої границі:
1. 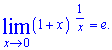 2.
2. 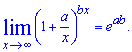 3.
3. 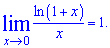 4.
4. 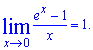
Завдяки другій особливій границі та її наслідкам можна досліджувати невизначеності типу нуль розділити на нуль, одиниця в степені безмежність, та нескінченність розділити на нескінченність, та ще й в такому ж степені
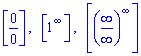
Почнемо для ознайомлення з простих прикладів.
Приклад 6. Обчислити границю
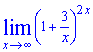 Розв'язок: Напряму застосувати 2 особливу границю не вийде. Спершу слід перетворити показник, щоб він мав вигляд обернений до доданка в дужках
Розв'язок: Напряму застосувати 2 особливу границю не вийде. Спершу слід перетворити показник, щоб він мав вигляд обернений до доданка в дужках
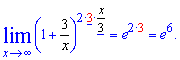
Це і є техніка зведення до 2 чудової границі і по суті – виведення 2 формули наслідку границі.
Приклад 7. Знайти границю
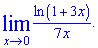 Розв'язок: Маємо завдання на 3 формулу наслідку 2 особливої границі. Підстановка нуля дає особливість типу 0/0. Для зведення границі під правило перетворимо знаменник, щоб при змінній був той самий коефіцієнт, що і в логарифмі
Розв'язок: Маємо завдання на 3 формулу наслідку 2 особливої границі. Підстановка нуля дає особливість типу 0/0. Для зведення границі під правило перетворимо знаменник, щоб при змінній був той самий коефіцієнт, що і в логарифмі
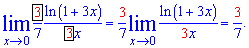
Це також легко зрозуміти та виконати на екзамені. Труднощі у студентів при знаходженні границь починаються із наступних завдань.
Приклад 8. Обчислити границю функції [(x+7)/(x-3)]^(x-2)
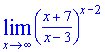 Розв'язок: Маємо особливість типу 1 в степені безмежність. Якщо не вірите, можете всюди замість "ікс" підставити нескінченність та переконатися в цьому. Для зведення під правило поділимо в дужках чисельник на знаменник, для цього попередньо виконаємо маніпуляції
Розв'язок: Маємо особливість типу 1 в степені безмежність. Якщо не вірите, можете всюди замість "ікс" підставити нескінченність та переконатися в цьому. Для зведення під правило поділимо в дужках чисельник на знаменник, для цього попередньо виконаємо маніпуляції
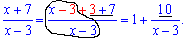
Підставимо вираз у границю та перетворимо під 2 особливу границю
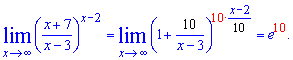
Границя рівна експоненті в 10 степені. Константи, які є доданками при змінній як в дужках так і степені ніякої "погоди" не вносять – про це слід пам'ятати. А якщо Вас запитають викладачі – "Чому не перетворюєте показник?" (для цього прикладу до x-3), то скажіть, що "Коли змінна прямує до безмежності, то до неї хоч додавай 100, хоч віднімай 1000, а границя залишиться такою як і була!".
Є і другий спосіб обчислювати границі такого типу. Про нього розкажемо у наступному завданні.
Приклад 9. Знайти границю 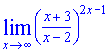 Розв'язок: Цього разу винесемо змінну з чисельника та знаменника та перетворимо одну особливість на іншу. Для отримання кінцевого значення використаємо формулу наслідку 2 особливої границі
Розв'язок: Цього разу винесемо змінну з чисельника та знаменника та перетворимо одну особливість на іншу. Для отримання кінцевого значення використаємо формулу наслідку 2 особливої границі
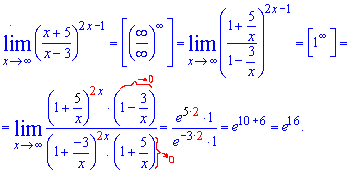
В результаті маніпуляцій отримали експоненту в 16 степені.
Приклад 10. Знайти границю
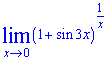 Розв'язок: Задану границю знайти під силу не кожному. Для зведення під 2 особливу границю уявимо, що sin(3x) це змінна, а потрібно перетворити показник
Розв'язок: Задану границю знайти під силу не кожному. Для зведення під 2 особливу границю уявимо, що sin(3x) це змінна, а потрібно перетворити показник
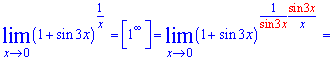
Далі показник перетворюємо як степінь в степені
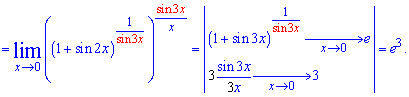
В дужках написані проміжні міркуванні. В результаті використанні першої і другої особливої границі отримали експоненту в кубі.
Приклад 11. Обчислити границю функції sin(2*x)/ln(3*x+1)
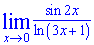 Розв'язок: Маємо невизначеність виду 0/0. Крім цього бачимо, що в дробовій функції чисельник та знаменник слід перетворювати під обидві особливі границі. Виконаємо попередні математичні перетворення
Розв'язок: Маємо невизначеність виду 0/0. Крім цього бачимо, що в дробовій функції чисельник та знаменник слід перетворювати під обидві особливі границі. Виконаємо попередні математичні перетворення
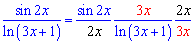
Далі за теорією границя прийме простий вигляд
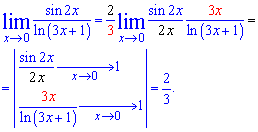
Ось так вільно Ви будете почувати себе на контрольних роботах, тестах, модулях, якщо навчитеся швидко розписувати функції і зводити під першу чи другу особливі границі. Якщо освоїти наведені методики знаходження границь Вам важко, то завжди можете замовити контрольну роботу на границі у нас.
Для цього заповніть форму, вкажіть дані та вкладіть файл із прикладами. Ми допомогли багатьом студентам, зможемо допомогти і Вам!


