Продовжуємо розбирати готові відповіді на границі і сьогодні зупинимося лише на випадку, коли змінна в функції чи номер в послідовності прямує до нескінченності. Методика обчислення границь функцій на нескінченності наведена раніше, тут лише зупинимося на окремих випадках, які не є всім очевидними та простими.
Приклад 35. Маємо послідовність у вигляді дробу, де в чисельнику і знаменнику є кореневі функції. Потрібно знайти границю при номері, прямуючому до нескінченності.
Тут розкривати ірраціональності в чисельнику не потрібно, а лише уважно проаналізувати корені та знайти де міститься номер в найвищому степені.
В першому корені чисельника маємо множником n^4, тобто n^2 можемо винести за дужки. Теж саме проробимо із знаменником.
Далі оцінюємо значення підкореневих виразів при граничному переході.
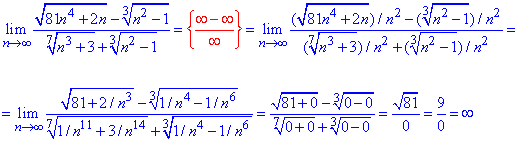
Отримали ділення на нуль, що є неправильно в шкільному курсі, проте в граничному переході це допустимо.
Лише з поправкою, "щоб оцінити куди прямує функція".
Тому наведений запис не всі викладачі можуть трактувати за правильний, хоча і розуміють, що результуюча границя від того не зміниться.
Давайте розглянемо відповідь, виконану за вимогами викладачів та теорією. Для спрощення оцінимо тільки головні доданкив під коренем
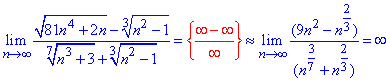
Далі в чисельнику степінь рівний 2, в знаменнику 2/3, отже чисельник швидше зростає, а значить границя прямує до безмежності.
Її знак залежить від множників при n^2, n^(2/3), тому вона додатна.
Приклад 36. Розглянемо приклад границі на частку показникових функцій. Таких прикладів на практичних розглядається мало, тому не всі студенти із легкістю бачать, як розкривати невизначеності.
Максимальний множник для чисельника і знаменника рівний 8^n, на нього і спрощуємо
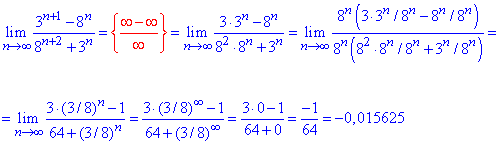
Далі оцінюємо вклад кожного доданку
Тут 3/8 прямує до нуля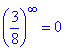 
при змінній прямуючій до безмежності, оскільки 3/8<1 (властивість степенево-показникової функції).
Приклад 37. Границя послідовності з факторіалами розкривається розписанням факторіалу до найбільшого спільного множника для чисельника та знаменника.
Далі на нього спрощуємо та оцінюємо ліміт за значенням показників номера в чисельнику та знаменнику. В нашому випадку знаменник швидше зростає, тому границя рівна нулю.
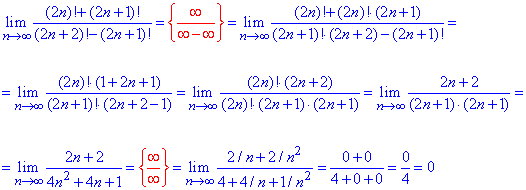
Тут використана наступна
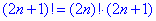
властивість факторіала.
Приклад 38. Не застосовуючи правила Лопіталя порівнюємо максимальні показники змінної в чисельнику та знаменнику дробу. Так як знаменник містить старший степінь 4>2 то і зростає він швидше. Звідси робимо висновок, що границя прямує до нуля.
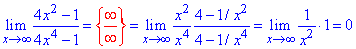
Приклад 39. Розкриваємо невизначенєсть виду безмежність розділити на безмежність винесенням x^4 із чисельника та знаменника дробу. В результаті границя рівна безмежності.
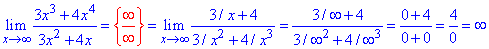
Приклад 40. Маємо частку поліномів, границя невизначена при змінній прямуючій до нескінченності.
Найстарший степінь змінної в чисельнику і знаменнику рівний 3, це значить що границя існує.
Винесемо x^3 та виконаємо граничний перехід
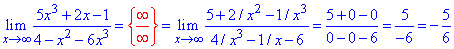
Приклад 41. Маємо особливість типу одиниця в степені безмежність. А це значить, що вираз в дужках і сам показник треба звести під другу важливу границю.
Розпишемо чисельник, щоб виділити в ньому вираз ідентичний знаменнику. Далі переходимо до виразу, який містить одиницю плюс доданок.
В степні потрібно виділити множником 1/(доданок). Таким чином отримаємо експоненту в степені границі дробової функції.
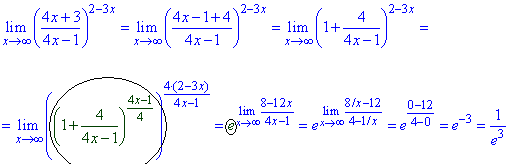
Тут використали другу важливу границю:
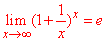
Приклад 42. Маємо особливість типу одиниця в степені безмежність.
Для її розкриття слід звести функцію під другу важливу границю. Як це зробити детально показано в наведеній далі формулі
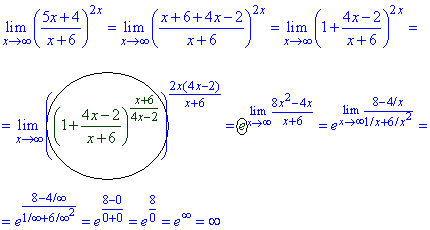
Подібних завдань Ви можете знайти надзвичайно багато. Їх суть, щоб в показнику отримати потрібний степінь, а він рівний оберненому значенню доданка в дужках при одиниці.
Таким методом отримуємо експоненту. Подальше обчислення зводиться до відшукання границі степені експоненти.
Тут експоненціальна функція прямує до нескінченності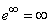 
, оскільки значення більше одиниці e=2.72>1.
Приклад 43 В знаменнику дробу маємо невизначеність типу безмежність мінус безмежність, що фактично рівне діленню на нуль. Щоб позбутися кореня домножимо на спряжений вираз, а далі за формулою різниці квадратів перепишемо знаменник. Отримаємо невизначеність безмежність розділити на безмежність, тому виносимо змінну в найбільшому степені та скорочуємо на неї. Далі оцінюємо вклад кожного доданку та знаходимо границю функції на нескінченності
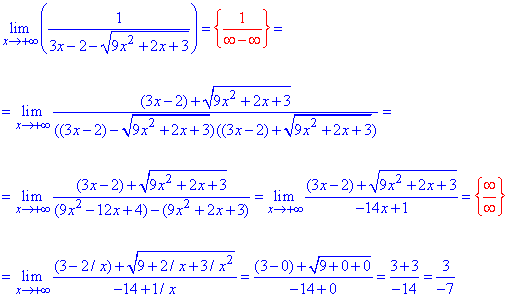
Приклад 44. Знайти повторні границі
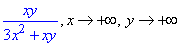
Розв'язання: Обчислюємо границю функції двох змінних спершу за y, а далі – x)
a)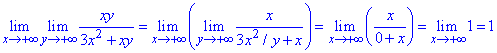
б)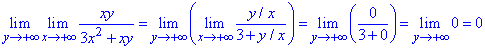 
Приклад 45. Обчислити повторні границі
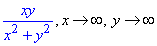
Розв'язання: Методика обчислення повторних границь не складна:
спершу знаходимо границю за однією змінною, вважаючи другу змінну сталою.
Далі лишається функція від однієї змінної, а таких границь ми розібрали чимало.
а)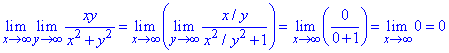 
б)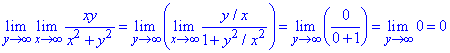 
В цьому завданні границі по першій змінній рівні нулю, тому повторні записуємо лише для формальності. Границя в даному завданні від порядку знаходження не залежить і рівна нулю.
Однак, якщо глянути відповідь з попереднього прикладу то таке твердження не завжди виконується.
Шукайте ефективні схеми обчислення границь на сторінках сайту, якщо маєте труднощі з границями на екзаменах та модулях - звертайтеся за допомогою!
