Задачі на знаходження границі функції дуже часто можна зустріти в таких науках як механіка, фізика, вища математика, прикладна математика і т.д. Суть таких задач полягає у відшуканні значення функції f(x) при прямуванні аргумента x до деякого значення x0, при якому функція може бути і невизначена. Поведінка функції в певній точці x0 і називається її границею. Вона може приймати як стале значення так і бути рівною безмежності (
).
ОЗНАЧЕННЯ ГРАНИЦІ
Нехай маємо функцію f(x), яка визначена в деякому околі X точки x0. Число A називається границею функції f(x) при прямуванні змінної до граничної точки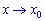 
, якщо для будь-якого малого наперед заданого додатнього числа 
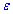можна знайти таке додатнє число 
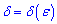, що для всіх змінних з окол 
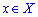, які задовільняють нерівність
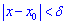
виконується нерівність
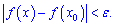
В спрощеній формі означення записують так
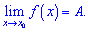
При 
функціяf(x)є нескінченно великою, якщо для довільного числа M>0 можна знайти таке число N=N(M), що для всіх змінних x, які задовільняють нерівність |x|>N, справджується нерівність |f(x)|>M.
В короткій формі дане означення прийме вигляд
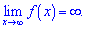
Функція g(x) є нескінченно малою при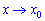 
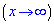, якщо виконується умова
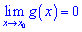
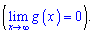
ОДНОСТОРОННІ ГРАНИЦІ
Запис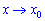 
можна розуміти, як наближення до точки x0 зліва, коли 
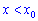і справа, коли x>x0. Таким чином, наближення точок x до x0 може бути двостороннім. На основі цього введені означення правої та лівої границі.
Число A є границею функції f(x) зліва (лівою границею), якщо для будь-якого числа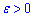 
існує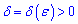 
таке, що при 
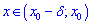виконується нерівність
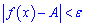
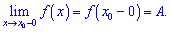
Число B є границею функції f(x) справа (правою границею), якщо для як завгодно малого значення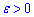 
знайдеться 
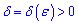таке, що для всіх x з проміжку 
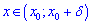виконується нерівність
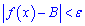
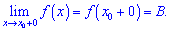
Ліва і права границі називаються одностороннніми границями.
Функція f(x) має границю в точці x0 тоді і тільки тоді, коли існують одночасно границі справа та зліва та вони рівні між собою
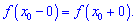
Розглянемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на знаходження границь.
Приклади. Знайти границі функцій
1) (4. 331)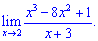 
Розв'язок. Перший приклад не є складними і розв'язування зводиться до підстановки значення аргумента у функцію
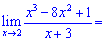
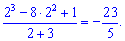
Це найпростіший тип границь, які по великому рахунку і границями важко назвати.
2) (4. 333)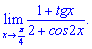 
Розв'язок. Як і в попередньому завданні, проводимо підстановку точки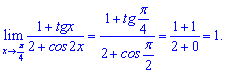
Тригонометричні функції при обчисленні границь теж потрібно знати.
3) (4. 337)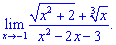 
Розв'язок. Спробуємо виконати підстановку змінної
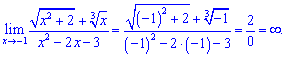
Знаменник прямує до нуля, тому границя рівна безмежності.
4) (4. 342)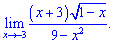 
Розв'язок. В такого типу прикладах потрібно знаменник розкласти за правилом різниці квадратів, після цього виконати підстановку. Доданок (3+х) спроститься і таким чином позбудемося особливості типу 0/0
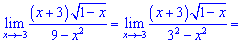
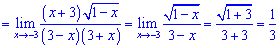
Таких прикладів попереду багато, схема розкриття особливості від прикладу до прикладу мало змінюється. Головне бачити до якого типу віднести границю функції.
5) (4. 348)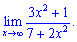 
Розв'язок. В функції потрібно чисельник і знаменник скоротити на множник, який вносить найбільший вклад
д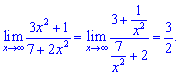
Тут не важко здогадатися, що ним буде квадрат змінної.
6) (4. 357)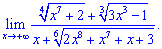 
Розв'язок. В такого сорту прикладах шукають найбільший показник змінної в чисельнику та знаменнику, а вже потім проводять аналіз. При прямуванні змінної до безмежності 
корені поводитимуть себе наступним чином
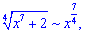
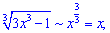
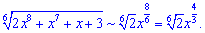
З оцінки показників бачимо, що чисельник швидше зростає ніж знаменник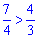 
отже функція є нескінченно великою
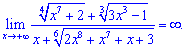
Границя рівна безмежності.
На цьому ввідний урок знаходження границь функцій завершено. Інші приклади обчислення границь та методику їх знаходження Ви знайдете в наступних матеріалах.
Переглянути подібні матеріали
