Теория пределов - один из разделов математического анализа, который одним под силу освоить, другие с трудом вычисляют пределы. Вопрос нахождения пределов является достаточно общим, поскольку существуют десятки приемов решения пределов различных видов. Одни и те же предела можно найти как по правилу Лопиталя, так и без него. Бывает, что расписание в ряд бесконечно малых функций позволяет быстро получить нужный результат. Существуют набор приемов и хитростей, позволяющих найти предел функции любой сложности. В данной статье попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике. Теорию и определение предела мы здесь давать не будем, в интернете множество ресурсов где это разжевано. Поэтому займемся практическим вычислениям, именно здесь у Вас и начинается "не знаю! Не умею! Нас не учили!"
Вычисление пределов методом подстановки
Пример 1. Найти предел функции
Lim((x^2-3*x)/(2*x+5),x=3).
Решение: Такого сорта примеры по теории вычисляют обычной подстановкой
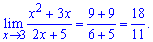
Предел равен 18/11.
Ничего сложного и мудрого в таких пределах нет - подставили значение, вычислили, записали предел в ответ. Однако на базе таких пределов всех приучают, что прежде всего нужно подставить значение в функцию. Далее пределы усложняют, вводят понятие бесконечности, неопределенности и тому подобные.
Предел с неопределенностью типа бесконечность разделить на бесконечность. Методы раскрытия неопределенности
Пример 2. Найти предел функции
Lim((x^2+2x)/(4x^2+3x-4),x=infinity).
Решение: Задан предел вида полином разделить на полином, причем переменная стремится к бесконечности
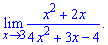
Простая подстановка значения к которому следует переменная найти пределов не поможет, получаем неопределенность вида бесконечность разделить на бесконечность.
Пот теории пределов алгоритм вычисления предела заключается в нахождении наибольшего степени "икс" в числителе или знаменателе. Далее на него упрощают числитель и знаменатель и находят предел функции
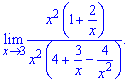
Поскольку значение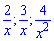 
стремятся к нулю при переменной к бесконечности то ими пренебрегают, или записывают в конечный выражение в виде нулей
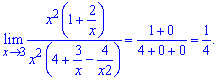
Сразу из практики можно получить два вывода которые являются подсказкой в вычислениях. Если переменная стремится к бесконечности и степень числителя больше от степени знаменателя то предел равен бесконечности. В противном случае, если полином в знаменателе старшего порядка чем в числителе предел равен нулю.
Формулами предел можно записать так
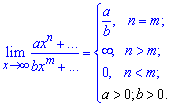
Если имеем функцию вида обычный поленом без дробей то ее предел равен бесконечности
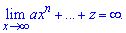
Следующий тип пределов касается поведения функций возле нуля.
Пример 3. Найти предел функции
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Решение: Здесь уже выносить старший множитель полинома не требуется. С точностью до наоборот, необходимо найти наименьший степень числителя и знаменателя и вычислить предел
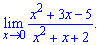
Значение x^2; x стремятся к нулю когда переменная стремится к нулю 
Поэтому ими пренебрегают, таким образом получим
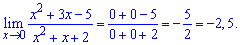
что предел равен 2,5.
Теперь Вы знаете как найти предел функции вида полином разделить на полином если переменная стремится к бесконечности или 0. Но это лишь небольшая и легкая часть примеров. Из следующего материала Вы научитесь как раскрывать неопределенности пределов функции.
Предел с неопределенностью типа 0/0 и методы его вычислений
Сразу все вспоминают правило согласно которому делить на ноль нельзя. Однако теория пределов в этом контексте подразумеваем бесконечно малые функции.
Рассмотрим для наглядности несколько примеров.
Пример 4. Найти предел функции
Lim((3x^2+10x+7)/(x+1), x=-1).
Решение: При подстановке в знаменатель значения переменной x = -1 получим ноль, то же самое получим в числителе. Итак имеем неопределенность вида 0/0.
Бороться с такой неопределенностью просто: нужно разложить полином на множители, а точнее выделить множитель, который превращает функцию в ноль.
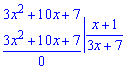
После разложения предел функции можно записать в виде
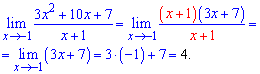
Вот и вся методика вычисления предела функции. Так же поступаем если есть предел вида многочлен разделить на многочлен.
Пример 5. Найти предел функции
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Решение: Прямая подстановка показывает
2*4-7*2+6=0;
3*4-2-10=0
что имеем неопределенность типа 0/0.
Разделим полиномы на множитель которій вносит особенность
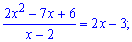
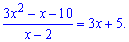
Есть преподаватели которые учат, что полиномы 2 порядка то есть вида "квадратные уравнения" следует решать через дискриминант. Но реальная практика показывает что это дольше и запутаннее, поэтому избавляйтесь особенности в пределах по указанному алгоритму. Таким образом записываем функцию в виде простых множителей и вічисляем в предел
Как видите, ничего сложного в исчислении таких пределов нет. Делить многочлены Вы на момент изучения пределов умеете, по крайней мере согласно программе должны уже пройти.
Среди задач на неопределенность типа 0/0 встречаются такие в которых нужно применять формулы сокращенного умножения. Но если Вы их не знаете, то делением многочлена на одночлен можно получить нужную формулу.
Пример 6. Найти предел функции
Lim((x^2-9)/(x-3), x=3).
Решение: Имеем неопределенность типа 0/0. В числителе применяем формулу сокращенного умножения
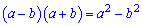
и вычисляем нужній предел
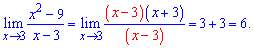
Метод раскрытия неопределенности умножением на сопряженное
Метод применяют к пределам в которіхнеопределенность порождают иррациональные функции. Числитель или знаменатель превращается в точке вычисления в ноль и неизвестно как найти границу.
Пример 7. Найти предел функции
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Решение: Представим переменную в формулу предела
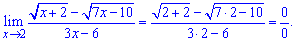
При подстановки получим неопределенность типа 0/0.
Согласно теории пределов схема обхода данной особенности заключается в умножении иррационального выражения на сопряженное. Чтобы выражение не изменилось знаменатель нужно разделить на такое же значение
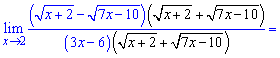
По правилу разности квадратов упрощаем числитель и вычисляем предел функции
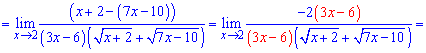
Упрощаем слагаемые, создающие особенность в пределе и выполняем подстановку
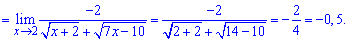
Пример 8. Найти предел функции
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Решение: Прямая подстановка показывает что предел имеет особенность вида 0/0.
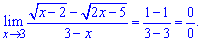
Для раскрытия умножаем и делим на сопряженное к числителю
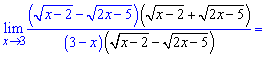
Записываем разницу квадратов
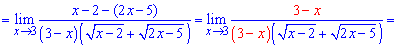
Упрощаем слагаемые которые вносят особенность и находим предел функции
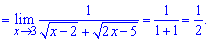
Пример 9. Найти предел функции
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Решение: Подставим двойку в формулу
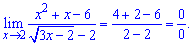
Получим неопределенность 0/0.
Знаменатель нужно умножить на сопряженный выражение, а в числителе решить квадратное уравнение или разложить на множители, учитывая особенность. Поскольку известно, что 2 является корнем, то второй корень находим по теореме Виета
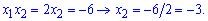
Таким образом числитель запишем в виде
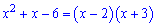
и подставим в предел
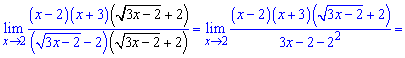
Сведя разницу квадратов избавляемся особенности в числителе и знаменателе
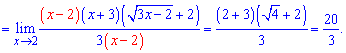
Приведенным образом можно избавиться особенности во многих примерах, а применение надо замечать везде где заданная разница корней превращается в ноль при подстановке. Другие типы пределов касаются показательных функций, бесконечно малых функций, логарифмов, особых пределов и других методик. Но об этом Вы сможете прочитать в перечисленных ниже статьях о пределах.
Вычисления пределов в Мейпл
Данный материал полезен прежде всего для студентов. Возможно в программе обучения, а некоторые для себя изучает математические программы для облегчения обучения и проверки решений. Это могут быть математические пакеты MathСad, Мathematica, Maple. Вычисления пределов в Мейпл достаточно просто организовать даже новичку. Все что нужно - правильно ввести функцию предел которой находим.
> restart;
Предел первой функции из тех которые рассматривали в Мейпл иметь следующую запись. Жмем конце "Enter" и получим конечное значение пределов
> limit((x^2+3*x)/(2*x+5),x=3);
18/11
Предел второй функции получим из записи
> limit((x^2+2*x)/(4*x^2+3*x-4),x=infinity);
1/4
Третий пример примет следующий вид:
> limit((x^2+3*x-5)/(x^2+x+2),x=infinity);
1
Мэйпл без проблем находит первый замечательный предел
> limit(sin(x)/x,x=0);
1
и второй замечательный предел
> limit((1+1/x)^x,x=infinity);
exp(1).
Фрагмент вычисления пределов в математическом пакете Мэйпл приведен ниже
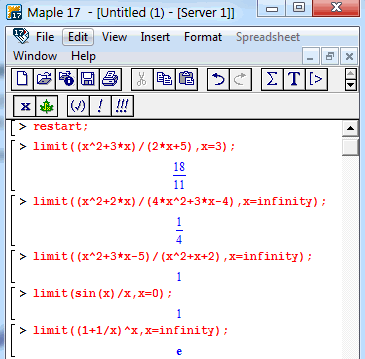
С Мейплом Вы без труда найдете предел логарифма, тригонометрических, экспоненциальных и других функций.
Похожие материалы:
