Задачі на знаходження границі числових послідовностей при прямуванні номера їх загального члена до безмежності займають важливе місце в вищій математиці та можуть багато розказати про їх збіжність.
Основна суть в знаходженні таких границь полягає у виділенні із чисельника та знаменника найбільшого доданка чи множника. Після цього чисельник і знаменник ділять на це значення та отримують кінцевий результат.
Розглянемо задачі із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Знайти границі.
1) (4. 285)
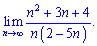
Розв'язок. В чисельнику і знаменнику виділяємо множник, який вносить найбільший вклад та скорочуємо на нього
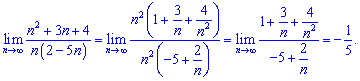
Д альше в дужках чисельника і знаменника бачимо домінуючі доданки, які і складають границю числової послідовності.
2) (4. 291)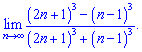 
Розв'язок. Виділяємо множники, що містять третю степінь і скорочуємо на них
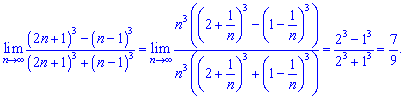
В підсумку записуємо ті додани, що внесуть вклад в границю послідовності.
3) (4. 293)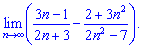 
Розв'язок. Розбиваємо даний приклад на суму двох границь, за правилами маємо право на це. Далі в кожній з границь виносимо в чисельнику та знаменнику домінючі множники за дужки
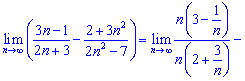
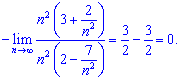
В результаті прийдемо до того, що границі рівні, оже їхня різниця - нуль.
4) (4. 295)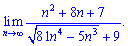 
Розв'язок. В такого типу прикладах потрібно винести в знамениику з під кореня множник в найбільшому степені. Як це зробити - перемножити показники 4*(1/2)=2
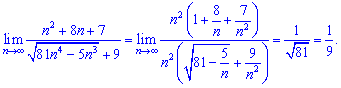
Далі приходимо до частки, яка в підсумку дає limit=1/9.
5) (4. 298)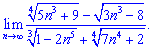 
Розв'язок. В цьому завданні та подібних потрібно знайти доданок з максимальним степенем
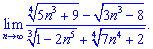
В чисельнику змінна n знаходиться в степенях 3/4 та 1/3. Змінна в знаменика є в степенях 5/3 та 1. Оскільки найбільший степінь знаменника 5/3 є більшим від степені чисельника 3/4, то знаменник зростатиме швидше ніж чисельник. В такому випадку границя послідовності рівна нулю
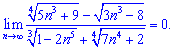
Якщо б було навпаки, то границя була б рівна нескінченності (
). У випадку однакових показників змінної, чисельник і знаменник скорочуємо на неї та отримуємо константу.
6)(4. 301)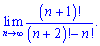 
Розв'язок. Границі з факторіалами займають особливе місце серед числових послідовностей. При їх знаходженні чисельник і знаменник розкладають до найбільшого спільного факторіалу
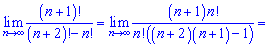
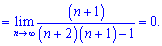
Даі спрощують спільні множники та аналізують швидкості зростання чи спадання послідовності. Границя рівна нулю, тому що степінь знаменника (2) більший від чисельника (1).
7) (4. 302)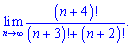 
Розв'язок. Як і у попередньому прикладі розкладаємо до найбільшого спільного факторіалу
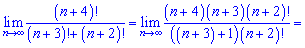
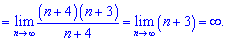
Тут картина протилежна - чисельник зростає квадратично, знаменник лінійно, тому границя послідовності прямує до безмежності.
8) (4. 304)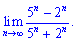 
Розв'язок. До прикладів, в яких змінна n виступає в ролі показника треба ставитися з особливою увагою. Незнання закономірностей поведінки степеневих функцій часто приводить до помилок в розв'язуванні. В даному прикладі 5n зростає значно швидше за 2n , тому його виділяємо як найбільший множник
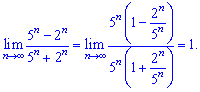
Далі бачимо, що двійа ніякого вкладу не вносить, а гриниця такої послідовності рівна одиниці.
9) (4. 307)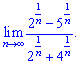 
Розв'язок.Числа в показникахі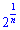
та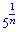 
прямують до одиниці (показники до нуля) при великих значеннях номера 
. На основі цього записуємо границю послідовності
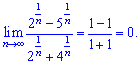
Подібних прикладів можна знайти чимало і розв'язування більшості з них полягає у знаходженні домінуючого множника. Якщо він у чисельнику то границя прямує до безмежності, у знаменнику – до нуля. І тільки коли найбільший множник присутній і там і там можна скоротити на цей множник дріб і отримати границю у вигляді константи. При факторіалах, числах в показниках схема виділення границі взагалі міняється, такі границі будуть детальніше розгляуті в наступних уроках.
