Знайти суму арифметичної прогресії

Переходимо до обчислень суми арифметичної прогресії, а для цього Вам потрібно знати наступні формули

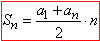
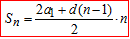
тут a₁, a_n та n члени арифметичної прогресії; d - різниця (крок) прогресії.
В 9, 10 класах школи Ви обчислювали прості завдання, тут Вам пропонуємо відповіді ЗНО тестів, а вірніше приклади, які гіпотетично можуть Вас чекати при зовнішньому незалежному оцінюванні. Всі решта із 45 прикладів розв'язані або на попередніх уроках, а бо чекають Вас дальше при вивченні геометричної прогресії та всього, що з нею пов'язано.

Приклад 21.5 В арифметичній прогресії тридцять членів.
Знайти суму всіх членів прогресії, якщо перший її член дорівнює -12, а останній – 75.

Обчислення: Маємо а/п, у якої n=30, a₁=-12, a₃₀=75.
Тоді її суму знаходиться за формулою:
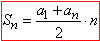 Маємо всі дані для обчислень, тож з легкістю розраховуємо

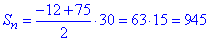
Відповідь: 945 – Б.

Приклад 21.6 Знайти суму перших тринадцяти членів арифметичної прогресії -8; -5; -2; …

Обчислення: Запишемо, що нам відомо з арифметичної прогресії а/м
n=13, a₁=-8, a₂=-5, a₃=-2, звідси знаходимо крок прогресії
d=a₂-a₁=-5-(-8)=3.
Суму арифметичної прогресії знаходимо за формулою:
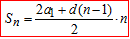 Обчислюємо

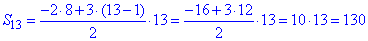
Відповідь: 130 – В.

Приклад 21.7 Третій і сьомий члени арифметичної прогресії відповідно дорівнюють 11 і 23.
Знайти суму 10-ти перших членів цієї прогресії.

Обчислення: Маємо а/п, у якої n=10, a₃=11, a₇=23.
Використаємо формулу a_n=a₁+d(n-1) для складання системи рівнянь, з якої знайдемо перший член та різницю прогресії:

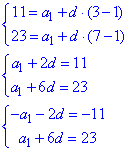
Такі системи рівнянь Ви повинні навчитися швидко складати та розв'язувати. Це одні з найпростіших завдань на прогресії, важчі розв'язуються через квадратні рівняння та виведення складних формул.
4d=12, d=3 - різниця а/п.
a₁=11-2d=11-2•3=5 - перший член а/п.
Обчислюємо суму 10-ти перших членів а/п

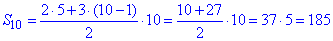
Відповідь: 185 – В.

Приклад 21.14 В арифметичній прогресії (a_n) a₈=6. Знайти S₁₅.

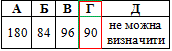
Обчислення: Відомий лише один член арифметичної прогресії a₈=6.
Використаємо формулу a_n=a₁+d(n-1) та розпишемо
a₈=a₁+d(8-1)=a₁+7d=6.
Для обчислення S₁₅ застосуємо відому формулу:

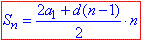
в якій в чисельнику виразимо вираз, лінійний до a₈

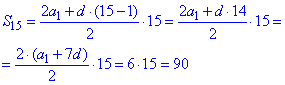
Відповідь: 90 – Г.

Приклад 21.16 (an) - арифметична прогресія.
Знайти суму перших її десяти членів, якщо a₄=10 , a₇=19.

Обчислення: В а/п відомі два члени a₄=10 і a₇=19.
З допомогою формули a_n=a₁+d(n-1) складаємо систему двох лінійних рівнянь для знаходження першого члена та різниці прогресії

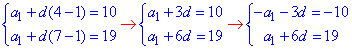
Просумувавши рівняння, отримаємо 3d=9, звідси d=3 - різниця а/п.
З першого рівняння обчислюємо a₁+3•3=10, a₁=1 - перший член а/п.
Для обчислення суми S₁₀ скористаємося формулою:

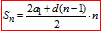
Підстановкою отримаємо S₁₀=145.

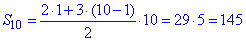
Відповідь: 145 – А.

Приклад 21.17 Знайти суму натуральних чисел від 40 до 200 включно.

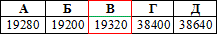
Обчислення: Оскільки маємо натуральні числа то між ними різниця рівна 1, а сама прогресія є арифметичною.
Визначаємо a₁=40, a_n=200 і n=200-40+1=161 - кількість членів а/п.
Для обчислення суми а/п використаємо формулу


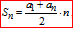
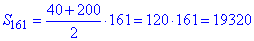
Відповідь: 19320 – В.

Приклад 21.27 Установити відповідність між арифметичними прогресіями (a_n) (1–4), заданими двома членами, та формулами сум n перших її членів (А – Д).

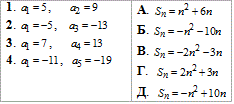
Обчислення: Із загальної формули
a_n=a₁+d(n-1)
виражаємо крок прогресії d=(an-a1)/(n-1).
А далі обчислюємо суму арифметичної прогресії за формулою:

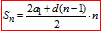
Ось такий простий алгоритм обчислень.
1) a₁=5, a₂=9
d=(9-5)/(2-1)=4, тоді

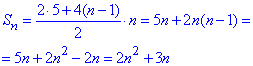
1 - Г.

2) a₁=-5, a₃=-13

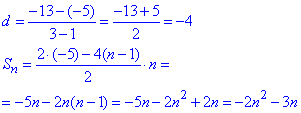
2 - В.

3) a₁=7, a₄=13
d=(13-7)/(4-1), тоді

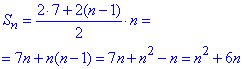
3 - А.

4) a₁=-11, a₅=-19

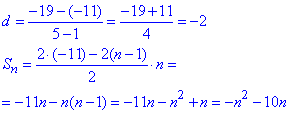
4 - Б.
Уважно перегляньте схему розв'язування прикладів.

Приклад 21.28 Установити відповідність між арифметичними прогресіями (a_n) (1–4), заданими двома членами, та сумами 10 перших її членів (А – Д).
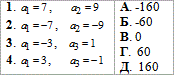 Обчислення: Як і для попередніх завдань, з формули
a_n=a₁+d(n-1).
виражаємо крок прогресії d=(a_n-a₁)/(n-1).
А далі знаходимо суму а/п за формулою:

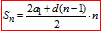
для n=10 вона матиме вигляд

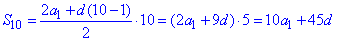
Її застосовуємо в наступних розрахунках.
1) a₁=7, a₂=9
d=a₂-a₁=9-2=7, тоді
S₁₀=10•7+45•2=70+90=160.
1 - Д.

2) a₁=-7, a₂=-9
d=a₂-a₁=-9-(-7)=-2, тоді
S₁₀=10(-7)+45(-2)=-160.
2 - А.

3) a₁=-3, a₃=1

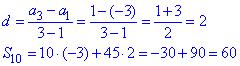
3 - Г.

4) a₁=3, a₃=-1

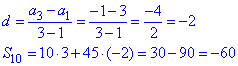
4 - Б.

Це класичні приклади, які Ви повинні вміти швидко розв'язувати. Далі наведемо ще два приклади складніших завдань на прогресію, які можуть розв'язати школярі та студенти з добрим аналітичним мисленням та підготовкою.

Приклад 21.37 Знайти суму S усіх трицифрових натуральних чисел, які діляться на число 7 без остачі.
У відповідь записати S:100.
Обчислення: Трицифрові числа, які діляться на число 7 (тобто кратні числу 7) утворюють арифметичну прогресію з різницею d=7.
a₁=105 - найменше трицифрове, яке ділиться на 7, a_n=994 - найбільше трицифрове, яке ділиться на 7.
Обчислимо кількість таких чисел за формулою:
a_n=a₁+d(n-1)
105+7(n-1)=994
105+7n-7=994
7n=896
n=128.
Загальна кількість трицифрових чисел, які кратні 7 дорівнює 128.
Суму цих чисел обчислюють за формулою а/п:

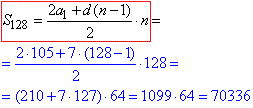
звідси S:100=703,36
Відповідь: 703,36.

Приклад 21.35a Знайти суму S членів арифметичної прогресії (a_n) з десятого до сорокового включно, якщо a₁=-10, d=2.
У відповідь записати S:100.
Обчислення: Маємо а/п, у якої a₁=-10, d=2.
Суму її перших n членів обчислюють за формулою:

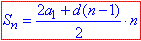
Схема наступна: знаходимо суму 40 членів, потім 9 членів прогресії.
Їх різниця S₄₀-S₉ і буде сумою від 10 до 40, яку потрібно знайти в умові.
Спочатку знайдемо суму S₉ дев'яти перших членів заданої а/п (n=9):

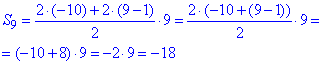
Тепер знайдемо суму S₄₀ сорока перших членів заданої а/п (n=40):

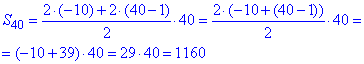
Суму S членів арифметичної прогресії (a_n) з десятого до сорокового включно знайдемо як різницю суми перших сорока членів і перших дев'яти членів заданої а/п, отже

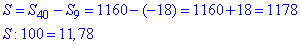
Відповідь: 11,78.

Думаю основні схеми обчислень та формули суми прогресії Ви запам'ятали. З базовими прикладами на суму прогресії ми Вас познайомили, хто бажає переглянути всі завдання із ЗНО тестів то переходіть в право на наступні уроки поки не побачити прикладів з номерами 44, 45,...
Далі переходимо до геометричних прогресій, обчислення знаменника, членів геометричної прогресії та сум.

Вас може зацікавити:
1. Сума арифметичної прогресії. 9 клас
2. Геометична прогресія, сума геометричної прогресії
3. Арифметична прогресія. ЗНО
4. Арифметична прогресія. Формули та приклади