Подвійні та потрійні інтеграли

Подвійні та потрійні інтеграли даються важко усім студентам. Одна з причин - це відсутність можливості якісно будувати області інтегрування. З уяви їх брати вдається не багатьом фахівцям. Що стосується знаходження об'ємів, утворених перетином площин, то тут ця проблема вилазить ще більше. Інша справа, що часто кратні інтеграли починають вивчати коли студенти тільки но так-сяк навчилися знаходити визначені інтеграли. Усім Вам допоможуть в навчанні готові відповіді індивідуальної роботи. Наведених 10 прикладів навчать Вас вирішувати завдання любої складності.

ВАРІАНТ – 19

Подвійний інтеграл

Приклад 1.14 Поміняти порядок інтегрування в подвійному інтегралі:

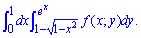
Розв'язання: З інтегралу виписуємо область інтегрування, яка обмежена кривими

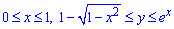
де 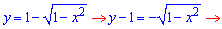(y-1)²=1-x², x²+(y-1)²=1.
Отримали нижнє півколо з центром у точці O(0;1) і радіусом R=1.
Виразимо отримані функції через змінну y:
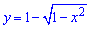, звідси 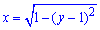перед радикалом стоїть знак «+» оскільки частина кола знаходиться у правій (додатній по x) частині півплощини;
y=e^x, звідси x=ln(y).
Виконуємо побудову рисунка до задачі, це слугує доброю підказкою при виконанні завдань

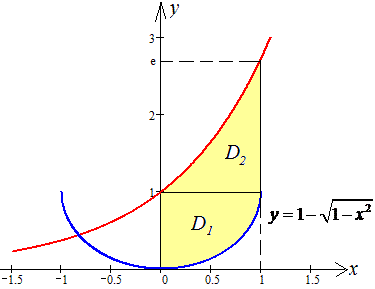
Як змінювати межі інтегрування Вас мабуть вчили. Якщо не всі знають, то просто уявно проведіть пряму та випишіть закон за яким змінюються краї при проходженні кривої знизу вгору, чи зліва направо. Таким чином Ви будете знати і кількість областей розбиття, і функції, що обмежують площу чи об'єм тіла.
При зміні порядку інтегрування нашу область розбили на дві області: D=D₁+D₂.
Розставимо межі в кожній області:

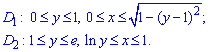
Ще раз уважно перегляньте малюнок, та спробуйте проаналізувати чому так.
При зміні меж інтегрування отримаємо два подвійні інтеграли
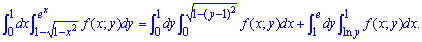На цьому і всі пояснення до першої задачі.

Приклад 2.13 Знайти площу плоскої фігури, заданої наступними умовами: xy=1, xy=2, 6y=7-x.
Розв'язання: Спершу виконуємо побудову кривих, щоб зрозуміти площу якої фігури шукаємо

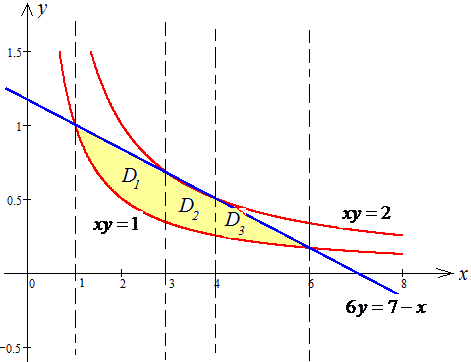
Далі бачимо, що область інтегрування потрібно розбивати на три частини.
Є інший варіант, легший з точки зору практичної реалізації. Можна знайти площу між двома червоними кривими і від неї відняти площу в області D₂ між червоною та синьою кривими. В результаті отримаємо різницю двох подвійних інтегралів. Але тут підемо довшим шляхом, описаний спробуйте реалізувати самостійно.
Перше, що нам потрібно - це визначити в яких точках графіку криві перетинають одна одну.
Знайдемо точки перетину графіків 1-ї та 3-ї функцій: складаємо систему із двох рівнянь

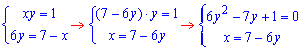
та знаходимо розв'язки

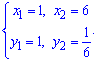
Перетин другої та третьої функцій дають систему рівнянь

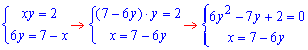
для визначення двох точок

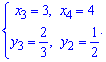
Таким , задану область будемо розбивати на три області: D=D₁+D₂+D₃.
Розставимо межі в кожній області:

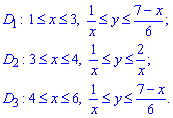
Через подвійний інтеграл обчислюємо площу фігури, обмеженої заданими кривими:
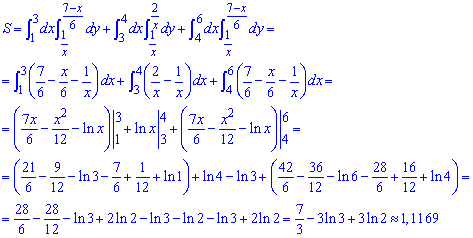Інтеграл в підсумку дає багато логарифмів, які групуємо. Наближено площа поверхні рівна 1,12 одиниць квадратних.

Приклад 3.12 Обчислити подвійний інтеграл по області D, обмеженій вказаними лініями: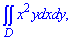
D: y=2x³, y=0, x=1.
Розв'язання: Знайдемо точки перетину графіків заданих функцій: 2x³=0, x=0.
Зобразимо графічно область інтегрування

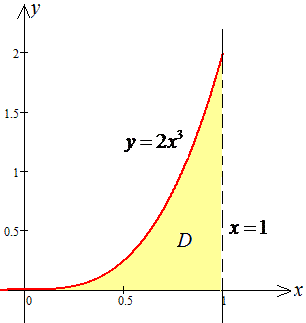
Розставимо межі в заданій області D:

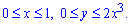
Обчислимо подвійний інтеграл по області D, обмеженій вказаними лініями: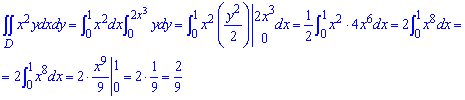
Нагадаємо, о це є лише подвійний інтеграл. Площа має місце лише у випадках, коли функція інтегрування рівна одиниці.

Приклад 4.11 Обчислити подвійний інтеграл, використовуючи полярні координати:

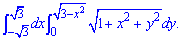
Розв'язання: Запишемо область інтегрування, яка обмежена кривими

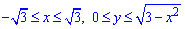
де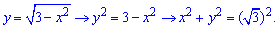
Отримали коло з центром у точці O(0;0) і радіусом рівним кореню з трьох 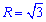(верхня половина).
Зобразимо півколо в декартовій та полярній системі координат

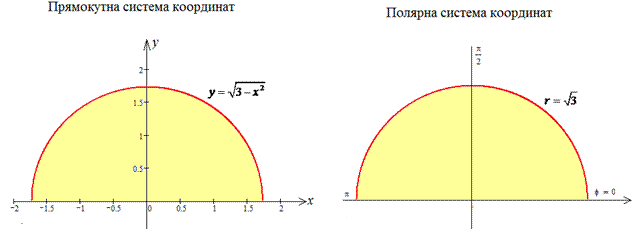
Перейдемо до полярної системи координат (СК), використовуючи наступну заміну змінних:

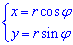
Слід пам'ятати, о додатково потрібно обчислити якобіан переходу від декартової до полярної СК:

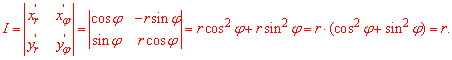
Він важливий, оскільки на нього потрібно домножити підінтегральну функцію, виражену в нових координатах
Знайдемо вигляд підінтегральної функції в полярній системі координат:

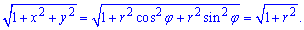
Запишемо межі інтегрування в полярній СК:

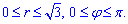
Залишилося обчислити подвійний інтеграл:

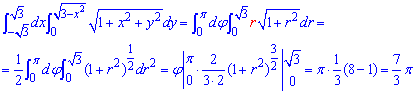
Інтеграл рівний I=7*Pi/3. Те, що інтеграл містить число Pi лише підтверджує правильність обчислень, адже для кругових форм це поширено.

Приклад 5.10 Обчислити площу області D, обмеженої вказаними лініями:
D: y=x2+2, x=2, y=x,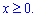

Розв'язання: Розставимо межі в заданій області D:

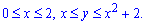
Побудуємо криві, щоб уявити площу чого ми шукаємо.

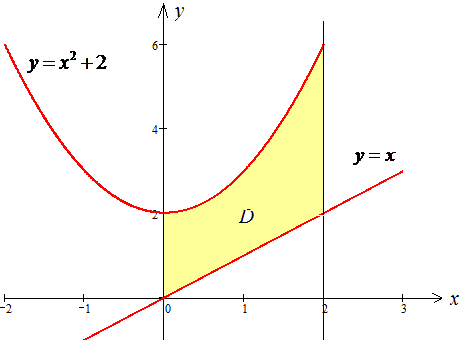
Тут є два варіанти: складний - коли внутрішній інтеграл за змінною x передбачає знаходження площі, через суму подвійних інтегралів за 2 або 3 областями. Ми ж підемо легким шляхом і визначимо площу заштрихованої фігури за допомогою одного подвійного інтегралу.
Обчислимо площу криволінійної трапеції, обмеженої вказаними лініями: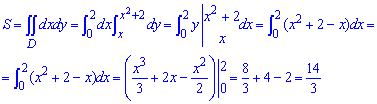
Площа рівна S=14/3 одиниць квадратних.
Як бачите - вибір порядку інтегрування може суттєво зекономити час при написанні контрольної роботи, на екзамені чи практичних завданнях. Для порівняння спробуйте обчислити першим часом та порівняти масштаб виконаних робіт.

  Приклад 6.9 Використовуючи подвійний інтеграл, обчислити, перейшовши до полярних координат, площу плоскої фігури: (x²+y²)²=a²(2x²+3y²).
Розв'язання: Один з попередніх прикладів містив перехід до полярної системи координат:

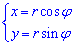
і був знайдений якобіан переходу I=r.
Визначимо межі інтегрування:

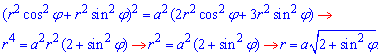
Отож, маємо межі: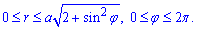

Їх легко визначити в полярній СК - радіус змінюється від нуля до кривої, що обмежує площу, а кут змінюється від 0 до 360 градусів. Це Ви повинні знати при обчисленні подібних завдань.
Обчислимо площу плоскої фігури:
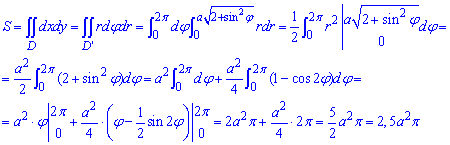Під інтегралом довелось понижувати степінь синуса за відомою тригонометричною формулою. На практиці Ви такі випадки розглядали, то ж тут ми Вам нічого нового не відкриваємо.

Приклад 7.8 Знайти об'єм тіла, заданого поверхнями, що його обмежують:
y=7-x²-z², 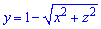, y=0.
Розв'язання: Половина 3D рисунку тіла зобразимо графічно - це хороша підказка, що розвиває уяву.

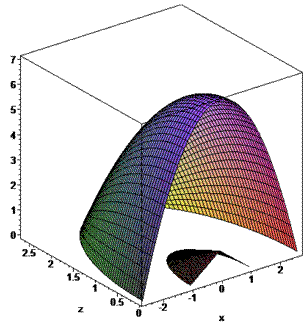
Обчислимо об'єм тіла, що обмежує ці дві поверхні (тобто рисунок розрізали навпіл для наочного відображення) знизу площиною y=0.
Щоб спростити інтеграли об'єм тіла знайдемо як різницю об'ємів параболоїда і конуса (див. рис.).

Розставимо межі в заданій області D₁ (коло радіусом ):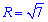

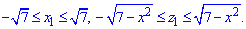
Знайдемо об'єм параболоїда:

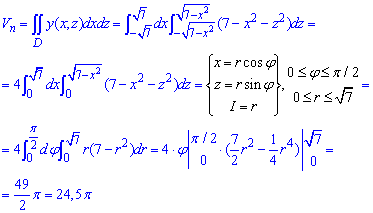
При знаходженні подвійного інтегралу доцільно перейти до полярної СК, оскільки обидві фігури утворені обертанням кривої навколо осі Oy.
Розставимо межі в області D2 (коло радіусом R=1):

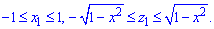
Обчислимо об'єм конуса:
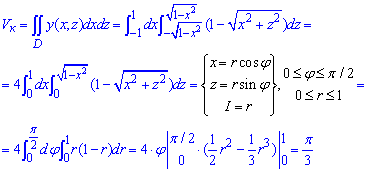Він рівний V=Pi/3 одиниць кубічних.
Тут також під час інтегрування перейшли до полярної СК.
Останнім кроком знайдемо об'єм тіла, що знаходиться між параболоїдом і конусом:
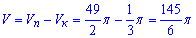Різниця об'ємів рівна V=145*Pi/6=75,88 одиниць кубічних.

Потрійний інтеграл

Приклад 8.7 Розставити межі інтегрування в потрійному інтегралі 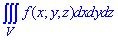, якщо область V обмежена вказаними поверхнями:
V: 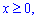y=2x, y=1, 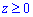,x+y+z=3.
Намалювати область інтегрування.
Розв'язання: В площині Oxy рівняння прямих запишемо наступним чином: y=1, x=y/2, x=3-y.
Рівняння площини в просторі запишемо у вигляді: z=3-y-x.
Побудуємо просторовий рисунок тіла та його проекцію в декартову площину

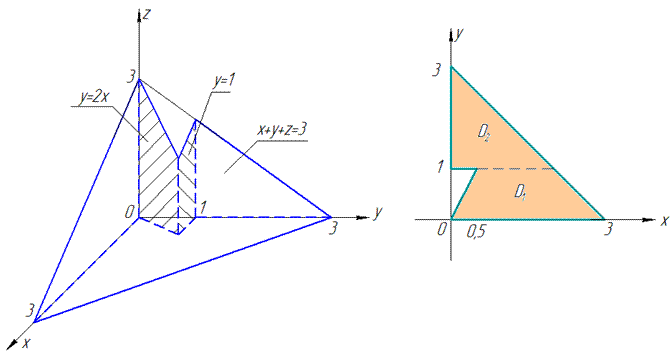
Як видно із рисунку область тіла D, що проектується на площину Oxy, розбивається на дві частини: D=D₁+D₂, тому межі інтегрування розставляємо наступним чином:

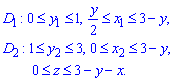
На основі проведеного аналізу записуємо межі в потрійному інтегралі
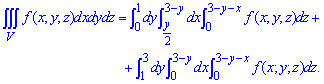Уважно розберіть як зміняться межі, якщо інтегрувати за змінною y у внутрішньому інтегралі. Легко переконатися, що отримаємо суму із трьох потрійних інтегралів.

.Приклад 9.6 Обчислити потрійні інтеграли: 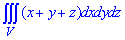де область інтегрування обмежена: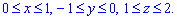
Розв'язання: Область являє собою паралелепіпед, який зображено нижче

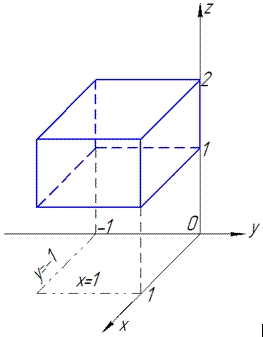
Це значно спрощує інтегрування
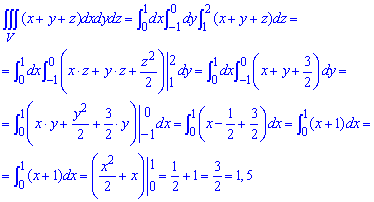Деталі обчислень добре розписані у формулах, тому тут важливо лише правильно підставити межі та не помилитися при сумуванні.

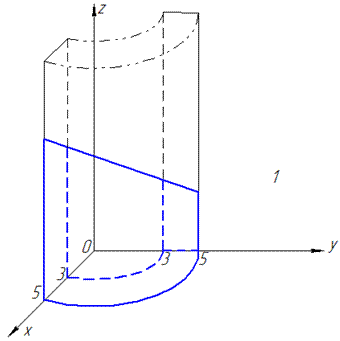
Приклад 10.5 Використовуючи потрійний інтеграл, обчислити об'єм тіла, обмеженого поверхнями: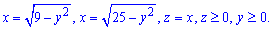
Намалювати область інтегрування.
Розв'язання: Перш за все виконуємо побудову до умови, в крайньому випадку старайтеся схематично намалювати область інтегрування

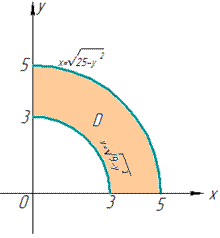
Далі записуємо межі інтегрування, враховуючи виконаний рисунок:

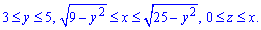
Через потрійний інтеграл знаходимо об'єм тіла:

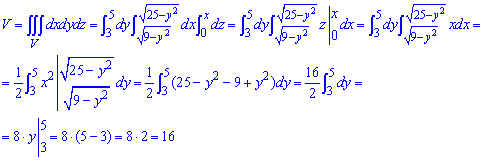
Перетворення не складні і їх розберіть самостійно.
Об'єм рівний 16 куб. од.
На цьому індивідуальну роботу з повторних інтегралів виконано. Більше прикладів на подвійні та потрійні інтеграли Ви можете знайти в наступних матеріалах.