Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
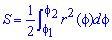 Задачи взяты из программы практикума для студентов мех-мата Львовского национального университета имени Ивана Франко. Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. "Практикум из математического анализа" (рядом стоит номер из сборника Б. П. Демидовича).
Задачи взяты из программы практикума для студентов мех-мата Львовского национального университета имени Ивана Франко. Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. "Практикум из математического анализа" (рядом стоит номер из сборника Б. П. Демидовича).
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли - геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли
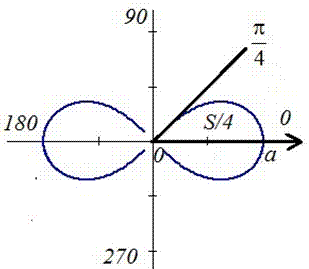
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
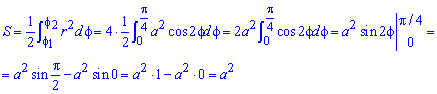
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) - кардиоида.
Вычисление: Кардиоида - плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
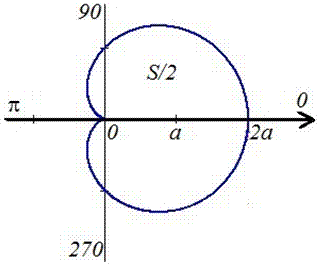
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
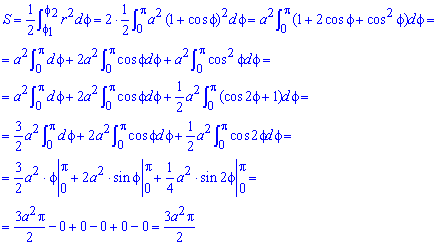
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
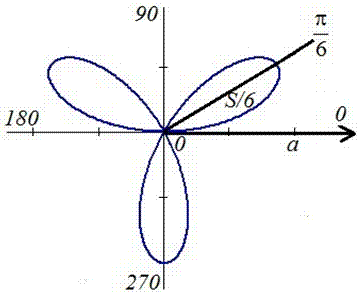
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
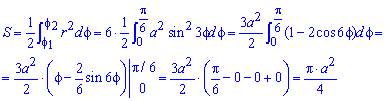
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 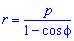 (парабола), f1=p/4, f2=p/2.
(парабола), f1=p/4, f2=p/2.
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
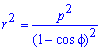
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
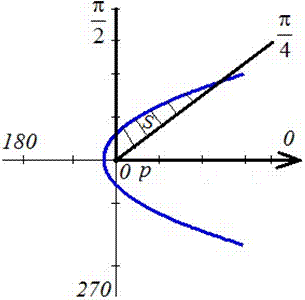
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
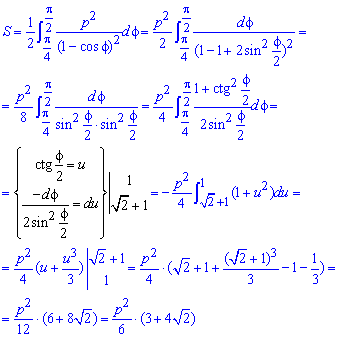
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 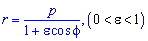 (эллипс)
(эллипс)
Вычисление: Запишем подинтегральную функцию:
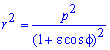
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
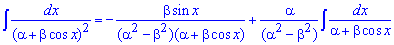
При выведении этой формулы пользовались методом интегрирования частями!
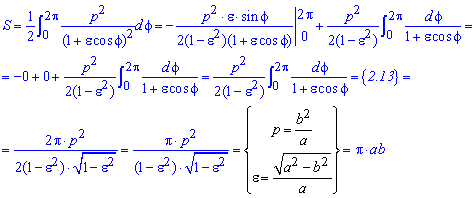
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
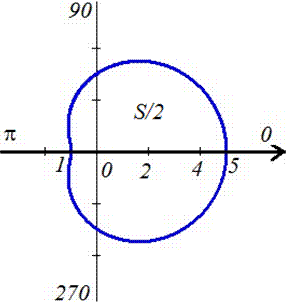
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
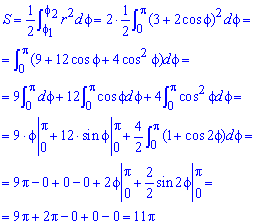
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
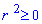 , поэтому
, поэтому 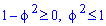 , откуда
, откуда 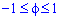 .
.
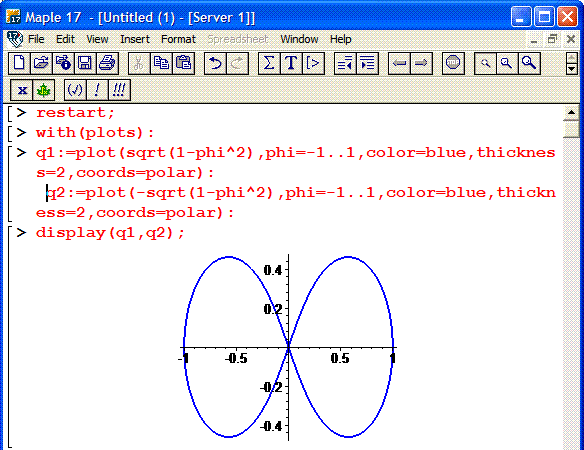
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
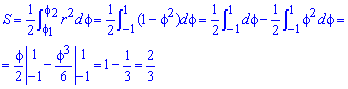
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми 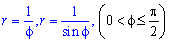 .
.
Вычисление: Выписываем подинтегральные функции:
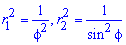
Поскольку на промежутке интегрирования 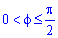 между кривыми выполняется неравенство
между кривыми выполняется неравенство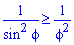 , то для нахождения площади имеем r22-r12.
, то для нахождения площади имеем r22-r12.
Найдем пределы интегрирования: f1=0 - особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
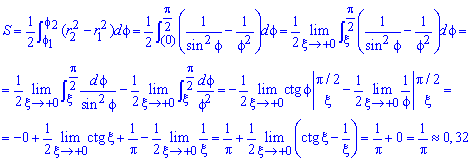
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой 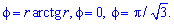
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
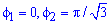 (известны за условием).
(известны за условием).
График функций имеет вид
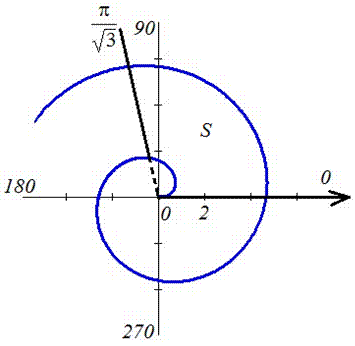
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
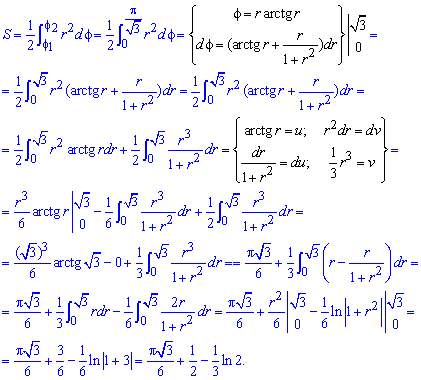
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.115 (2424.3) Найти площадь фигуры, ограниченной кривыми f=4r-r3, f=0.
Вычисление: Запишем подинтегральную функцию: r2.
Ее график в полярной системе координат имеет вид
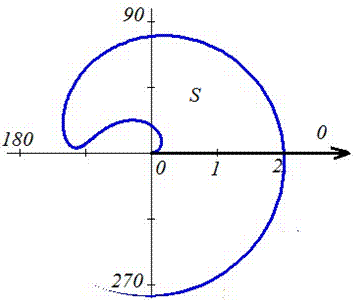
Установим пределы интегрирования: При росте r от 0 к 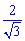 угол растет, при росте r от
угол растет, при росте r от 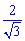 к 2 угол спадает, поэтому величина интеграла в пределах
к 2 угол спадает, поэтому величина интеграла в пределах 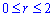 имеет знак "минус".
имеет знак "минус".
Вычислим площадь фигуры интегрированием: при этом найдем дифференциал по углу и перейдем к интегрированию по радиусу:
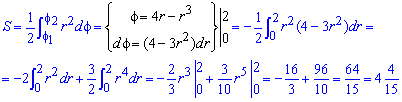
Перед интегралом (после замены переменных) поставили знак "минус", поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть больше нуля.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
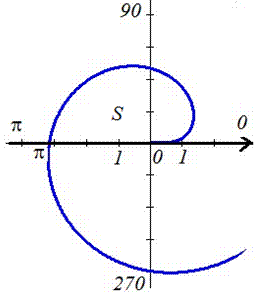
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
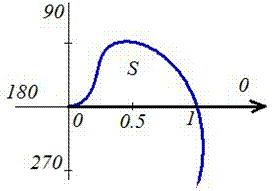
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
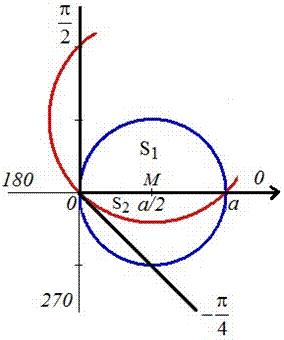
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
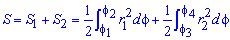
Записываем уравнение подинтегральных функций:
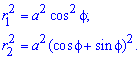
Определяем пределы интегрирования:
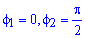 , где
, где 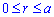 и
и 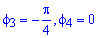 где
где 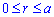 (точки пересечения линий).
(точки пересечения линий).
Вычисляем площадь изображенной фигуры интегрированием
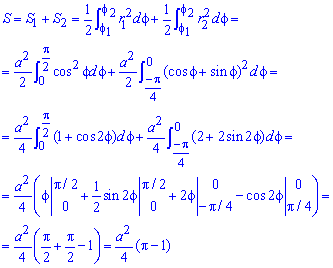
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак "минус".
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
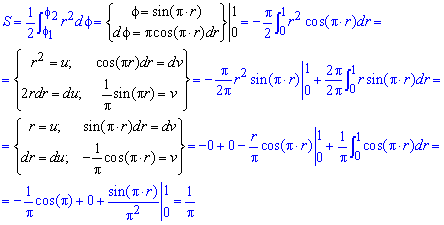
Перед интегралом (после замены переменных) поставили знак "минус", поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Пример 2425 Найти площадь фигуры, ограниченной кривой в полярной системе координат, заданной параметрически
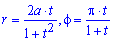
Вычисление: Складываем выражение для подинтегральной функции и дифференциал угла:
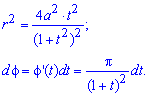
Устанавливаем пределы интегрирования по параметру:
Поскольку 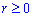
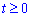 : r=0 при t=0 и
: r=0 при t=0 и  при
при 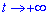 , поэтому имеем пределы интегрирования от нуля к бесконечности
, поэтому имеем пределы интегрирования от нуля к бесконечности 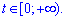
График кривой имеет вид.
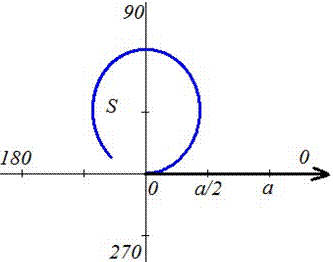
Вычислим площадь приведенной фигуры:
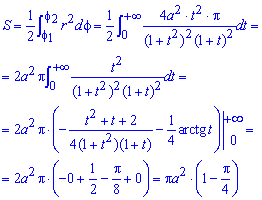
При интегрировании параметрической функции воспользовались методом Остроградського:
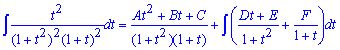
Возьмем производную от каждой части равенства и приравняем соответствующие коэффициенты:
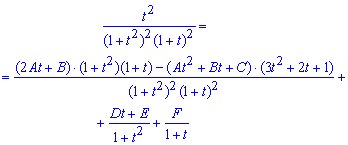
Отсюда A=-1/4; B=-1/4; C=-1/2; D=0;E=-1/4; F=0.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
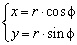
При подстановке в уравнение получим
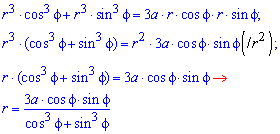
Поднесем к квадрату, чтобы получить подинтегральную функцию:
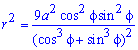
Выпишем пределы интегрирования:
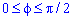 , потому что
, потому что 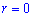 при
при 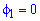 и при
и при 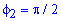 .
.
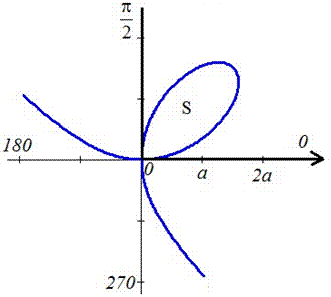
График функции имеет вид
Найдем площадь фигуры интегрированиям:
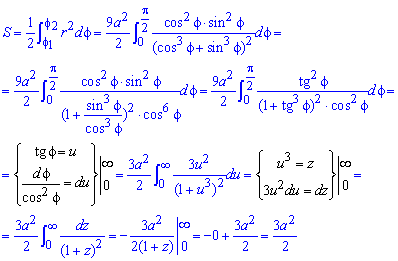
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
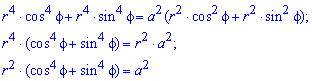
Выражаемый подинтегральную функцию делением:
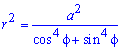
Запишем пределы интегрирования:
 (функция парная).
(функция парная).
Ее график изображен на рисунку
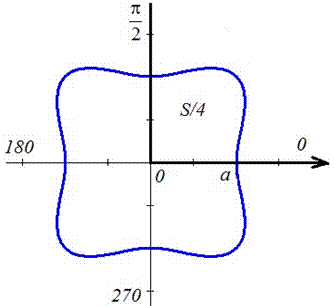
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
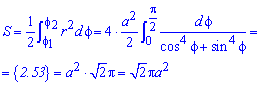
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
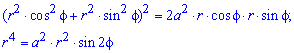
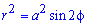 - подинтегральная функция.
- подинтегральная функция.
График исследуемой кривой следующий
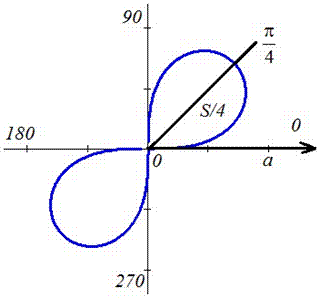
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 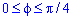 и результат умножим на 4 (смотри пример 2.106).
и результат умножим на 4 (смотри пример 2.106).
Находим площадь фигуры интегрированием:
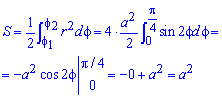
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.


