Невластивий інтеграл І роду
Якщо функція f(x) інтегровна за Ріманом на кожному кінцевому проміжку [a;b], тоді невластивий інтеграл знаходять через граничний перехід за формулою
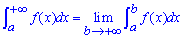
і говорять, що невластивий інтеграл збіжний, якщо існує така скінченна границя. В протилежному разі (якщо границя нескінченна або не існує) говорять, що інтеграл розбігається.
Невластивий інтеграл ІІ роду
Якщо функція f(x) необмежена в околі точки B і інтегровна за Ріманом на кожному кінцевому проміжку 
, тоді невластивий інтеграл ІІ роду обчислюють за формулою
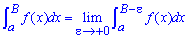
і говорять, що інтеграл збіжний, якщо існує його скінченна границя. В протилежному разі (якщо границя нескінченна або не існує) говорять, що інтеграл розбігається. Точка B називається особливою.
І. Обчислити інтеграли
Почнемо розгляд готових відповідей до невластивих інтегралів від простих до складних завдань.
Приклад 2.147 (2334) Знайти невластивий інтеграл
Маємо невластивий інтеграл І роду. Змінюємо безмежність на фіксовану точку з проміжку, обчислюємо інтеграл та після підстановки меж інтегрування знаходимо границю при прямуванні верхньої межі до безмежності
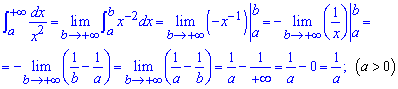
Приклад 2.148 ( 2335) Знайти інтеграл
Підінтегральна функція (логарифм) невизначена в нулі, що відповідає нижній границі інтегрування. Відповідно до наведених вище формул, маємо невластивий інтеграл другого роду. Для його знаходження переходимо до границі в нулі, також виконуємо інтегрування частинами
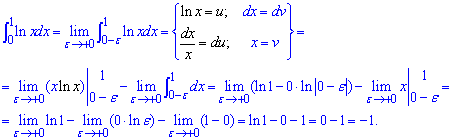
Сам по собі інтеграл не складний в плані обчислень.
Зауваження: надалі границю писати НЕ будемо, а при обчислення невластивих інтегралів розуміємо, що шукаємо значення границі в особливих точках (або в плюс мінус безмежності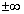 
)!!!
Приклад 2.149 (2336) Обчислити інтеграл
Розбиваємо інтеграл на 2 та знаходимо невластиві інтеграли І роду
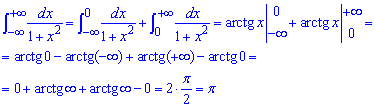
Приклад 2.150 (2337 ) Знайти інтеграл
Виконуємо маніпуляції ідентичні, як і в попередньому завданні та приходимо до невластивих інтегралів другого роду
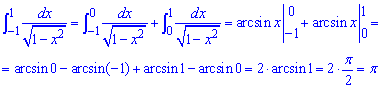
Приклад 2.151 ( 2338) Знайти інтеграл
Верхня границя прямує до безмежності, отже маємо невластивий інтеграл першого роду. Для знаходження граничного значення знаходимо неозначений інтеграл і при підстановці меж виносимо змінну за дужки в чисельнику і знаменнику логарифму. В результаті вклад нескінченно малих величин (1/x) прямує до нуля при змінній прямуючій до безмежності. Таким чином знаходимо головне значення інтегралу
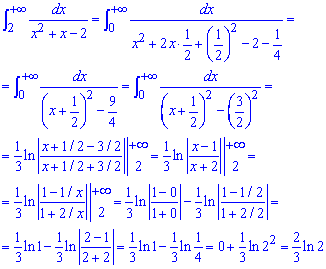
Приклад 2.152 (2339) Знайти інтеграл
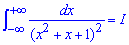
Розв'язання: Обчислимо останній інтеграл методом Остроградського - метод не з простих, проте ефективний в подібних обчисленнях:
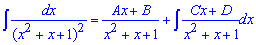
візьмемо похідну в кожній частині рівності (похідна від інтегралу рівна підінтегральній функції)
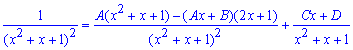
Зведемо дроби в правій частині рівності до спільного знаменника і прирівняємо коефіцієнти при відповідних степенях x кожної частини рівності
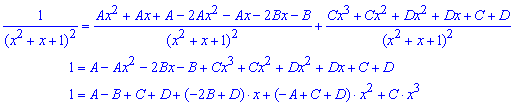
В результаті отримаємо систему із 4 лінійних рівнянь з якої знаходимо 4 константи
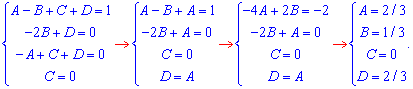
Таким чином можемо записати неозначений інтеграл у вигляді
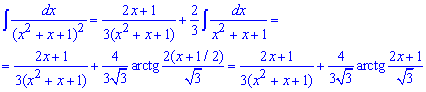
Далі підставляємо межі та знаходимо границі дробу та арктангенсу при змінній прямуючій до плюс міну безмежності.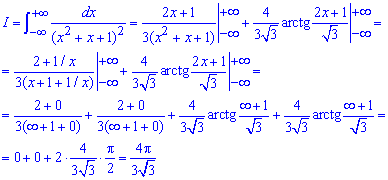 
В кінцевій формулі можна ще позбутися ірраціональності в знаменнику, але це вже старайтеся робити самостійно.
Приклад 2.153 ( 2340)Знайти інтеграл
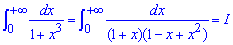
Обчислимо останній інтеграл методом невизначених коефіцієнтів:
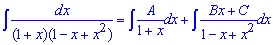
Записуємо підінтегральні функції та, звівши їх під спільний знаменник, а далі
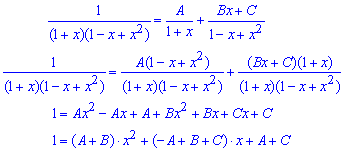
прирівняємо коефіцієнти при відповідних степенях x кожної частини рівності. В результаті розв'язуємо систему трьох рівнянь та визначаємо сталі
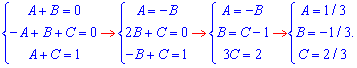
Підставимо їх в розклад та знайдемо неозначений інтеграл
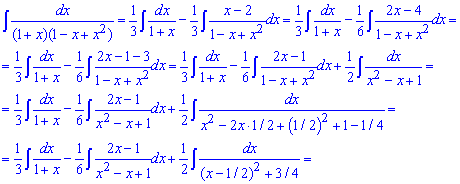
після зведення під табличні формули інтегрування отримаємо логарифми, які згрупуємо та арктангенс
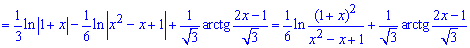
В безмежності виносимо з чисельника і знаменника дробу під логарифмом доданок із найстаршим показником і скорочуємо на нього. Тоді отримаємо логарифм одиниці.
В нулі з точністю до навпаки, сталі залишаємо - решта доданків із змінними не дають вкладу. З арктангенсом ситуація більш визначена і його значення на межі підставляємо у формулу
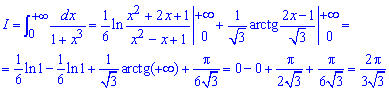
Приклад 2.154 ( 2341)Обчислити інтеграл
Покажемо, як можна знайти інтеграл такого вигляду двома способами.
І спосіб: розклад методом невизначених коефіцієнтів:
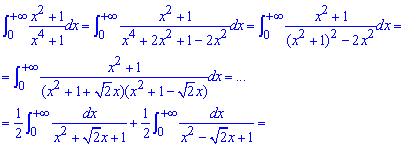
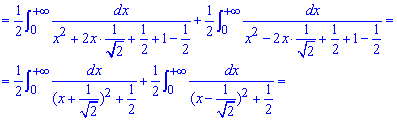
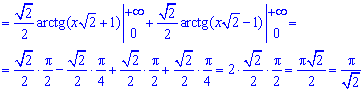
Чому рівний арктангенс в нулі, одиниці та безмежності Ви повинні знати на пам'ять при розв'язуванні подібних завдань.
Тут застосували метод невизначених коефіцієнтів (A=C=0; B=D=1/2):
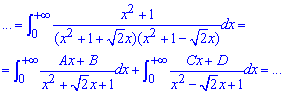
ІІ спосіб – через заміну змінних:
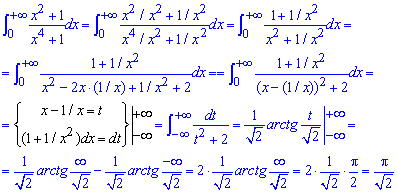
Межі інтегрування при заміні змінних тут стали іншими (в нулі мінус безмежність).
Приклад 2.155 (2342) Знайти інтеграл
Особливою точкою тут є нуль, оскільки корінь в знаменнику стає рівним нулю, а підінтегральна функція прямує до безмежності. Але це відбувається на такій малій ділянці інтегрування, що вклад мізерний і загалом інтеграл збіжний.
Для його обчислення переходимо під інтегралом до нових змінних, знаходимо нові межі інтегрування та знаходимо арктангенси на краях
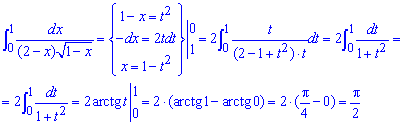
Обчислення не складні, оскільки використовуємо простий табличний інтеграл.
Приклад 2.156 (2343) Знайти інтеграл
В безмежності підінтегральна функція прямує до нуля, тому робимо висновок, що маємо невластивий інтеграл І роду. Для його знаходження дещо перетворюємо функцію та виконуємо заміну змінних
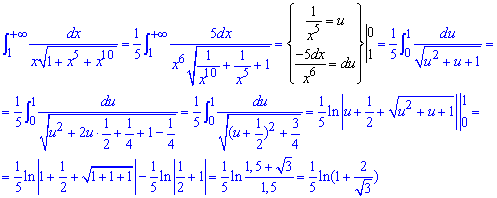
В результаті зводимо інтеграл до логарифма, який спрощуємо.
Приклад 2.157 ( 2344) Знайти інтеграл
Маємо невластивий інтеграл І роду. Виконуємо інтегрування частинами
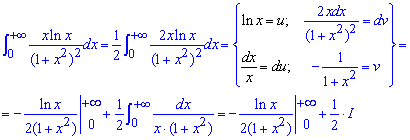
Другий доданок розкладаємо методом невизначених коефіцієнтів
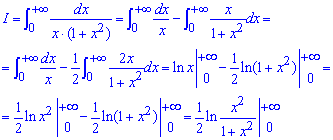
В результаті приходимо до випадку коли маємо невластивий інтеграл І та ІІ роду одночасно, тому тут границя матиме вигляд
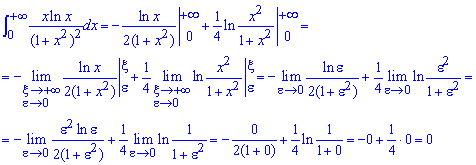
Тут враховано наступні граничні переходи
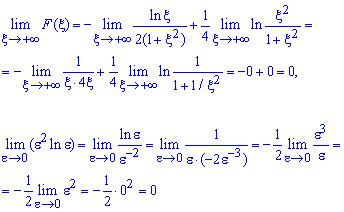
Отож інтеграл рівний нулю.
Приклад 2.158 (2345) Обчислити інтеграл
В безмежності підінтеграьна функція прямує до нуля - маємо І невластивий інтеграл.
Позначивши арктангенс через нову змінну визначаємо межі інтегрування, далі спрощуємо функцію та інтегруванням частинами знаходимо значення в крайніх точках.
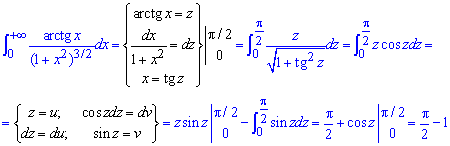
Приклад 2.159 (2346) Знайти інтеграл
Невизначений інтеграл І роду розриваємо двічі застосувавши інтегрування частинами
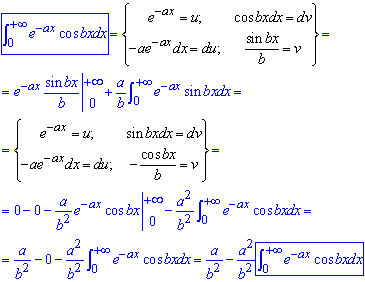
В результаті приходимо до запису інтегралу через самого себе, тобто рекурентної формули
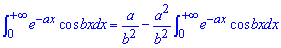
Перегруповуємо відомі та невідомі по різні сторони знаку рівності
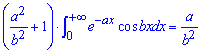
та виражаємо
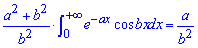; звідси
шуканий інтеграл
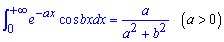
Метод не новий, та коли Ви маєте добуток експоненти на синуси та косинуси без нього не обійтися.
Приклад 2.160 ( 2347) Знайти інтеграл
В безмежності підінтегральний вираз дає нескінченно малу осцилюючу біля нуля функцію.
Щоб обійти таку невизначеність використовуємо методику попереднього прикладу. Двічі застосувавши інтегрування частинами
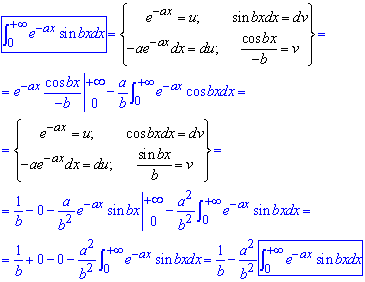
приходимо до рекурентної формули
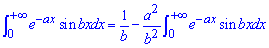
З неї знайти інтеграл досить просто: інтеграли переносимо в одну сторону, сталі в другу.
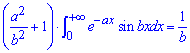
А далі виконуємо ділення одного сталої справа на множник при інтегралі
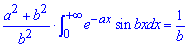
Звідси й маємо шуканий інтеграл
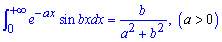
Запам'ятайте методику останніх двох завдань, на модулях та екзаменах на цьому поплатилася значна частина студентів.
Не попадіть до їх числа!
Приклад 2.161 Знайти інтеграл
Маємо невластивий інтеграл І роду. Знаходимо його та робимо висновок
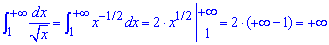
що інтеграл розбігається, оскільки границя не є скінченною.
Приклад 2.162 Знайти інтеграл
Експоненту інтегрувати не важко, при від'ємному показнику вона в безмежності прямує до нуля
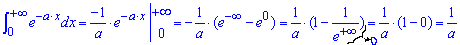
Приклад 2.163 Обчислити інтеграл
Інтеграл з виду не складний, однак при підстановці меж багато з Вас пишуть логарифм мінус логарифм = безмежність мінус безмежність, а далі що границя не існує, а інтеграл розбіжний. А він збіжний причому до нуля
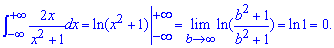
В цьому також легко переконатися проаналізувавши підінтегральну функцію, її знаменник додатний рівний для додатних і від'ємних значень змінної, чисельник непарна функція, отже інтеграл справа від осі абсцис нівелює інтеграл зліва.
Приклад 2.164 Знайти інтеграл
В знаменнику дробу виділяємо повний квадрат і зводимо інтеграл під формулу арктангенса.
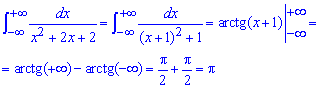
При прямуванні змінної до безмежності арктангенс прямує до Pi/2, при мінус безмежності до -Pi/2.
В сумі отримуємо Int=Pi.
Приклад 2.165 Знайти інтеграл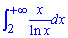 
Маємо інтеграл І роду. Покажемо, що він розбіжний. Знаменник на розглядуваному проміжку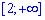 
задовільняє умову ln(x)<x-1 , тому маємо таку нерівність між функціями
,
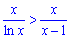Проте другий інтеграл розбіжний
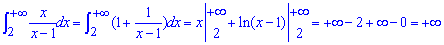
Оскільки функція приймає більші значення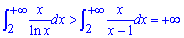 
, то заданий інтеграл 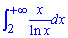також розбігається!
Приклад 2.166 Знайти інтеграл
Маємо невластивий інтеграл І роду. Його знаходимо розкладом підінтегральної функції через прості множники, як це реалізувати розписано далі
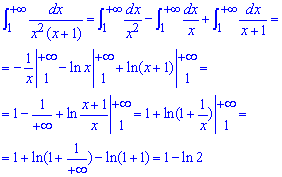
Даний інтеграл знайшли методом невизначених коефіцієнтів:
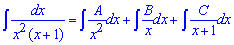
тобто записуємо функцію у вигляді розкладу простих дробів
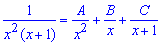
Далі їх зводимо до спільного знаменника
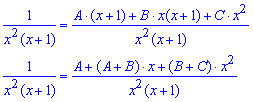
прирівняємо коефіцієнти при відповідних степенях x в обох частинах рівності і знаходимо сталі A=1, B=-1; C=1 . Їх і підставляємо в інтеграл
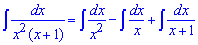
Приклад 2.167 Знайти інтеграл
Щоб не розкладати на прості роби через невизначені коефіцієнти додамо і віднімемо в чисельнику одиницю. Це дозволить отримати в чисельнику такий самий множник як вигляд знаменника і розкласти дріб на два інтеграли.
Подальше їх обчислення та визначення границь не важке і описується формулами
.
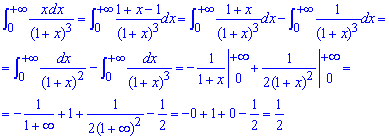Приклад 2.168 Знайти інтеграл
При змінній прямуючій до безмежності функція, що інтегрується прямує до нуля. Маємо невластивий інтеграл першого роду. Щоб знайти його значення виносимо змінну з під кореня знаменника , переходимо до нової змінної інтегрування (при цьому змінюються межі). В результаті отримаємо арксинус, який і обчислюємо
.
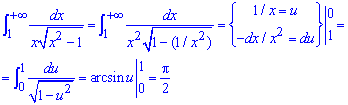Приклад 2.169 Знайти інтеграл
Тут необхідно, щоб параметр перетворювався в нуль. Для інших його значень невластивий інтеграл першого роду знаходимо методом заміни зміних. В результаті приходимо до логарифма, який розписуємо до найпростішого вигляду
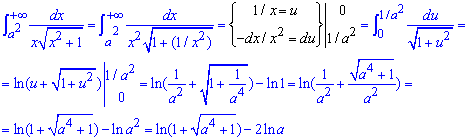
Приклад 2.170 Знайти інтеграл
Тут в нулі треба знайти границю, для цього обчислюємо невластивий інтеграл, та підставляємо межі.
Після цього отримаємо, що інтеграл рівний 0,5 .
Приклад 2.171 Знайти інтеграл
В нулі маємо особливість, яку при інтегруванні необхідно обійти. Спершу перетворюємо функцію, щоб перейти до нової змінної. Далі застосовуємо інтегрування частинами, якщо множником маємо експоненту то це швидко приводить до кінцевого результату або рекурентної формули. Далі підставляємо межі та аналізуємо, які доданки збігаються та до якої границі (значення).
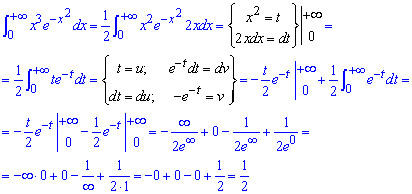
Приклад 2.172 Знайти інтеграл
В нескінченності синус осцилює, якщо помножити на змінну то отримаємо осцилюючу функцію зі зростаючою амплітудою. Виконуємо інтегрування частинами та переходимо до границі.
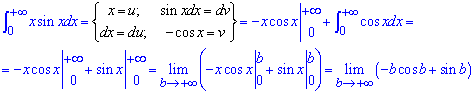
Оскільки остання границя не існує, то інтеграл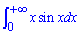 
розбіжний.
Приклад 2.173 Обчислити інтеграл
Оскільки ми знаємо до чого зводити подібні інтеграли, то виконуємо перетворення функції на початку. Ви ж можете позначити корінь з аргументу за нову змінну та в результаті перетворень прийти до того ж кінцевого інтегралу. Зінтегрувавши самостійно частинами, Ви отримаєте, що інтеграл рівний одиниці
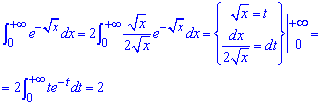
Приклад 2.174 Знайти інтеграл
В таких випадках потрібно двічі застосовувати інтегрування частинами.
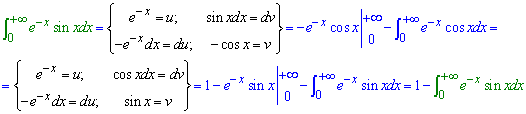
В результаті прийдемо до рекурентної формули
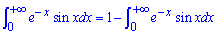
звідки і визначаємо інтеграл
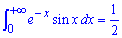
Даний інтеграл - це класика інтегрування, якщо б експонента та синус мали множники при аргументах, то обчислення були не такі прості.
Приклад 2.175 Знайти інтеграл
Тут з першого погляду може показатися, що інтеграл не належить до невластивих. Однак, розклавши знаменник на одночлени, бачимо, що у внутрішній точці має особливість, а саме розрив другого роду.
При знаходженні невластивого інтегралу другого роду при переході до границь два логарифми спрощуємо, за правилом різниця логарифмів рівна логарифму частки. Таким чином лише один з доданків дає вклад
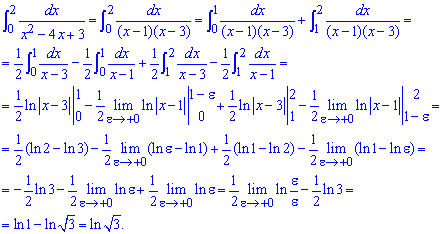
На графіку функції ця особливість має вигляд
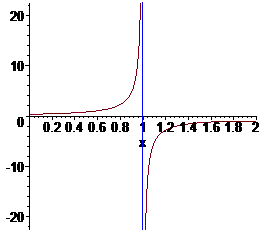
Приклад 2.176 Знайти інтеграл
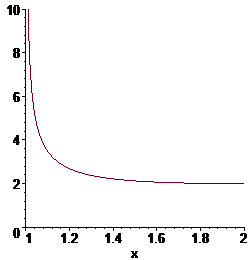
В одиниці корінь в знаменнику перетворюється в нуль і функція там має вертикальну асимптоту. Щоб її обійти додамо та віднімемо в чисельнику одиниці і розпишемо інтеграл на два. Їх обчислення вже не містить ніяких особливостей
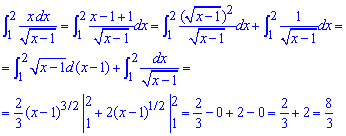
Графік функції не доходячи до 1 має вигляд
Приклад 2.177 Знайти інтеграл
Невизначеність в заданий інтеграл вносить те що логарифм в околі нуля прямує до мінус безмежності.
Зінтегрувавши частинами, прийдемо до особливості в нулі, Ви її можете звести до наслідку другої важливої границі, ми ж записуємо кінцеве значення.
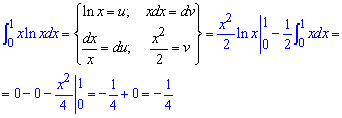
Для наочності графік підінтегральної функції на вказаному проміжку має вигляд
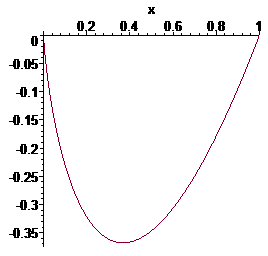
Як можна переконатися тут все гладко і красиво.
Приклад 2.178 Знайти інтеграл
При наближенні до нуля за рахунок квадрату знаменника функція зростає до безмежності. Але й при цьому проміжок на якому це відбувається прямує до нуля. Тому невластивий інтеграл існує і за допомогою наведеної заміни змінних знаходиться без проблем
.
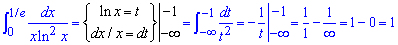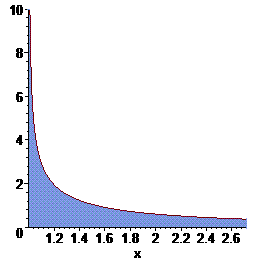
Знайдений інтеграл не що інше як площа фігури між функцією і віссю ординат. За виключенням особливості в нулі графік функції має вигляд верхньої лінії, а значення інтегралу - заштрихованій поверхні.
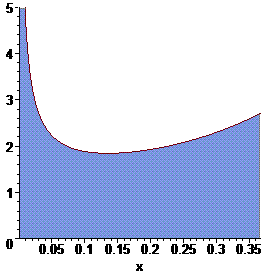
Приклад 2.179 Знайти інтеграл
В одиниці логарифм прямує до мінус безмежності, щоб його обійти виконуємо заміну змінних під інтегралом
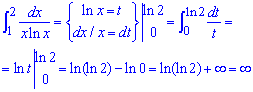
В результаті границя рівна безмежності, тому заданий інтеграл розбігається.
Графік підінтегральної функції в околі особливої точки має вигляд
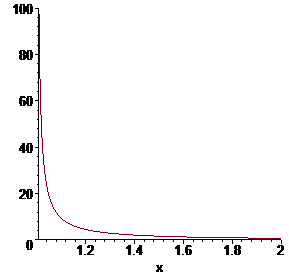
Приклад 2.180 Знайти інтеграл
При наближенні до одиниці логарифм прямує до нуля, а функція до плюс безмежності. Щоб обчислити невластивий інтеграл ІІ роду виконуємо заміну змінних і переходимо до кореневої функції в знаменнику, яка після інтегрування не має особливості
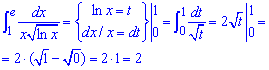
Значення інтегралу рівне площі заштрихованої фігури.
Приклад 2.181 Знайти інтеграл
Тут свій вклад вносить точка x=0, оскільки в ній функція з двох сторін прямує до плюс безмежності. Розділимо чисельник на знаменник та перепишемо функцію у вигляді показників змінної. Далі розділяємо інтеграл на два та знаходимо значення на межі.
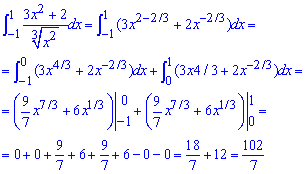
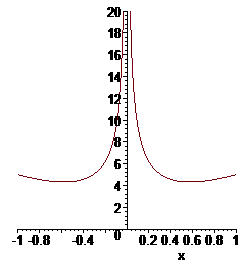
Отримали збіжний інтеграл. Вигляд функції наведено на рисунку
Приклад 2.182 Знайти інтеграл
Тут ідентична ситуація, в нулі має особливість. За схемою попереднього завдання знаходимо два невизначені інтеграли
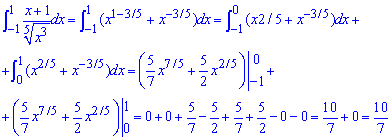
Приклад 2.183 Знайти інтеграл
Тут в нулі маємо особливість, але оскільки знаменник в нулі непарний то графік загальної функції має в нулі розрив другого роду. Такі функції інтегровні і за схемою вище знаходимо границю в нулі.
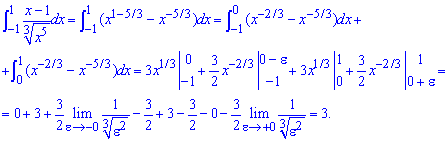
Біля 0 графік функції має вигляд
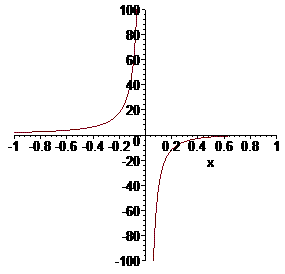
Приклад 2.184 (2348) Знайти інтеграл
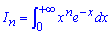
Обчислимо нульове наближення з усувною особливістю в нескінченності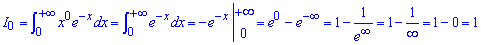
Далі інтегруванням частинами знаходимо значення для номера n
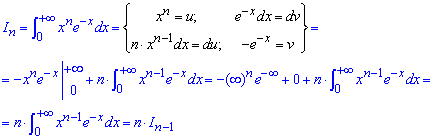
Отримали рекурентну формулу: In=n*In-1, звідси інтеграл рівний
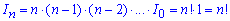
На цьому ознайомлення з основними прийомами знаходження невластивих інтегралів добігає кінця. Більше готових відповідей з інтегрування шукайте на сторінках сайту.
Потрібна допомога, також звертайтеся!
