Примеры на интегрирование с использованием правила замены переменных под интегралом изучают студенты 1, 2 курсов. Это в основном задачи для математиков, экономистов, статистов, физиков, химиков. Данные примеры задавали на контрольной работе в ЛНУ им. И. Франка. Чтобы формулы в задачах и ответах не повторялись сами задания выписывать не будем. Всем и так известно, что в задачах нужно или "Найти интеграл", или "Вычислить интеграл".
Пример 1. Нужно найти интеграл от дробной иррациональной функции. Для этого сначала корни превратим в показатели
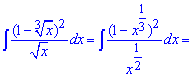
Далее в числителе возведем дужку к квадрату. Остается разделить числитель на знаменатель и по правилу суммы проинтегрировать каждое из слагаемых.
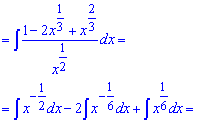
В результате интеграл примет значение
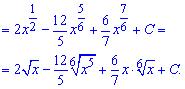
Пример 2. Вычисляем интеграл от произведения показательной функции на экспоненту. Для этого оба множителя вносим под общий степень и применяем формулуинтегрирования![]()
![]()
Пример 3. Для нахождения интеграла под корнем выполним преобразования, которые позволят получить при переменной коэффициент единицу. Это удобно для прямого применения табличной формулы
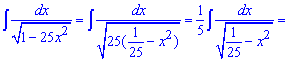
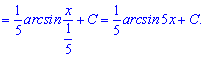
Поскольку имеем дело с неопределенными интегралами то следует не забывать добавить в конце постоянную.
Замена переменных под интегралом
Пример 4. Для вычисления интеграла обозначим дужку в знаменателе за новую переменную. Далее найдем dx и подставим в интеграл
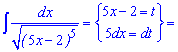
![]()
В конце не забываем вернуться к замене, которую делали в начале.
![]()
Пример 5. Для вычисления интеграла от дроби тригонометрических функций следует выполнить следующую замену. Ее трудно заметить, однако производная от котангенса равна минус единицы разделенной на синус в квадрате, то есть знаменателе дроби. Таким образом интеграл преобразуем к следующему
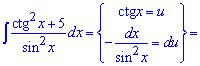
![]()
После интегрирования подставляем сделанную замену.
![]()
Пример 6. Нужно найти интеграл от экспоненты умноженной на иррациональную функцию от экспоненты. Для упрощения возьмем выражение под корнем за новую переменную и найдем остальные необходимых для интегрирования величины.
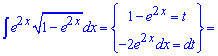
После интегрирования возвращаемся к замене.
![]()
Пример 7. На вид сложный интеграл имеет простое решение. Все что для Вас создает трудности при интегрировании отмечайте за новую переменную. В этом задании особенность вносит функция под синусом. Ее и обозначим за u, и найдем дифференциал du
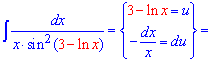
Интеграл упростится до табличного значения, после его нахождения выполняем замену переменных.
![]()
Как только Вы изучите приведенные схемы интегрирование и сможете самостоятельно найти подобные интегралы - тогда контрольная работа не будет для Вас чем то сложным в обучении. Если в обучении встречаются сложные интегралы, которые Вы не в силах решить, помните - мы всегда готовы оказать помощь. Это предложение актуально как для студентов стационарной формы обучения, так и для заочников и школьников. Те кто заочно учатся получают очень слабую теоретическую базу для понимания всей силы формул интегрирования.
Готовые решения контрольной по интегрированию


