Контрольну роботу на інтегрування функцій подібного складу завдань задають студентам 1, 2 курсів. Це здебільшого завдання для математиків, економістів, статистів, прикладників. Дані приклади задавали на контрольній роботі в ЛНУ ім. І. Франка, "Львівська Політехніка", КНЕУ також практикує подібні контрольні з інтегрування. Щоб формули в завданнях і відповідях не повторювалися самі завдання описувати не будемо. Всім і так відомо, що в завданнях потрібно або "Знайти інтеграл" , або "Обчислити інтеграл".
Приклад 15. Ми дійшли до інтегрування дробово раціональних функцій. Вони займають особливе місце серед інтегралів, оскільки вимагають багато часу на обчислення та допомагають викладачам перевірити Ваші знання не тільки з інтегрування. Для спрощення функції під інтегралом додамо та віднімемо вираз, який дозволить розбити функцію під інтегралом на два доданки
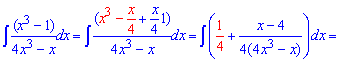
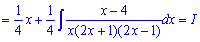
В результаті один інтеграл знаходимо доволі швидко, в іншому потрібно дріб розкласти на прості доданки
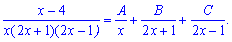
При зведенні до спільного знаменника отримаємо такі чисельники
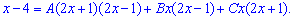
розкриваємо дужки і спрощуємо
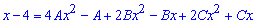
Прирівнюємо значення при однакових степенях "ікс" справа та зліва. В результаті прийдемо до системи трьох лінійних рівнянь (СЛАР) з трьома невідомими.
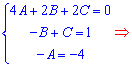
Як розв'язувати системи рівнянь описано в інших статтях сайту. В кінцевому варіанті Ви отримаєте такі розв'язки СЛАР
A=4; B=-9/2; C=-7/2.
Підставляємо сталі в розклад та виконуємо інтегрування
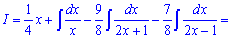
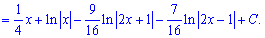
На цьому приклад розв'язано.
Приклад 16. Знову потрібно знайти інтеграл від дробово раціональної функції. Для початку кубічне рівняння, що міститься в знаменнику дробу розкладемо на прості множники
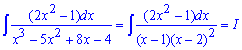
Далі розкладаємо дріб на прості множники
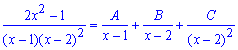
Зводимо праву сторону до спільного знаменника та розкриваємо дужки в чисельнику.
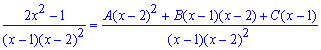
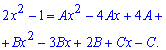
Прирівнюємо коефіцієнти при однакових степенях змінної. В результаті отримаємо СЛАР з трьома невідомими
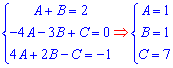
Підставляємо сталі в розклад та обчислюємо інтеграл
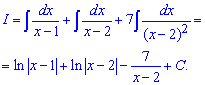
Перші два доданки дають логарифм, останній теж легко знайти.
Приклад 17. В знаменнику дробово раціональної функції маємо різницю кубів. Її за формулами скороченого множення розкладаємо на два множники
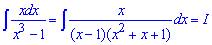
Далі отриману дробову функцію розписуємо на прості доданки та зводимо їх під спільний знаменник
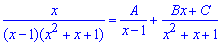
В чисельнику отримаємо наступний вираз.
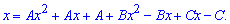
З нього формуємо систему лінійних рівнянь для обчислення 3 невідомих
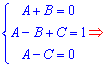
A=1/3; B=-1/3; C=1/3.
Підставляємо сталі у розклад та інтегруємо кожен із доданків. В результаті інтеграл прийме значення
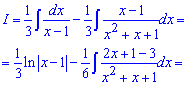
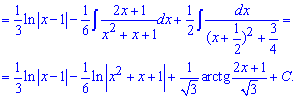
Тут чисельник другого інтегралу перетворювали під логарифм. Залишок при інтегруванні дає арктангенс.
Як тільки Ви вивчите наведені схеми та методики зведення інтегралів під те чи інше правило, навчитеся бачити в прикладах табличні інтеграли та перетворення, які в кілька кроків дозволять Вам знайти інтеграл – то будь-яка контрольна робота, чи "зрізи" для Вас не будуть перешкодою в навчанні. Для цього потрібно розв'язати з десяток різних інтегралів до кожного з наведених прикладів. Всі решта після цього будуть для Вас подібними, а схема їх обчислень очевидною і зрозумілою для Вас. Якщо в навчанні зустрічаються складні інтеграли, або ж маєте сумніви у власних силах пам'ятайте – ми завжди готові надати допомогу. Як на контрольних так і на тестах, ця пропозиція актуальна не тільки для студентів стаціонарної форми навчання, а й для заочників та школярів. В 11 класі в навчанні з недавніх часів школярам також доводиться мати справу з інтегралами.
Готові розв'язки контрольної з інтегрування


