Інтегрування раціональних дробів. Методика

Інтегрування раціональних дробів займає важливу частину курсу вищої математики. Практична сторона даної теми багата на різноманітні обчислення. Нагадаємо, що дріб

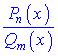
називається раціональним, якщо чисельник P_n(x) та знаменник Q_m(x) є многочлени.
Раціональні дроби поділяють на правильні та неправильні. Дріб називається правильним, якщо найвищий показник степеня чисельника n менший від найвищого степеня знаменника m. У іншому випадку дріб називається неправильним. Інтегруються лише правильні дроби. Неправильний раціональний дріб у якого степінь чисельника вищий або дорівнює степені знаменника можна діленням чисельника на знаменник звести до cуми многочлена та правильного раціонального дробу.

Типи раціональних дробів

Найпростішими раціональними дробами називають наступні

І.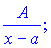

ІІ.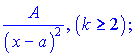

ІІІ.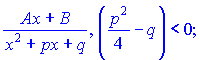

ІV.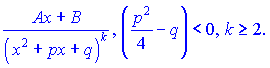

Умова 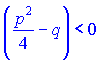означає, що квадратне рівняння x²+px+q не має дійсних коренів. В іншому випадку його можна розкласти на множники і звести до 1 типу.
Для всіх чотирьох груп існують правила зведення до табличного вигляду і інтегрування. Інтеграли І та ІІ типу знаходять методом безпосереднього інтегрування

І.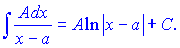

ІІ.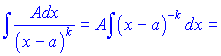

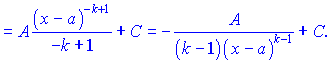
При інтегруванні найпростішого дробу ІІІ-го типу потрібно виконати наступні перетворення.



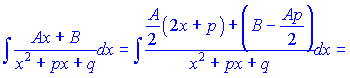
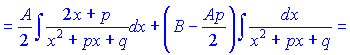
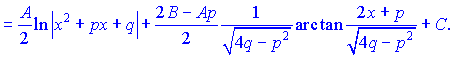
Інтеграл від найпростішого дробу IV-го типу шляхом повторного інтегрування частинами можна звести до інтегралу від найпростішого дробу III-го типу. Інтеграл від дробово-раціональної функції 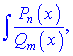де 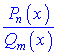– правильний дріб, можна звести методом розкладу на доданки, які легко інтегруються за основними формулами інтегрування. Усі правильні раціональні дроби розкладаються на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів. Кінцевий вигляд найпростіших дробів залежить від коренів знаменника Q_m(x) та їх кратності.

Можливі наступні варіанти поліномів:

1. Корені знаменника – дійсні та різні числа, тобто
Q_m(x)=(x-a)(x-b)...(x-d)
Тоді дріб розкладається на суму найпростіших дробів І-го типу

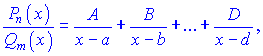
де A, B, ..., D – невідомі коефіцієнти. Їх знаходять наступним чином: доданки справа зводять до спільного знаменника, а потім прирівнюють отримані коефіцієнти при степенях x чисельника з тими, які містить поліном P_n(x).

2. Корені знаменника дійсні числа, деякі з них кратні k
Q_m(x)=(x-a)...(x-b)^k.
В цьому випадку правильний дріб розкладається на суму найпростіших дробів І-го та ІІ-го типів:

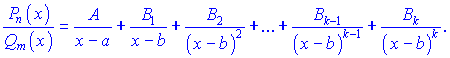
Невідомі коефіцієнти A, B₁, B₂,..., B_k шукаємо методом невизначених оефіцієнтів.

3. Деякі корені знаменника дійсні числа, деякі з них кратні. Крім того знаменник містить один або декілька квадратних тричленів, які не розкладаються на множники
Q_m(x)=(x-a)...(x-b)^k...(x²+px+q).
Тоді дріб розкладається на суму найпростіших дробів І-го, ІІ-го та ІІІ-го типів

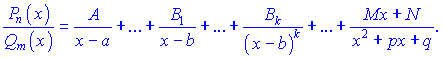
Тут A, B₁, B₂,..., B_k, M, N – невідомі коефіцієнти, які шукають за схемою поданою вище (неозначені коефіцієнти).

4. Цей випадок відрізняється від попереднього тим, що в знаменнику дробів квадратні тричлени бувають в степенях >=2. В таких випадках можемо отримати суму найпростіших дробів І-ІV-го типів. Вони найскладніші, але наведеними вище методами їх розв'язування можливе.
Практична сторона інтегрування раціональних дробів детально розглянута в наступній статті.