Контрольну роботу на інтегрування функцій подібного складу завдань задають студентам 1, 2 курсів. Це здебільшого завдання для математиків, економістів, статистів, програмістів. Дані приклади задавали на контрольній роботі в ЛНУ ім. І. Франка, "Львівська Політехніка", КНЕУ також практикує подібні контрольні з інтегрування. Щоб формули в завданнях і відповідях не повторювалися самі завдання описувати не будемо. Всім і так відомо, що в завданнях потрібно або "Знайти інтеграл" , або "Обчислити інтеграл".
Приклад 18. Для розкриття ірраціональності в знаменнику дробу необхідно в подібних прикладах виконувати таку заміну змінних – змінну в найменшому степені. В результаті прийдемо до інтегралу від дробової функції
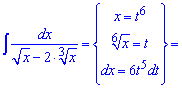
далі виконуємо ділення чисельника на знаменник та спрощення
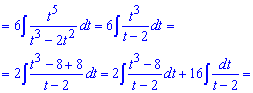
Таким чином без громіздких розписувань дробів перейдемо до інтегралу
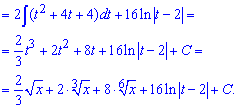
Приклад 19. Підкореневу функцію позначаємо за нову змінну в квадраті (для зручності обчислень). Далі знаходимо диференціал змінної, підставляємо в неозначений інтеграл та виконуємо спрощення.
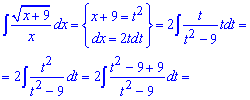
В результаті заміни отримаємо дріб, який розщеплюється на два інтеграли. Другий інтеграл рівний частці логарифмів
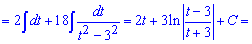
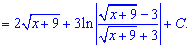
Приклад 20. Наступні інтеграли стосуються виключно тригонометричних функцій, а саме їх добутку, квадратів, кубів, раціональних функцій. Перший з наведених інтегралів потрібно звести виключно до синуса. Для цього косинус в 5 степені розписуємо на добуток косинуса в 4 степені на косинус, який вносимо під диференціал


Для спрощення вводимо заміну змінних та приходимо до інтегрування поліному
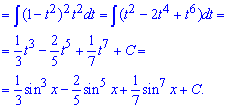
Вкінці інтегрування повертаємося до заміни, і замість t усюди записуємо sin(x).
Приклад 21. Для обчислення інтегралу потрібно понизити степінь синуса. Таким чином використовуємо тригонометричні формули, понижуємо степінь до першого, а далі знаходимо інтеграл за табличними формулами.
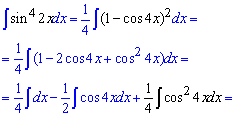
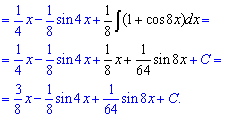
Приклад 22. Потрібно знайти інтеграл від добутку подвійного синуса на потрійний косинус. Під диференціал нічого внести не вдасться, оскільки маємо різні інтеграли. Для спрощення розпишемо добуток тригонометричних функцій через різницю синусів
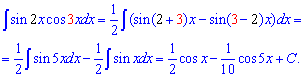
Приклад 23. Даний інтеграл без універсальної тригонометричної заміни змінних знайти не вдасться. Тому тангенс половини кута нехай рівний t, тоді синус перетвориться за формулою
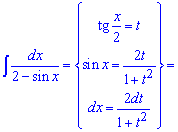
Після розкриття дужок в знаменнику отримаємо квадратний тричлен
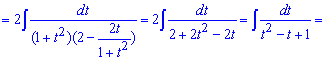
Для зведення такого дробу під табличний арктангенс в знаменнику спершу виділяємо квадратний тричлен
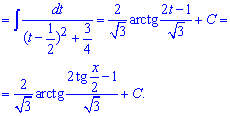
Не забуваємо наприкінці повернутися до виконаної на початку заміни. Це важливо при тестах та контрольних.
Приклад 24. Тут можемо використати універсальну тригонометричну заміну, а може піти іншим шляхом. Винесемо в знаменнику синус в квадраті за дужки та перегрупуємо доданки в дужках, щоб за тригонометричними формулами отримати котангенс. Його і позначимо за нову змінну u, обчислюємо також диференціал du та підставляємо все у інтеграл )
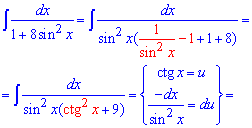
В результаті інтегрування отримаємо табличну формулу арктангенса
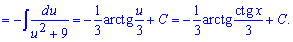
Приклад 25. Необхідно обчислити інтеграл від тангенса в квадраті від потрійного аргументу. Спершу розписуємо тангенс, як частку синуса до косинуса. Далі синус в квадраті розписуємо через косинус. Після ділення чисельника на знаменник отримаємо два інтеграли, які без труднощів знаходимо за формулами інтегрування
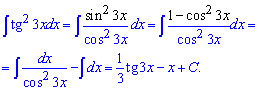
Як тільки Ви вивчите наведені схеми та методики зведення інтегралів під те чи інше правило, навчитеся бачити в прикладах табличні інтеграли та перетворення, які в кілька кроків дозволять Вам знайти інтеграл – то будь-яка контрольна робота, чи "зрізи" для Вас не будуть перешкодою в навчанні. Для цього потрібно розв'язати з десяток різних інтегралів до кожного з наведених прикладів. Всі решта після цього будуть для Вас подібними, а схема їх обчислень очевидною і зрозумілою для Вас. Якщо в навчанні зустрічаються складні інтеграли, або ж маєте сумніви у власних силах пам'ятайте – ми завжди готові надати допомогу. Як на контрольних так і на тестах, ця пропозиція актуальна не тільки для студентів стаціонарної форми навчання, а й для заочників та школярів. В 11 класі в навчанні з недавніх часів школярам також доводиться мати справу з інтегралами.
Готові розв'язки контрольної з інтегрування


