Зміна меж при зміні порядку інтегрування

Продовжуємо розбирати готові приклади на зміну порядку інтегрування в подвійному інтегралі. Як визначати точки перетину кривих, шукати обернені функції та розбивати область інтегрування на підобласті Вам вже має бути відомо з попереднього уроку. Перегляньте уважно наведені завдання і добре розберіть як змінюємо межі при зміні порядку інтегрування.

ЗАВДАННЯ 3.5 В подвійному інтегралі змінити порядок інтегрування:

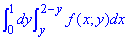
Розв'язання: Побудуємо область інтегрування, що обмежена заданими прямими
0≤y≤1, y≤x≤2-y, тут x=y і x=2-y - прямі.
Побудуємо підінтегральну область та заштрихуємо, які нам потрібні при обчисленнях

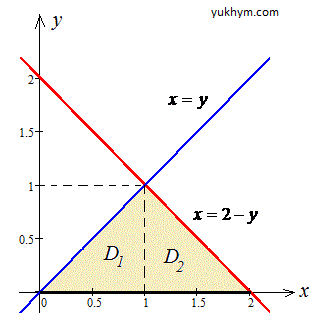
Бачимо, що при зміні порядку інтегрування область інтегрування необхідно розділити на дві підобласті D=D₁+D₂
D₁: 0≤x≤1, 0≤y≤x;
D₂: 1≤x≤2, 0≤y≤2-x.
Це зумовлено тим, що нижня межа по ігрику в нас постійна, а верхня змінюється при проходженні "іксів" від 0 до 2.
При цьому подвійний інтеграл можемо замінити сумою двох

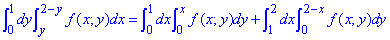
Результат при цьому залишиться однаковим.

ЗАВДАННЯ 3.6 Змінити порядок інтегрування:

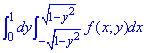
Розв'язання: Побудуємо область інтегрування, що обмежена кривими
0≤y≤1,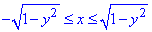
Межі за змінною "ікс" описують x=√(1-y²), x²=1-y², x²+y²=1² - праве півколо з центром у точці O(0;0) і радіусом 1;
x=-√(1-y²) - ліве півколо з тими ж характеристиками.
Графік області інтегрування наведено нижче

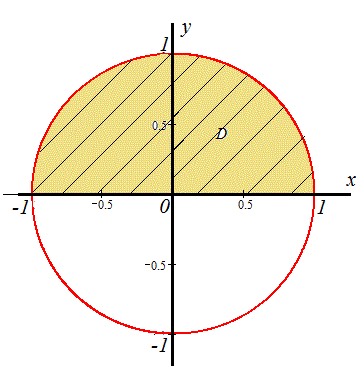
Виразимо отримані функції через змінну y:
x²+y²=1² , y=√(1-x²) - верхнє півколо, бо 0≤y≤1.
Межі інтегралів приймуть значення:
-1≤x≤1, 0≤y≤√(1-x²).
Записуємо як поміняється подвійний інтеграл при зміні порядку інтегрування

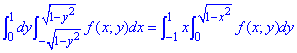
ЗАВДАННЯ 3.7 Змінити порядок інтегрування:

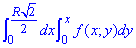
Розв'язання: Область інтегрування в даному прикладі обмежена двома прямими
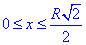, 0≤y≤x, де y=x - пряма.
Дехто міг подумати, що десь має бути коло, оскільки верхня межа по "ікс" містить R.
Побудуємо область інтегрування

 
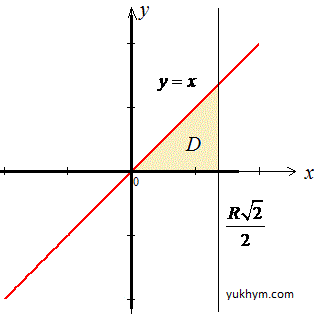
Розставляємо межі при зміні порядку інтегрування
D: 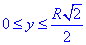, 0≤x≤y.
Подвійний інтеграл перетвориться наступним чином:

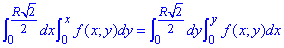
ЗАВДАННЯ 3.8 Змінити порядок інтегрування:

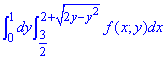
Розв'язання: Розпишемо область інтегрування, що обмежена кривими
0≤y≤1,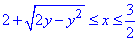
Приведемо до канонічного вигляду запис
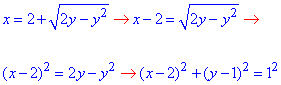- праве півколо з центром у точці O(2;1) і радіусом R=1.
Підінтегральна область матиме наступний вигляд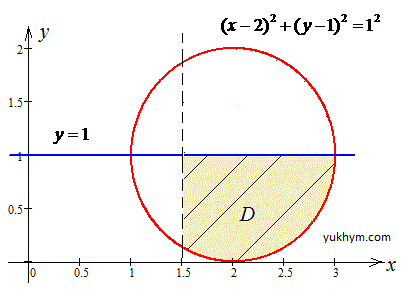
 
Виразимо отримані функції через змінну x:
(x-2)²+(y-1)²=1, звідси 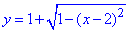(тут y>0);
Проведемо розстановку меж інтегрування в заданій області D:
1,5≤x≤3,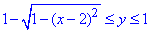
Можемо записати інтеграл зі зміненим порядком інтегрування

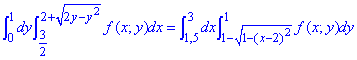
ЗАВДАННЯ 3.9 Змінити порядок інтегрування:

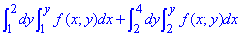
Розв'язання: Бачимо, що в умові задано суму двох інтегралів.
Отже на площині область інтегрування складається з двох областей
D₁: 1≤y≤2, 1≤x≤y,
D₂: 2≤y≤4, 2≤x≤y,
де y=x - пряма.
Графічно ці області представимо рисунком

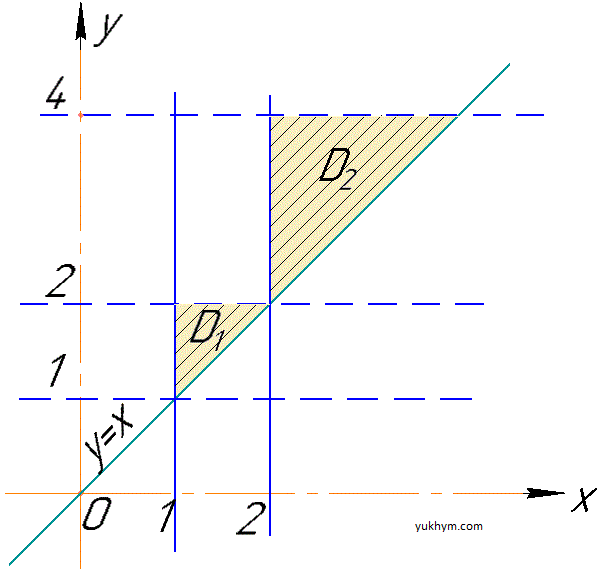
Не лякайтеся подібних завдань, області які обмежені прямими найлегше інтегрувати.
Розставимо межі в областях D₁, D₂:
D₁: 1≤x≤2 , x≤y≤2;
D₂: 2≤x≤4, x≤y≤4.
Уважно перегляньте чому саме так змінюються межі інтегрування.
Виконуємо зміну порядку інтегрування

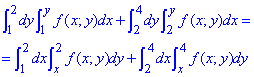
Ось так просто можна обчислювати, якщо добре знати теорію та вміти інтегрувати на практиці.
Учіться і бажаємо Вам так же легко обчислювати на практиці!