Змінити порядок інтегрування в подвійному інтегралі

Сьогодні детально проаналізуємо алгоритм зміни порядку інтегрування в подвійному інтегралі. Під зміною порядку інтегрування маємо на увазі, що задано подвійний інтеграл в якому інтегрування проводиться спершу по "ікс", а далі отриманий результат інтегрують по "ігрик". Потрібно поміняти межі інтегрування, а можливо й розбити на декілька областей інтегрування, для того, щоб спершу інтегрувати по "ігрику", а далі по "іксу". В курсі вищої математики подібні приклади вчать вирішувати досить тривалий час, але не у всіх це виходить. Схема зміни порядку інтегрування буде розписана на готових прикладах з гарно виконаними рисунками областей інтегрування. Хтось може подумати, що рисунки тут ні до чого, але прочитавши статтю до кінця Ви зрозумієте, що без рисунків Ви не зможете зрозуміти як змінюються межі, та як їх правильно розставляти.

ЗАВДАННЯ 3.1 Змінити порядок інтегрування в подвійному інтегралі:

Розв'язання: Побудуємо область інтегрування, яка обмежена кривими
0≤x≤4, 3x²≤y≤12x, де
y=3x² - парабола з вершиною у точці O(0;0) і гілками вгору;
y=12x - пряма, що проходить через точку O(0;0).
Графік області інтегрування наведено далі.

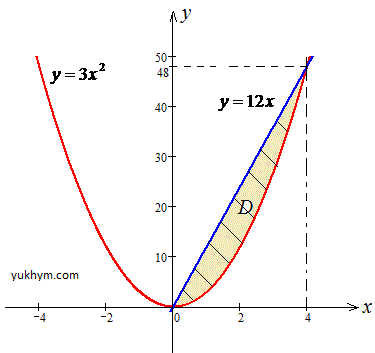
В цьому прикладі "ігрик" змінюється від нижньої кривої (параболи) до верхньої (прямої), в цей час "ікс" пробігає значення від 0 до 4.
При зміні порядку інтегрування ми будемо пробігати значення від першої кривої по "іксу" (прямої) до другої (параболи), "ігрик" в цей час буде проходити значення від 0 до другої точки перетину заданих кривих.
Звідси слідує, що для зміни порядку інтегрування потрібно знайти точки перетину кривих, далі для зміни меж потрібно перейти від y(x) до x(y) для цих самих меж.
Виразимо задані функції y(x) через змінну y:
y=3x², звідси 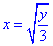(перед коренем взяли знак "+", оскільки x≥0),
y=12x, звідси x=y/12.
Їх точки перетину: y=3x²=12x, звідси

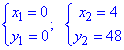
Розставимо межі в заданій області:
D: 0≤y≤48,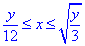

Виконуємо зміну порядку інтегрування в інтегралі

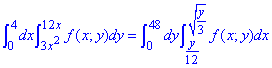
Ось і вся схема переходу від інтегрування по y,x до подвійного інтеграла по x,y.

ЗАВДАННЯ 3.2 Змінити порядок інтегрування:

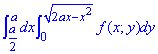
Розв'язання: Запишемо область інтегрування для заданого прикладу
a/2≤x≤a, 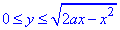, де y=0 - вісь абсцис.
Перетворимо верхню криву по y до канонічного вигляду
y=√(2ax-x²), y²=2ax-x², x²-2ax+a²+y²=a², (x-a)²+y²=a² - верхнє півколо з центром у точці O(a;0) і радіусом a.
На рисунку наведемо область інтегрування

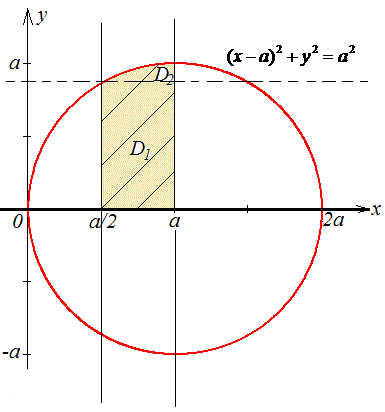
Знайдемо запис функції через змінну y:
(x-a)2+y2=a2, (x-a)2 =a2-y2,

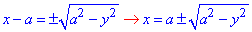
При зміні порядку інтегрування нашу область необхідно розбити на дві підобласті:
D=D₁+D₂.
Розставимо межі в кожній області:
D1: 0≤y≤a√3/2, a/2≤x≤a;
D2: a√3/2≤y≤a,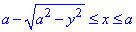
Далі можемо змінити порядок інтегрування

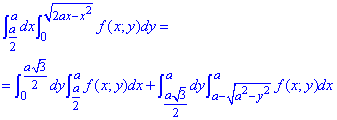
Уважно перегляньте фрагмент де область інтегрування розбивається на 2, чому це робиться та від чого залежить.
Багато хто цього не розуміє, оскільки не уявляє що робимо, тут же маємо графік з якого бачимо, що в першій області "ікс" змінюється від першоїї прямої x=a/2до другої x=a, в другій області змінна "ікс" пробігає значення від півкола до прямої x=a.

ЗАВДАННЯ 3.3 Змінити порядок інтегрування:

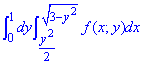
Розв'язання: Область інтегрування обмежена кривими
0≤y≤1, 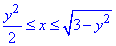, де x=y²/2 - парабола з вершиною в точці O(0;0) і гілками вправо,
x=√(3-y²), x²=3-y², x²+y²=(√3)² - праве півколо з центром у точці O(0;0) і радіусом R=√3.
Для зміни порядку інтегрування виразимо отримані функції через змінну x:
x=y²/2, y²=2x, y=√(2x); x²=3-y², y²=3-x², y=√(3-x²).
Знайдемо точки перетину графіків функцій:
параболи з горизонтальною прямою

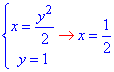
параболи з правою частиною півкола (І чверть)

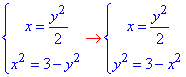
Підставляємо y² з другого рівняння системи рівнянь в перше x=1,5-0,5x²;
При розв'язуванні отримаємо x=1.
Виконуємо побудову та розбиття на потрібні підобласті інтегрування

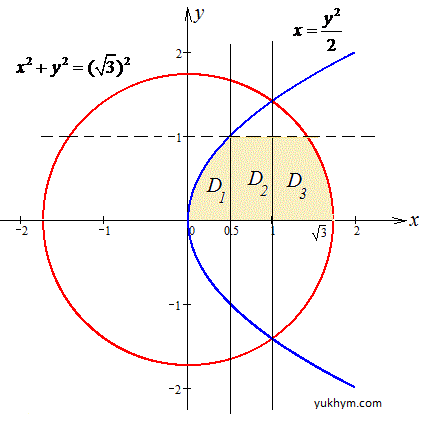
Для зміни порядку інтегрування нашу область розіб'ємо на три підобласті:
D=D₁+D₂+D₃.
Розставимо межі в кожній області:
D1: 0≤x≤0,5, 0≤y≤√(2x);
D2: 0,5≤x≤1, 0≤y≤1;
D3: 1≤x≤√3, 0≤y≤√(3-x²).

Уважно розберіться, як це зіставити з областями на рисунку та чому саме таке розбиття тут потрібно виконувати.
Запишемо як зміниться інтеграл при зміні порядку інтегрування

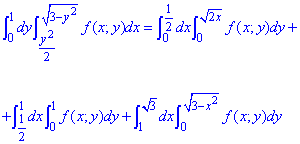
Думаю наведених пояснень достатньо, щоб самостійно навчитися міняти порядок інтегрування.

ЗАВДАННЯ 3.4 Змінити порядок інтегрування:

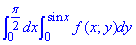
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими
0≤x≤π/2, 0≤y≤sin(x), де y=0 - вісь абсцис;
y=sin(x) - синусоїда.
Виразимо отримані функції через змінну y:
y=sin(x), звідси x=arcsin(y);
y=0, звідси x=0.
Графіки кривих наведемо на рисунку

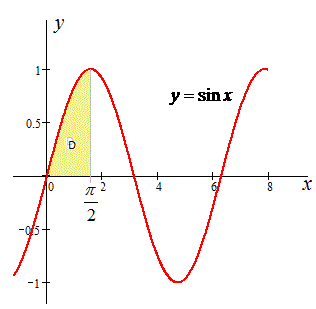
Межі інтегрування в заданій області поміняються на такі:
D: 0≤y≤1, 0≤x≤ arcsin(y).
Записуємо подвійний інтеграл з перерахованими межами інтегрування

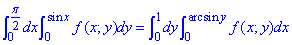
Маємо ще 5 готових прикладів на зміну порядку інтегрування, їх Ви можете переглянути в наступній статті.