Приклади на інтегрування функцій взято з матеріалів контрольної роботи, яку задають студентам 1, 2 курсів математичних факультетів. Для економії Вашого часу самі умови завдань пропущені, всюди потрібно або "Знайти неозначений інтеграл" або "Обчислити інтеграл". Тексту в коментарях до кожного завдання рівно стільки, скільки потрібно Вам для засвоєння матеріалу і вивчення методики та схем інтегрування.
Інтегрування тригонометричних функцій
Приклад 20. Для обчислення інтегралу від добутку косинуса та синуса необхідно синус внести під диференціал. В результаті перейдемо до інтегрування показникової функції від косинуса. Через формули це матиме наступний запис
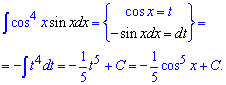
Приклад 21. Спершу слід проаналізувати аргументи під синусом та косинусом та показники. Добуток функцій можемо записати через квадрат синуса подвійного кута, який в свою чергу записуємо через косинус в два рази більшого аргументу. Як тільки дійдемо до функцій в першому степені маємо право застосовувати табличні інтеграли
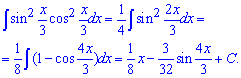
Приклад 22. Косинус подвійного кута записуємо згідно тригонометричних формул через косинус 1 кута. Далі, щоб отримати інтеграл від однієї з тригонометричних функцій необхідно синус внести під диференціал. Подальші обчислення зводяться до інтегрування простих функцій
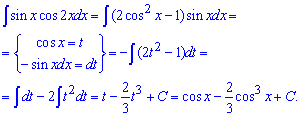
Слід зазначити, що в цьому та попередньому прикладі використовували деякі тригонометричні формули. Для обчислення всіх можливих інтегралів, але для розв'язання базових інтегралів необхідно не більше 10 популярних тригонометричних формул.
Приклад 23. Маємо дробову тригонометричну функцію. Для її обчислення необхідно застосувати універсальну тригонометричну заміну – тангенс половини кута. Синус через тангенс половини кута виражається залежністю 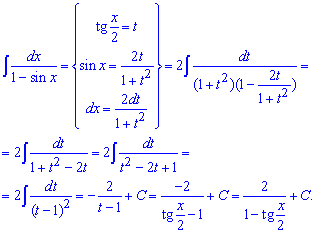
Після підстановки заміни в інтеграл та спрощення, що при таких замінах буває не простим, отримаємо просту дробову функцію. Її інтегрувати повинен вміти кожен студент. Якщо ні, то контрольна чи самостійна на інтеграли покаже "хто є хто".
Приклад 24. Щоб знайти інтеграл можна застосувати універсальну тригонометричну заміну, як один із поширених способів. Як альтернативний варіант можна винести квадрат косинуса за дужки, а в дужках додати та відняти одиницю, щоб отримати тангенс. Далі його позначаємо за нову змінну та обчислюємо диференціал (він співпаде з другою частиною підінтегральної функції). Таким способом перейдемо до інтегрування функції, яка зводиться до арктангенса.
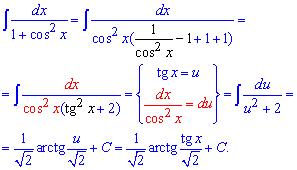
Такий підхід дещо спрощує обчислення, але не завжди легко його побачити та застосувати.
Приклад 25. Інтеграл від котангенса в квадраті від потрійного аргументу знаходимо після наведених нижче перетворень
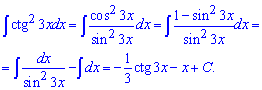
Тут використана проста залежність, що сума квадратів синуса та косинуса рівна одиниці.
Приклад 1*. Обчислити невизначені інтеграли від тригонометричних функцій.
а) Уважно проаналізуйте методику інтегрування частинами такого типу прикладів, та як до цього прийти
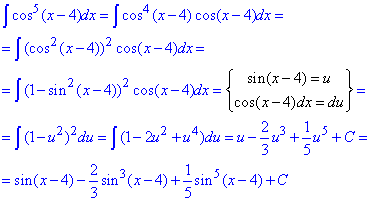
б) Раніше розглядали алгоритмии, як понижувати степінь добутку синусів на косинуси за допомогою тригонометричних формул. Тут маємо приклад з практики, який за кілька перетворень звели до простих табличних інтегралів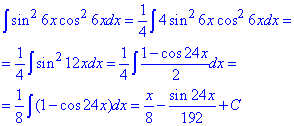
Решта готових відповідей з контрольної роботи на інтеграли Ви знайдете за наведеними нижче посиланнями. Завдання та схеми їх обчислень допоможуть розібратися практично з любим інтегралом.
Готові розв'язки контрольної з інтегрування


