Задачі на зрізану піраміду

Задач на зрізані піраміди не так багато і всі вони основані на теоремах про пропорційні відрізки та подібності фігур. Далі наведено готові розв'язки до задач, які можуть чекати Вас на тестуванні при вступі у ВУЗи, їх взято з наведеного рядом посібника. Школярам 10-11 класів вони також будуть корисними, оскільки розширять практичний багаж знань з геометрії.

Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Тема 37.5 Зрізана піраміда

Задача 37.11 Знайти висоту правильної чотирикутної зрізаної піраміди, у якої сторони основ дорівнюють a і b (a>b), а кут нахилу бічного ребра до більшої основи дорівнює .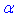

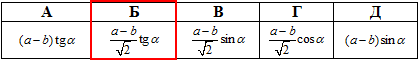
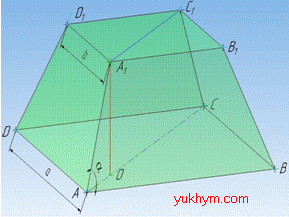
Розв'язання: Маємо завдання на виведення формули висоти.
Нам задано правильну чотирикутну зрізану піраміду ABCDA₁B₁C₁D₁, основами якої є квадрати ABCD і A₁B₁C₁D₁ зі сторонами a та b відповідно.
Діагональним перерізом правильної чотирикутної зрізаної піраміди є рівнобічна трапеція AA₁C₁C з основами AC і A₁C₁ (які є діагоналями основ піраміди – квадратів ABCD і A₁B₁C₁D₁ відповідно).
Бічні сторони AA₁=C₁C є бічними ребрами правильної зрізаної піраміди (вони, за властивістю, є рівними).
Висота A₁O правильної чотирикутної зрізаної піраміди проектується на діагональ основи (квадрата ABCD), а 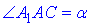– кут нахилу бічного ребра до площини основи, оскільки AO – проекція похилої AA₁ на площину основи.
Діагональ більшої основи (квадрата) ABCD:

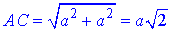
Діагональ меншої основи (квадрата) A1B1C1D1:

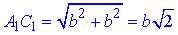
Їх обчислили за допомогою теореми Піфагора у відповідних прямокутних трикутників ABC (∠ABC=90, AB=BC=a) і A₁B₁C₁D₁ (∠A₁B₁C₁=90, A₁B₁=B₁C₁=b).
Розглянемо рівнобічну трапецію AA₁C₁C з основами 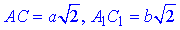, і кутом при основі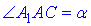

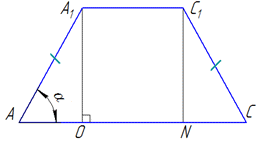
Проведемо висоти A₁O і C₁N, які є висотами зрізаної піраміди.
Прямокутні трикутники рівні ΔA₁AO=ΔC₁CN (за гіпотенузою і катетом), тому відрізки при основі знаходимо зі співвідношення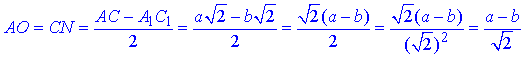
У прямокутному трикутнику A₁AO (∠A₁OA=90) відомо 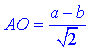– катет, прилеглий до кута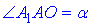
Виходячи з означенням тангенса гострого кута прямокутного трикутника виразимо катет A₁O – висоту зрізаної піраміди:

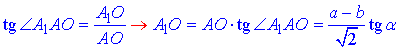
Відповідь: 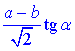– Б.

Задача 37.12 У правильній зрізаній чотирикутній піраміді сторони основи a і b (a>b), двогранний кут при більшій основі – 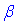. Знайти висоту піраміди.

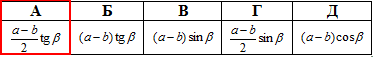
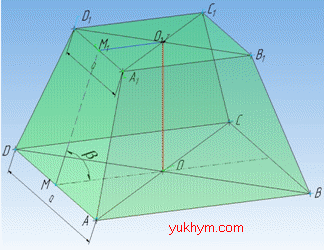
Розв'язання: Умова завдання в певній мірі перекликається з попереднім прикладом, проте хід обчислень відрізняється від того, який наведений вище.
З’єднаємо точки перетину діагоналей обох основ, тоді OO₁ – висота трапеції (властивість правильної чотирикутної піраміди).
Проведемо відрізки OM і O₁M₁, які є перпендикулярними до сторін своїх основ, тобто OM⊥AD, O₁M₁⊥A₁D₁.
За властивістю квадрата (і середньої лінії трикутника)
OM=AB/2=a/2 і O₁M₁=A₁B₁/2=b/2.
Проведемо відрізок MM₁.
Оскільки OM⊥AD, O₁M₁⊥A₁D₁, то за теоремою «про три перпендикуляри» MM₁⊥AD, MM₁⊥A₁D₁.
Звідси слідує, що 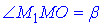– лінійний кут двогранного кута при більшій основі.
Отже, MM₁O₁O – прямокутна трапеція з основами OM=a/2, O₁M₁=b/2 і гострим кутом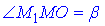
Її рисунок має вигляд

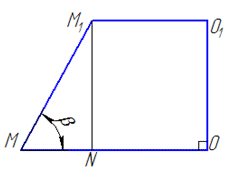
В прямокутній трапеції MM₁O₁O додатково проведемо висоту M₁N (M₁N=OO₁).
Тоді ON=O1M1=b/2, звідси отримаємо

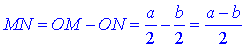
У прямокутному трикутнику MM₁N (∠M₁NM=90) відомо MN=(a-b)/2 – катет, прилеглий до кута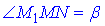
За означенням тангенса гострого кута прямокутного трикутника знайдемо катети M₁N=OO₁ – висоту зрізаної піраміди:

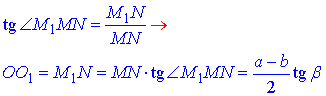
Отримали:
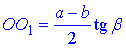– висота зрізаної піраміди.
Відповідь: 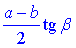– А.

Задача 37.31 Сторони основи правильної зрізаної трикутної піраміди дорівнюють 2 см і 5 см, бічне ребро – 2 см. Знайти у сантиметрах висоту піраміди.

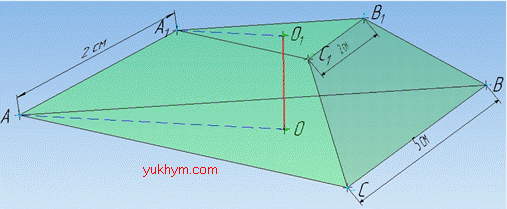
Розв'язання: Маємо правильну зрізану трикутну піраміду ABCA₁B₁C₁, основами якої є рівносторонні трикутники ABC зі стороною a і A₁B₁C₁ зі стороною a1 відповідно.
Оскільки всі бічні ребра піраміди рівні, то основи O і O1 висоти OO₁ є центрами описаних кіл навколо трикутників ABC і A₁B₁C₁ відповідно. Знайдемо радіуси описаних кіл:

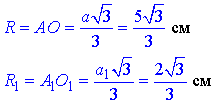
Оскільки висота OO₁ перпендикулярна до площин основи (трикутників ABC і A₁B₁C₁), то вона перпендикулярна до кожної прямої, що лежить в цих площинах, тому OO₁⊥AO і OO₁⊥A₁O₁.
Звідси слідує, що чотирикутник AA₁O₁O – прямокутна трапеція, висота OO₁ якої є висотою зрізаної піраміди.

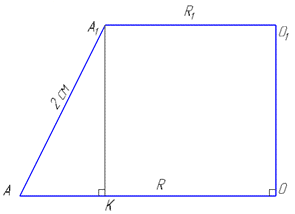
Проведемо відрізок A₁K=O₁O, тобто A₁K⊥AO.
Тут маємо KO=A₁O₁=2√3/3, тоді

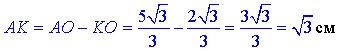
Розглянемо прямокутний трикутник AA₁K (∠AKA₁=90), у якого AA₁=2 см – гіпотенуза (довжина бічного ребра піраміди) і AK=√3 см – катет.
За теоремою Піфагора знайдемо катет A₁K=O₁O – висоту піраміди:

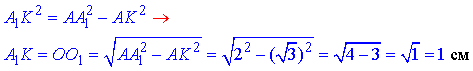
Відповідь: 1.

Подібні завдання вимагають доброго вміння креслити та досконалого володіння теоретичним матеріалом.