Під чотирикутною розуміємо піраміду, в основі якої є чотирикутник. Але чотирикутник це складна фігура, тому тут будуть розглянуті прості приклади, де форма основи є квадратом або прямокутником.
Це значно спрощує обчислення площі бічної поверхні піраміди, її об'єму.
Завдання відповідають шкільній програмі навчання, а також можуть бути використані при ЗНО підготовці.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 37.4 Чотирикутна піраміда
Задача 37.9 Основа піраміди – квадрат зі стороною a. Висота піраміди дорівнює H і проходить через одну з вершин основи. Визначити площу бічної поверхні піраміди.

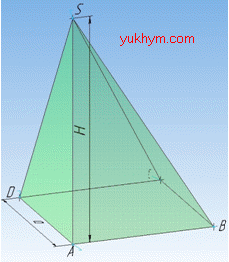
Розв'язання: Площа бічної поверхні піраміди SABCD визначається як сума площ всіх її бічних граней (трикутників):
Sб=SSAD+SSAB+SSDC+SSBC.
За умовою задачі, основою чотирикутної піраміди SABCD є квадрат ABCD зі стороною AB=BC=CD=AD=a, в висота проходить через вершину квадрата, тому SA⊥(ABCD), тобто SA⊥AD і SA⊥AB,, звідси слідує, що трикутники SAD і SAB – прямокутні.
Розглянемо прямокутні трикутники SAD (∠SAD=90) і SAB (∠SAB=90).
В них AD=AB=a і SA=H (як висота піраміди) – катети цих трикутників, тому ΔSAD=ΔSAB (за двома катетами).
Довжини їх гіпотенуз обчислюємо за теоремою Піфагора:
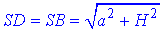
Площа трикутників SAD і SAB:
SSAD=SSAB=aH/2 (півдобуток катетів).
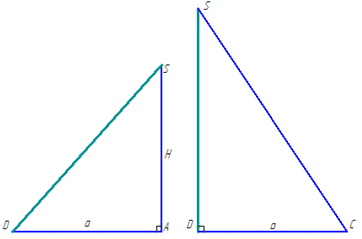
Відрізок SA – перпендикуляр опущений на площину основи піраміди (квадрата ABCD), відрізок SD – похила, а відрізок AD – проекція похилої на площину основи.
Оскільки AD⊥CD, то за теоремою «про три перпендикуляри» (пряма, що перпендикулярна до проекції похилої, перпендикулярна і до самої похилої) маємо SD⊥CD, тому трикутник SDC – прямокутний.
Аналогічно встановлюємо, що трикутник SBC – прямокутний.
Розглянемо прямокутні трикутники SDC (∠SDC=90) і SBC (∠SBC=90).
В них CD=BC=a і 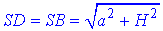 – катети цих трикутників, тому ΔSDC=ΔSBC (за двома катетами).
– катети цих трикутників, тому ΔSDC=ΔSBC (за двома катетами).
Їх площа:
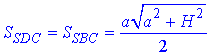 (півдобуток катетів).
(півдобуток катетів).
Площу бічної поверхні піраміди SABCD знаходимо через суму подвійних добутків площ відповідних граней:
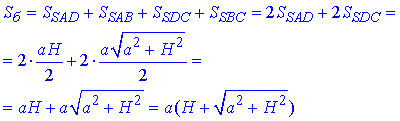
Відповідь: 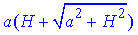 – Г.
– Г.
ЗНО 2018. Завдання 32. У правильній чотирикутній піраміді SABCD сторона основи ABCD дорівнює c, а бічне ребро SA утворює з площиною основи кут α. Через основу висоти піраміди паралельно грані ASD проведено площину β.
1. Побудуйте переріз піраміди SABCD площиною β.
2. Обґрунтуйте вид перерізу.
3. Визначте периметр перерізу.
Розв'язування: 1,2 Побудуємо піраміду SABCD, в основі якої лежить квадрат ABCD.
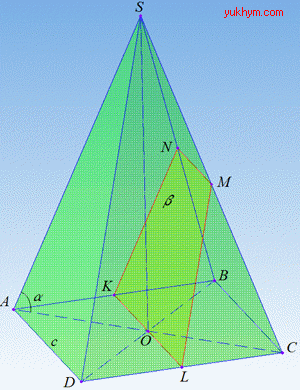
Через точку O, основу висоти піраміди (точку перетину діагоналей AC і BD), проведемо відрізок KL||AD, так як площина β паралельна площині (SAD). З цієї ж умови проведемо відрізки:
NK||SA, ML||SD і послідовно з'єднаємо точки K, L, M , N.
У перерізі піраміди SABCD площиною β отримаємо трапецію KLMN, у якої KL||MN, так як KL||(SAD) і MN||(SAD).
У правильній чотирикутній піраміді SABCD усі бічні грані є рівними рівнобедреними трикутниками, тому NK=ML
(відрізки NK і ML є середніми лініями трикутників SAB і SCD, відповідно). Трапеція KLMN - рівнобічна.
3. За умовою завдання маємо:
AB=BC=CD=AD=c - сторона основи (квадрата) ABCD і ∠SAO=α - кут між ребром SA і площиною основи (квадрата). Відрізок MN з'єднує середини сторін SB і SC, MN||BC, тому MN - середня лінія трикутника SBC.
Тоді отримаємо
KL=AD=c, MN=BC/2=c/2.
Із прямокутного ΔABC знайдемо діагональ AC квадрата ABCD:
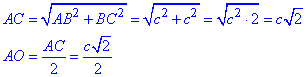
У прямокутному ΔSAO (∠SAO=90), у якого AO=c√2/2 - прилеглий катет до кута ∠SAO=α, за означенням косинуса гострого кута, знайдемо гіпотенузу SA:
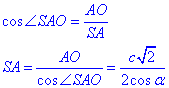
Так як відрізки NK і ML є середніми лініями трикутників SAB і SCD, відповідно, то отримаємо
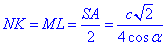
Обчислимо периметр рівнобічної трапеції KLMN:
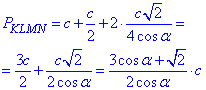
На цьому всі потрібні величини ЗНО тесту знайдено.
Задача 37.10 Висота піраміди поділена на 4 рівні частини і через точки поділу проведено перерізи, паралельні до основи.
Знайти площу найбільшого перерізу, якщо площа основи дорівнює 800 см2.
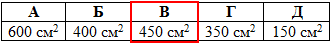
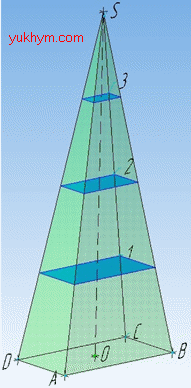
Розв'язання: Площина, яка перетинає піраміду і проходить паралельно основі відтинає подібну піраміду.
А у подібних пірамід відповідні площі відносяться як квадрати їх відповідних лінійних розмірів.
Найбільшу площу має переріз, який знаходиться найближче до основи заданої піраміди (тобто переріз 1), оскільки піраміда з основою, яким є переріз 1 має найбільшу висоту.
Оскільки площини проходять через точки, які ділять висоту заданої піраміди на 4 рівні частини, то висота подібної піраміди з перерізом 1 має висоту
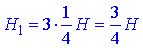
(оскільки вона складається з 3 частин чверті всієї висоти), де H – висота заданої піраміди.
Нехай S=800 см2 – площа основи заданої піраміди, тоді S1 – площа перерізу 1.
Складемо відношення і знайдемо S1:
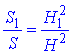
звідси виводимо формулу площі
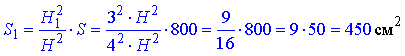
(В задачі не важливо, який многокутник лежить в основі, тому при розв’язуванні на многокутник посилання не було:
це може бути трикутник, чотирикутник (як на рисунку), шестикутник, або будь-який інший многокутник).
Відповідь: 450 см2 – В.
Задача 37.20 Усередині призми з об'ємом V взято довільну точку O й побудовано дві піраміди з вершиною O, що мають основами основи призм.
Знайти суму об'ємів цих пірамід.
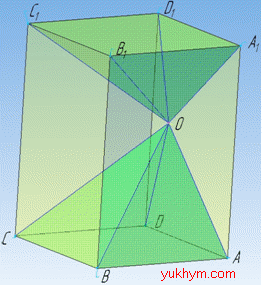
Розв'язання: Нехай V – об'єм заданої призми з площею основи Soc і висотою H;
V1 – об'єм верхньої піраміди з площею основи Soc1 і висотою H1;
V2 – об'єм нижньої піраміди з площею основи Soc і висотою H2.
У призми основи паралельні і рівні, тому площі основи для обох пірамід рівні і дорівнюють площі основи призми Soc.
А висоти обох пірамід в сумі дають висоту призми (H=H1+H2), оскільки вершина O пірамід спільна за умовою задачі.
Тоді сума об'ємів обох пірамід
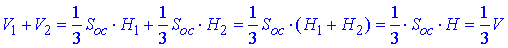
становить третину об'єму заданої призми.
(Ми не вказуємо на вид многокутника, що лежить в основі призми (на рис. це чотирикутник), ні на розташування точки O в середині призмі).
Відповідь: V/3 – Д.
Задача 37.30 Площа основи піраміди дорівнює 72 см2.
Площі двох перерізів, які паралельні до основи, дорівнюють 18 см2 і 50 см2.
Знайти у сантиметрах висоту піраміди, якщо відстань між перерізами дорівнює 8 см.
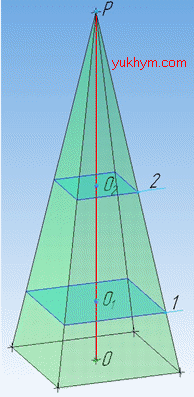
Розв'язання: Маємо піраміду з площею основи Soc=72 см2 і висотою H=PO.
За властивістю: площини, які проходять паралельно основі заданої піраміди, відтинають від неї подібні піраміди.
Тому маємо S1=50 см2 – площа основи (перерізу) І подібної піраміди з висотою H1=PO1 і S2=18 см2 – площа основи (перерізу) ІІ подібної піраміди з висотою H2=PO2.
За умовою задачі відомо, що H1-H2=O1O2=8 см – відстань між перерізами (основами) подібних пірамід.
За властивістю: у побідних пірамід відношення площ основ дорівнює відношенню квадратів їх відповідних лінійних розмірів.
Звідси складаємо відношення для виведення формули висоти піраміди
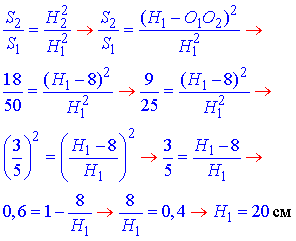
H1=20 см – висота І подібної піраміди.
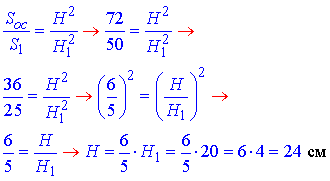
H=24 см – висота заданої піраміди.
Відповідь: 24.
Далі розберемо приклади на зрізану піраміду.



