Задачі на кути в піраміді

Розглянемо кілька готових задач на чотирикутні піраміди, які не увійшли до попередньої статті, де знаходили площу та об'єми.
В наведених прикладах під час обчислень потрібно мати справу з кутами, визначати їх косинуси, тангенси.
Таким чином Ви пригадаєте не тільки теорему Піфагора, а й прості тригонометричні формули.

Задача 37.15 У правильній чотирикутній піраміді двогранний кут при основі дорівнює 45⁰.
Під яким кутом нахилено до площини основи бічне ребро?

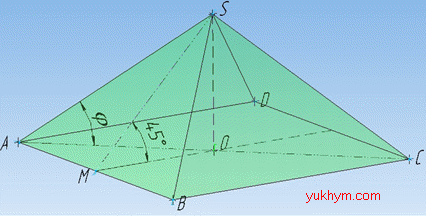
Розв'язання: Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD. Нехай довжина сторони його дорівнює a.
Висота SO правильної трикутної піраміди проектується у центр квадрата ABCD – точку перетину діагоналей AC і BD. Оскільки висота SO перпендикулярна до площини основи (квадрата ADCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥AC.
Відрізок SA – похила, а AO – проекція похилої на площину основи (ΔABC), тому 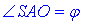– кут нахилу бічного ребра до площини основи.
Проведемо відрізок MO⊥AB і SM. Оскільки MO⊥AB, то за теоремою «про три перпендикуляри» SM⊥AB.
Звідси слідує, що ∠SMO=45 – лінійний кут двогранного кута при основі – кут нахилу бічної грані до площини основи. ∠SOM=90), у якого MO=a/2 (за властивістю квадрата) – катет прилеглий до кута ∠SMO=45.
SO:

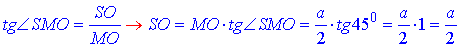
Із прямокутного трикутника ΔAOS у якого SO=a/2 – протилежний катет і AO=a/√2 (половина діагоналі квадрата зі стороною a) – прилеглий катет до 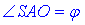, за означенням тангенса гострого кута прямокутного трикутника знайдемо 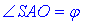– кут нахилу бічного ребра до площини основи:

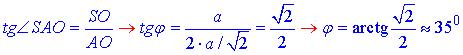
Відповідь: arctan(√2/2) – Д.

Задача 37.23 На рисунку зображено правильну піраміду SABCD, висота якої дорівнює діагоналі основи. Установити відповідність між кутами (1–4) та їхніми градусними мірами (А – Д).

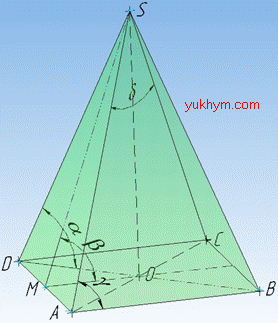
Розв'язання: Маємо чотирикутну піраміду SABCD, в основі якої лежить квадрат ABCD.
Нехай сторона квадрата дорівнює a.
Висота SO правильної чотирикутної піраміди проектується у центр квадрат ABCD, тобто в точку O перетину діагоналей AC і BD.
Діагоналі квадрата рівні: AC=BD=a√2 (за теоремою Піфагора із прямокутного ΔBCD), тоді SO=BD=a√2 (за умовою задачі).
З точки O проведемо відрізок MO перпендикулярно до сторони AD, тобто MO⊥AB. За властивістю квадрата:
MO||BC і MO=BC/2=a/2.
Оскільки висота SO перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥MO і SO⊥DO;
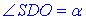– кут нахилу бічного ребра до площини основи.
Проведемо відрізок SM. Оскільки MO⊥AB, то за теоремою «про три перпендикуляри» SM⊥AB. Звідси слідує, що 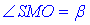– лінійний кут двогранного кута (двогранний кут) при ребрі основі – кут нахилу апофеми (бічної грані) до площини основи.
1) Розглянемо прямокутний трикутник SOD (∠SOD=90), у якого
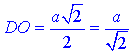– прилеглий катет (половина діагоналі BD) і SO=a√2 – протилежний катет до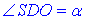
За означенням тангенса гострого кута прямокутного трикутника знайдемо :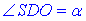

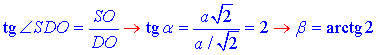
1 – В.

2) Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого MO=a/2 – прилеглий катет і SO=a√2 – протилежний катет до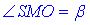
За означенням тангенса гострого кута прямокутного трикутника знайдемо :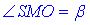

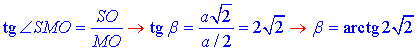
2 – Г.

3) Кут між (мимобіжними) прямими в просторі – кут між прямими, які перетинаються і паралельні до мимобіжних прямих.
Тому кут між прямими SA і DC – це кут між прямими SA і AB (оскільки CD||AB).
Так як 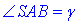– кут між сусідніми бічними ребрами піраміди, то наступні кути рівні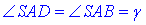
(оскільки у правильній піраміді всі бічні грані (трикутники) рівні.
Розглянемо прямокутний трикутник SMD (∠SMD=90), у якого DM=a/2 – прилеглий катет до 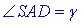і 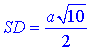– гіпотенуза.
За означенням косинуса гострого кута прямокутного трикутника знайдемо :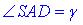
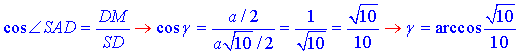
3 – А.

4) Розглянемо трикутник ASC. Оскільки піраміда SABCD – правильна, то всі її бічні ребра рівні SA=SC.
Висота піраміди SO і буде висотою трикутника ASC (як діагонального перерізу), вона ж і буде бісектрисою і медіаною, що проведена сторони основи AC.
Тому 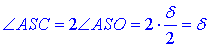(за означенням бісектриси).
Розглянемо прямокутний трикутник ASO (∠AOS=90), у якого 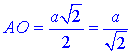– протилежний катет (половина діагоналі AC) і SO=a√2 – прилеглий катет до .
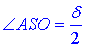За означенням тангенса гострого кута прямокутного трикутника знайдемо

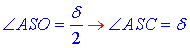
(а звідти і):

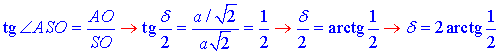
4 – Д.

Задача 37.29 У правильній чотирикутній піраміді бічне ребро утворює з висотою кут 300. Відрізок, що сполучає основу висоти з серединою бічного ребра, дорівнює √3.
Знайти об'єм піраміди.

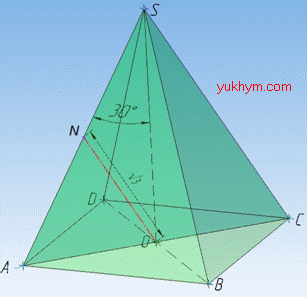
Розв'язання: Об'єм піраміди обчислюється за формулою:

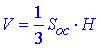
Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить квадрат ABCD.
Висота SO піраміди проектується в центр квадрата – точку O перетину діагоналей AC і BD.
У правильній піраміді всі бічні ребра рівні, тому трикутник ASC – рівнобедрений з основою AC і бічними сторонами SA=SC.
Оскільки трикутник ASC є діагональним перерізом піраміди, то висота піраміди SO є висотою трикутника ASC проведеної до основи AC, а за властивістю рівнобедреного трикутника, бісектрисою і медіаною.
Звідси, ∠ASO=30 за умовою задачі, ∠ASC=60 (за означенням бісектриси SO).
Тоді за сумою кутів ΔASC і властивості кутів при основі у рівнобедреного ΔASC маємо:

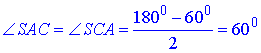
звідси слідує, що ΔASC – рівносторонній.
Відрізок NO=√3 (за умовою) є середньою лінією ΔASC, оскільки сполучає середини сторін AC і SA.
Тому відрізок NO відтинає подібний (а значить рівносторонній) ΔAON, звідси AO=AN=NO=√3.
Тоді AC=2AO=2√3 – довжина діагоналі квадрата ABCD, SA=SC=2AN=2√3 – довжина бічного ребра.
Площа основи (квадрата) ABCD піраміди:
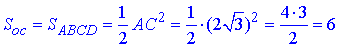Із прямокутного трикутника ΔASO (∠SOA=90), у якого AO=√3 – протилежний катет до ∠ASO=30 за означенням тангенса гострого кута прямокутного трикутника знайдемо прилеглий катет SO – висоту піраміди:

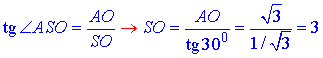
Об'єм правильної чотирикутної піраміди:

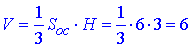
Відповідь: 6.

Задача 37.33 У правильній піраміді площа основи становить 1/3 площі повної поверхні.
Знайти у градусах двогранний кут при основі піраміди.

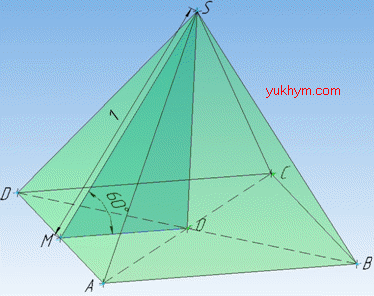
Розв'язання: У правильній піраміді основа – правильний многокутник (у якого всі сторони і кути рівні), а бічні грані – рівні між собою рівнобедрені трикутники.
Висота правильної піраміди проектується в центр описаного навколо і вписаного в многокутник кола.
Якщо провести радіуси описаного кола з центра основи піраміди з площею Soc у дві сусідні вершини многокутника, то отримаємо рівнобедрений трикутник з площею Soc/n, який є проекцією бічної грані з площею Sб/n на площину основи.
Таких трикутників у многокутнику буде n штук, що відповідає кількості сторін многокутника (і кількості бічних граней піраміди).
За теоремою «про площу ортогональної проекції многокутника» маємо співвідношення:
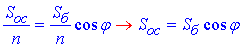(1)
де phi – кут між бічною гранню і основою піраміди, двогранний кут при основі.
Але Sпп=Soc+Sб, звідси Sб=Sпп-Soc.
За умовою задачі:
Soc=Sпп/3, тобто 3Soc=Sпп, звідси Sб=Sпп-Soc=2Soc.
Отже Sb=2Soc.
Підставимо вираз у співвідношення (1), отримаємо

Відповідь: 60⁰.

(В ході розв'язку задачі не має посилання на вид многокутника (на рис. це чотирикутник); за такою схемою можна було розв'язати задачі 37.2, 37.16 і 37.17).

Задача 37.2 Сторона основи правильної чотирикутної піраміди дорівнює a. Бічна грань нахилена до площини основи під кутом .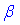
Визначити апофему піраміди.

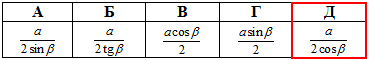
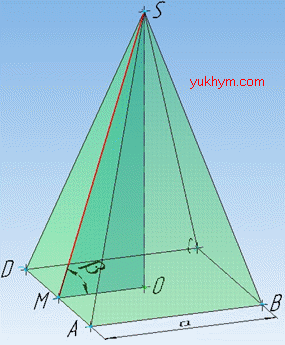
Розв'язання: В основі правильної чотирикутної піраміди SABCD може бути тільки правильний чотирикутник (квадрат) ABCD зі стороною a (за умовою задачі).

Всі бічні грані правильної піраміди нахилені під однаковим кутом 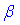до площини основи, тому вершина піраміди проектується в центр основи піраміди (в точку перетину діагоналей квадрата), звідси SO – висота піраміди.
Проведемо відрізок MO⊥AD. Оскільки висота SO піраміди перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що належить площині основи, тому SO⊥MO.
Проведемо відрізок (похилу) SM. Оскільки MO⊥AD, то за теоремою «про три перпендикуляри» маємо SM⊥AD.
Звідси SM – висота бічної грані правильної чотирикутної піраміди – апофема піраміди;
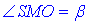– кут нахилу бічної грані до площини основи.
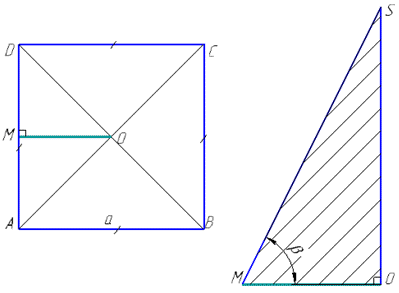
У квадраті MO⊥AD, де точка O – центр квадрата (точка перетину діагоналей), тому (за властивістю квадрата)
MO||AB і MO=AB/2=a/2 (це доводиться на основі того, що MO – середня лінія трикутника ACD).
Розглянемо прямокутний трикутник MOS (∠MOS=90), в якому MO=a/2 – катет прилеглий до кута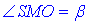
З означення косинуса гострого кута прямокутного трикутника виразимо гіпотенузу SM – апофему піраміди:

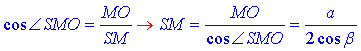
Відповідь: 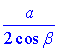– Д.

Попереду на Вас чекають нові тестові задачі де також будемо знаходити площі пірамід, об'єм, виводити певні формули з пропорцій.
Після доброго аналізу практичної частини, що тут наведена, Ви легко зможете пройти подібні тести.