Сьогодні розпочнемо аналізувати готові задачі на піраміди. Їх, як і завдання на призми взято із посбника для підготовки до ЗНО з математики. Всього розв'язано 35 прикладів і погруповано на менші підтеми: трикутні, чотирикутні та зрізані піраміди. Завдання вимагають добрих знань геометричних фігур, тригонометричних формул та вміння креслити. Все це Ви повинні вчити на уроках геометрії в 10-11 класі.
Без просторової уяви Вам важко буде виконати наведену далі побудову до умов завдань, а отже не зможете розібратися, що від Вас вимагають. Уважно аналізуйте відповіді та використовуйте отримані знання у навчанні.
Ви можете безкоштовно завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 37.1 Правильна трикутна піраміда
Задача 37.1 Сторона основи правильної трикутної піраміди дорівнює b√3, а висота піраміди – H. Визначити бічне ребро піраміди.
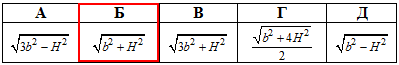
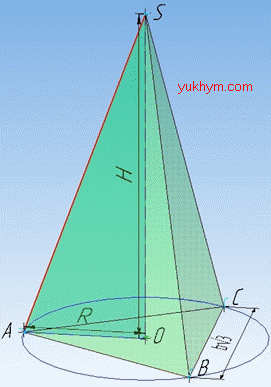
Розв'язання: В основі правильної трикутної піраміди SABC лежить правильний (рівносторонній) трикутник ABC зі стороною b√3.
Всі ребра правильної піраміди рівні, проекцією вершина піраміди є центр описаного навколо основи кола.
Позначимо:
SO – висота піраміди,
AO – радіус описаного кола;
SA – бічне ребро піраміди.
Оскільки висота SO піраміди перпендикулярна до площини основи (трикутника ABC), то вона перпендикулярна до кожної прямої, що належить площині основи, тому SO⊥AO.
У рівносторонньому трикутнику ABC (AB=AC=BC=b√3) знайдемо радіус описаного кола AO=R:
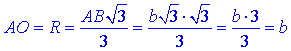
Розглянемо прямокутний трикутник AOS (∠AOS=90), у якому AO=b, SO=H – катети.
За теоремою Піфагора знайдемо гіпотенузу SA – довжину бічного ребра правильної трикутної піраміди:
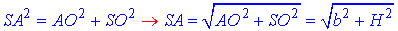
На цьому задача розв'язана.
Відповідь: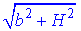 
– Б.
Задача 37.3 Сторона основи правильної трикутної піраміди дорівнює 6 см, а бічне ребро – 5 см. Знайти бічну поверхню піраміди.
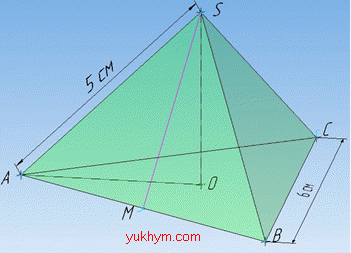
Розв'язання: Бічну поверхню (тобто її площу) правильної трикутної піраміди SABC обчислюють за формулою:
Sб=Poc•l, де Poc – периметр основи (трикутника ABC);
l=SM – апофема, висота бічної грані.
Периметр основи (правильного трикутника ABC) зі стороною AB=BC=AC=6 см:
Poc=AB+BC+AC=6+6+6=18 см.
Розглянемо бічну грань SAB.
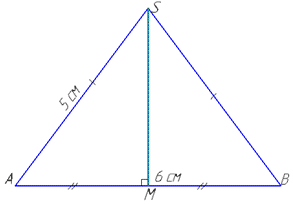
Оскільки у правильної піраміди всі бічні ребра рівні, то трикутник SAB – рівнобедрений з основою AB=6 см і бічними сторонами SA=SB=5 см.
Проведемо висоту бічної грані SM – апофему піраміди до сторони основи AB, SM⊥AB.
За властивістю рівнобедреного трикутника:
SM – медіана і бісектриса ΔSAB, звідси маємо AM=MB=3 см.
У прямокутному трикутнику SAM (∠SMA=90) відомо SA=5 см – гіпотенуза, AM=3 см – катет.
За теоремою Піфагора знайдемо катет SM=l:
SM2=SA2-AM2, звідси
Площу бічної поверхні правильної трикутної піраміди знаходимо за формулою:
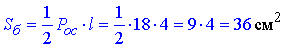
Відповідь: 36 см2 – В.
Задача 37.13 Ребро правильного тетраедра дорівнює a.
Визначити об'єм тетраедра.
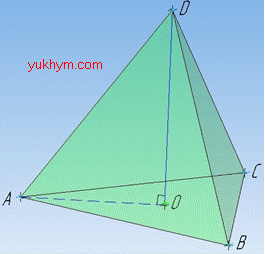
Розв'язання: Об'єм тетраедра (як і будь-якої піраміди) обчислюють за формулою:
V=1/3•Soc•H,
де Soc=SABC – площа основи (трикутника ABC);
H=DO – висота тетраедра.
Тетраедр ABCD – трикутна піраміда, всі ребра якої рівні і дорівнюють a.
Тому в основі лежить правильний (рівносторонній) трикутник зі стороною a.
Звідси площу основи знаходимо за формулою для рывностороннього трикутника:
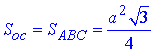
Оскільки тетраедр – правильна трикутна піраміда, то висота DO проектується в центр описаного навколо трикутника ABC кола, радіус якого рівний
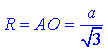
Висота тетраедра DO перпендикулярна до площини основи (трикутника ABC), тому вона перпендикулярна до кожної прямої, що лежить в площині основи.
Звідси DO⊥AO, тому трикутник AOD (∠AOD=90) – прямокутний.
В ньому відома AD=a – гіпотенуза (довжина ребра тетраедра) і AO=a/√3 – катет.
За теоремою Піфагора обчислимо катет DO – висоту тетраедра:
DO2=AD2-AO2,
звідси
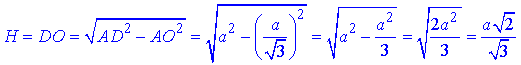
Об'єм тетраедра:
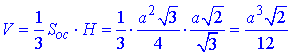
Відповідь: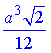 
– А.
Задача 37.14 У правильній трикутній піраміді бічне ребро нахилено до площини основи під кутом 600.
Під яким кутом нахилена до площини основи бічна грань?
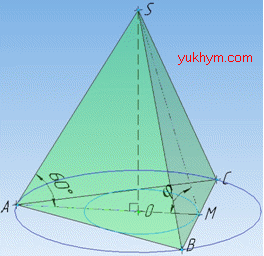
Розв'язання: Маємо правильну трикутну піраміду SABC, в основі якої лежить правильний (рівносторонній) трикутник ABC. Нехай довжина його сторони рівна a.
Висота SO правильної трикутної піраміди проектується у центр вписаного в трикутник ABC і описаного навколо трикутника ABC кола (адже в рівносторонньому трикутнику ABC вони співпадають).
Звідси слідує, що радіус описаного навколо ΔABC кола рівний
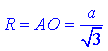
радіус вписаного кола
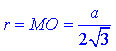
За властивістю радіуса вписаного кола:
MO⊥BC.
Оскільки висота SO перпендикулярна до площини основи (трикутника ABC), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥AM.
Відрізок SA – похила, а AO – проекція похилої на площину основи (ΔABC), тому ∠SAO=60 – кут нахилу бічного ребра до площини основи.
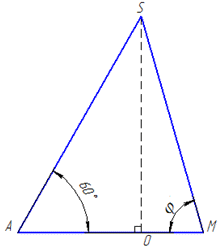
Проведемо відрізок SM. Оскільки OM⊥BC, то за теоремою «про три перпендикуляри» SM⊥AD.
Звідси слідує, що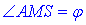 
– лінійний кут двогранного кута при основі – кут нахилу бічної грані до площини основи.
Розглянемо трикутник ASM, у якого SO є висотою, тому ΔAOS і ΔMOS – прямокутні (∠AOS=90 і ∠MOS=90 відповідно).
Із прямокутного ΔAOS, у якого AO=a/√3 – катет прилеглий до ∠SAO=60, за означенням тангенса гострого кута прямокутного трикутника знайдемо протилежний катет SO:
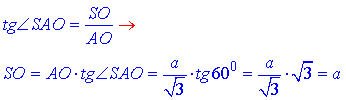
Із прямокутного трикутника ΔMOS сторона SO=a – протилежний катет і MO=a/(2√3) прилеглий катет до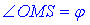 
.
За означенням тангенса гострого кута прямокутного трикутника знайдемо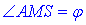 
– кут нахилу бічної грані до площини основи:
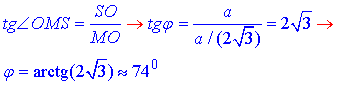
Відповідь: arctan(2√3) – Б.
Задача 37.16 Площа основи правильної трикутної піраміди дорівнює S, а площа бічної поверхні – Q. Визначити двогранний кут при основі.
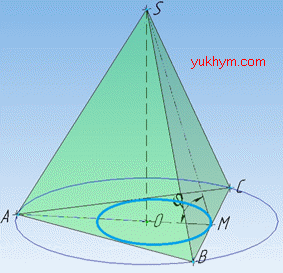
Розв'язання: Маємо правильну трикутну піраміду SABC, в основі якої лежить правильний трикутник ABC.
Позначимо довжину сторони ΔABC через a.
Тоді площа рівностороннього трикутника можна записати формулою
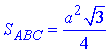
але за умовою задачі SABC=S, звідси отримаємо залежність сторони через площу
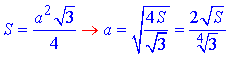
Площа бічної поверхні правильної трикутної піраміди:
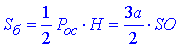
але за умовою задачі Sб=Q, з цієї умови виражаємо висоту піраміди
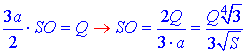
Висота SO правильної трикутної піраміди проектується у центр вписаного в трикутник ABC і описаного навколо трикутника ABC кола
(адже в рівносторонньому трикутнику ABC вони співпадають).
Звідси знаходимо радіус вписаного в трикутник ΔABC кола
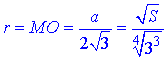
За властивістю радіуса вписаного кола:
MO⊥BC.
Оскільки висота SO перпендикулярна до площини основи (трикутника ABC), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥AM.
Проведемо відрізок SM.
Оскільки OM⊥BC, то за теоремою «про три перпендикуляри» SM⊥AD.
Звідси слідує, що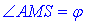 
– двогранний кут при основі – кут нахилу бічної грані до площини основи.
Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого відомі
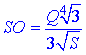– протилежний катет і
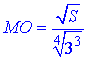– прилеглий катет до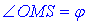 
Двогранний кут при основі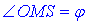 
знайдемо з означенням тангенса гострого кута прямокутного трикутника :
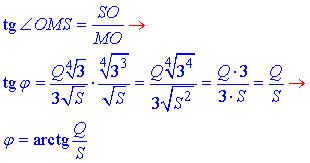
Після спрощень отримаємо арктангенс, який відповідає варіанту Б тестів.
Відповідь: arctan(Q/S) – Б.
Задача 37.19 Сторона основи правильної трикутної піраміди дорівнює a, а площа перерізу піраміди площиною, яка проходить через бічне ребро і перпендикулярна до основи, дорівнює Q. Знайти об'єм піраміди.
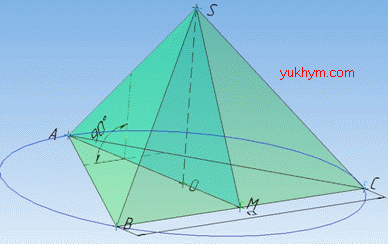
Розв'язання: Об'єм правильної трикутної піраміди SABC обчислюють за формулою:
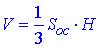
тут
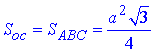
формула площі основи (правильного ΔABC) зі стороною a;
H=SO – висота піраміди і ΔASM одночасно,
адже площина (ΔASM) перпендикулярна до площини основи (ΔABC) за умовою задачі, тому SO⊥AM.
Висота SO правильної трикутної піраміди проектується у центр вписаного в трикутник ABC і описаного навколо трикутника ABC кола (адже в рівносторонньому трикутнику ABC вони співпадають).
Звідси слідує, AM=a√3/2 – довжина висоти (бісектриси і медіани) в рівносторонньому ΔABC. Знайдемо площу трикутника ΔASM:
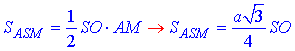
Але за умовою задачі вона рівна SASM=Q.
Звідси отримуємо умову та виводимо формулу висоти піраміди
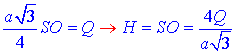
Далі все підставляємо в формулу об'єму трикутної піраміди SABC:
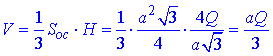
Відповідь: Q•a/3 – Б.
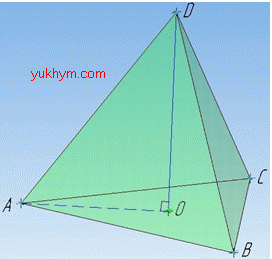
Задача 37.24 На рисунку зображено правильну трикутну піраміду SABC, у якої:
SO – висота; SM – апофема; сторона основи дорівнює a; бічна грань нахилена до площини основи під кутом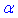 
.
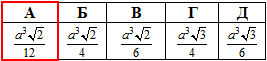
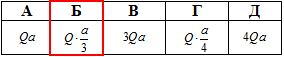
Установити відповідність між сторонами піраміди (1–4) та їхніми величинами (А – Д).
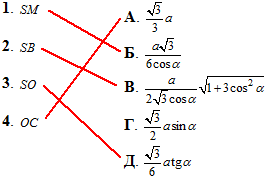
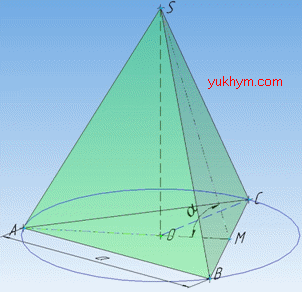
Розв'язання: Задано правильну трикутну піраміду SABC, в основі якої лежить правильний (рівносторонній) трикутник ABC зі стороною a.
Висота SO правильної трикутної піраміди проектується у центр вписаного в трикутник ABC і описаного навколо трикутника ABC кола.
Звідси маємо дві формули
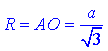– радіус описаного навколо ΔABC кола;
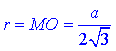– радіус вписаного в ΔABC кола.
За властивістю радіуса вписаного кола:
MO⊥BC. Оскільки висота SO перпендикулярна до площини основи (трикутника ABC), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥AM.
Проведемо відрізок SM. Оскільки OM⊥BC, то згідно теореми «про три перпендикуляри» справедлива залежність SM⊥AD. Звідси слідує, що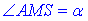 
– лінійний кут двогранного кута при основі – кут нахилу бічної грані до площини основи.
1) Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого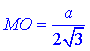 
– катет прилеглий до кута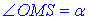 
За означенням косинуса гострого кута прямокутного трикутника визначимо гіпотенузу SM– апофему піраміди SABC:
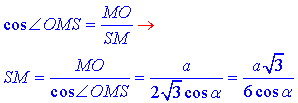
1 – Б.
2) Розглянемо прямокутний трикутник SBM (∠SMB=90), у якого
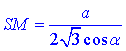і BM=a/2
(оскільки AM медіана, висота і бісектриса у рівносторонньому ΔABC) – катети .
За теоремою Піфагора знайдемо довжину гіпотенузи SB – довжину бічного ребра піраміди SABC:
SB2=SM2+BM2, звідси
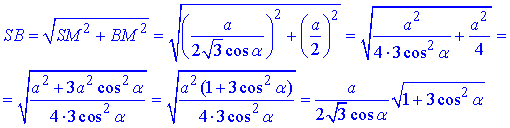
2 – В.
4) SOM(∠SOM=90), у якого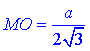 
– прилеглий катет до 
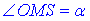, за означенням тангенса гострого кута прямокутного трикутника знайдемо катет SO – висоту піраміди SABC:
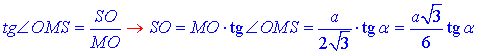
3 – Д.
4) Оскільки точка O – центр описаного навколо ΔABC кола, то відрізок OC – радіус описаного навколо ΔABC кола:
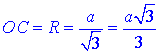
4 – А.
Задача 37.26 Установити відповідність між довжиною ребра (1–4) тетраедра та його об'ємом (А – Д).
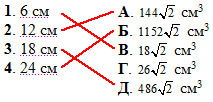
Розв'язання: Розв'язок цієї задачі розписаний у номері 37.13. Там отримана формула для обчислення об'єму тетраедра
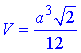
Її ми застосовуємо для кожного випадку:
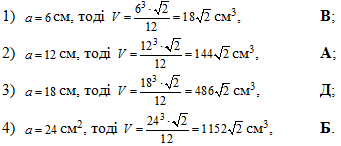
Далі наведені розв'язки задач на чотирикутні та зрізані піраміди.
