Сьогодні розглянемо 6 останніх прикладів з 25 на рівнобедрені трикутники, які відібрані з наведеного далі збірника для підготовки до ЗНО.
Подібні завдання Ви обов'язково розв'язували на практичних з геометрії у 8, 9, 10 класах.
Ви можете завантажити без реєстрації відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Зміст: Посібник містить поради щодо проходження ЗНО з математики та подібні до тестових завдання.
Усі задачі однієї теми розміщені в порядку зростання складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 31. Рівнобедрені трикутники
Приклад 31.20 S – площа рівностороннього трикутника.
Серед наведених графіків указати графік залежності периметра P від S: P=P(S). 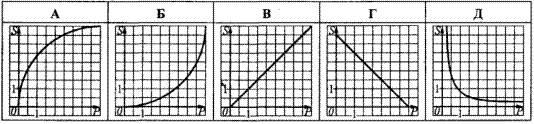 Обчислення: З курсу геометрії відома формула P=3a – периметру рівностороннього трикутника,
Обчислення: З курсу геометрії відома формула P=3a – периметру рівностороннього трикутника,
Площа рівностороннього трикутника виражається формулою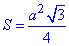
Звідси виводимо формулу площі через периметр 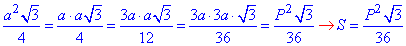
Отримали квадратичну залежність площі від периметра.
Серед наведених графіків вибираємо єдиний, що містить квадратичну функцію.
Відповідь: Б.
Приклад 31.21 На рисунку зображено рівнобедрений трикутник ABC (AC=BC), його висоту AD і позначено величини деяких його елементів.
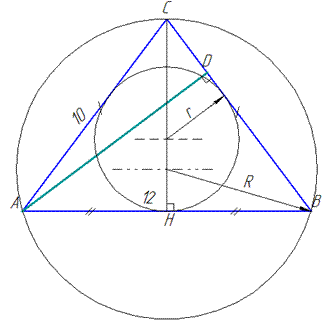 Установити відповідність між елементами трикутника (1–4) та їхніми величинами (А – Д).
Установити відповідність між елементами трикутника (1–4) та їхніми величинами (А – Д).
1. AD
2. SΔABC
3. Радіус вписаного кола
4. Радіус описаного кола
А. 9,6
Б. 6,25
В. 3
Г. 48
Д. 32
Обчислення: У рівнобедреному ΔABC відомо:
AC=BC=10, AB=12, CH⊥AB, AD⊥BC, де AC і BC – бічні сторони, AB – основа;
CH, AD – висоти рівнобедреного ΔABC, які проведені до сторін AB і BC, відповідно.
За властивістю медіани, яка проведена до основи у рівнобедреному трикутнику (це висота і бісектриса), маємо AH=HB=AB/2=12/2=6.
У прямокутному трикутнику ACH (∠AHC=90) знайдемо катет CH:
AH^2+CH^2=AC^2, звідси 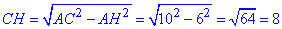
Площа рівнобедреного трикутника ABC:
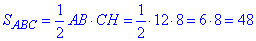 2 – Г.
2 – Г.
Висота AD, яка проведена до бічної сторони BC:
на основі формули площі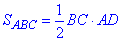
знайдемо висоту
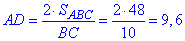 1 – А
1 – А
Радіус вписаного кола r рівний відношенню площі до півпериметра:
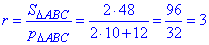 3 – В
3 – В
Радіус описаного кола R знаходимо за формулою:
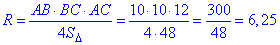 4 – Б.
4 – Б.
Приклад 31.22 Установити відповідність між заданими довжинами основ (1–4) рівнобедрених трикутників з кутами 1200 при вершинах, протилежних до основ, та їх висотами (А – Д) до основ.
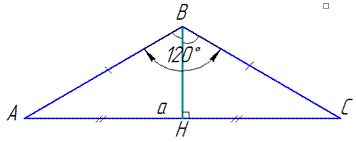
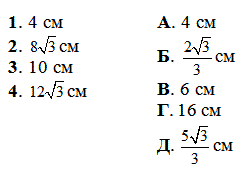
Обчислення: У рівнобедреному ΔABC маємо:
AC=a см, AB=BC, ∠ABC=120, BH⊥AC, де AB і BC – бічні сторони, AC– основа і BH – висота рівнобедреного ΔABC. За властивістю медіани, яка проведена до основи у рівнобедреному трикутнику (це висота і бісектриса), маємо AH=HC=AC/2=a/2см, ∠ABH=60.
У прямокутному трикутнику ABH ( ∠AHB=90) знайдемо катет BH за означенням тангенса гострого кута прямокутного трикутника:
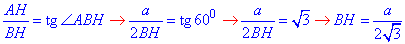
Звідси, отримаємо наступні значення висот BH (для кожного значення AC=a):
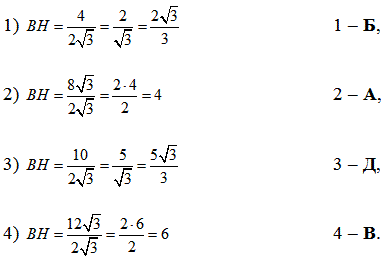
Приклад 31.23 Установити відповідність між довжинами бічних сторін рівнобедрених трикутників (1–4), кут між якими дорівнює 30 градусів, та площами (А – Д) цих трикутників.
1. 20 см
2. 24 см
3. 28 см
4. 32 см
А. 196 см2
Б. 100 см2
В. 256 см2
Г. 625 см2
Д. 144 см2
Обчислення: Нехай бічна сторона трикутника дорівнює a см, а кут між бічними сторонами 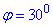
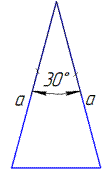 Тоді площа будь-якого трикутника обчислюється за формулою (тобто за двома сторонами a і кутом між ними phi=30):
Тоді площа будь-якого трикутника обчислюється за формулою (тобто за двома сторонами a і кутом між ними phi=30):
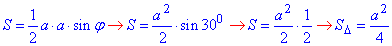
Отож, обчислимо площі трикутників залежно від довжини бічної сторони a:
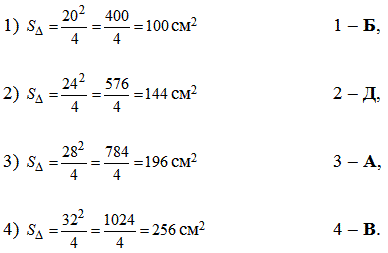
Приклад 31.24 Установити відповідність між довжинами сторін рівнобедрених трикутників (1–4) та радіусами описаних навколо них кіл (А–Д).
1. 29 см, 29 см, 42 см
2. 30 см, 30 см, 48 см
3. 5 см, 5 см, 8 см
4. 20 см, 20 см, 32 см
А. 21,025 см
Б. 20 см
В. 25 см
Г. 25/6 см
Д. 50/3 см.
Обчислення: Радіус кола R, описаного навколо рівнобедреного трикутника (з бічними сторонами a та основою b) обчислюють за формулою:
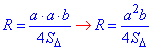
Площу рівнобедреного трикутника S обчислимо за формулою Герона:
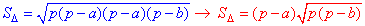
де p=(2a+b)/2 – півпериметр рівнобедреного трикутника.
Отже,
1.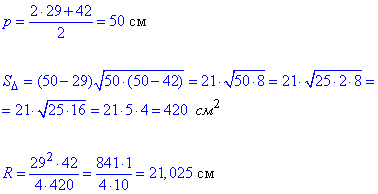 – А
– А
2. 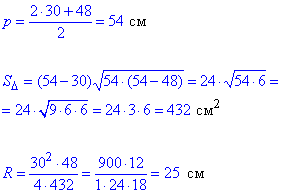 – В
– В
3. 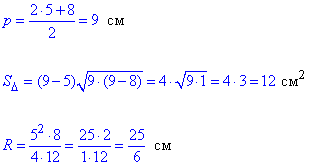 – Г
– Г
4. 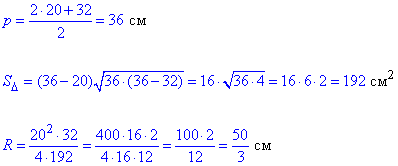 – Д.
– Д.
Приклад 31.25 Периметр рівнобедреного трикутника дорівнює 20.
Знайти його основу, якщо вона на 2 більша від бічної сторони.
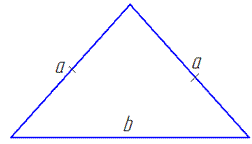 Обчислення: Нехай у рівнобедреному трикутнику маємо бічні сторони довжиною a і основу b, тоді периметр трикутника:
Обчислення: Нехай у рівнобедреному трикутнику маємо бічні сторони довжиною a і основу b, тоді периметр трикутника:
PΔ=2a+b, звідси 2a+b=20 (*).
Але за умовою задачі: b-a=2 (**).
Отримаємо систему з двох рівнянь (*) і (**), з двома невідомими (a і b).
Розв'яжемо цю систему і знайдемо основу b рівнобедреного трикутника:
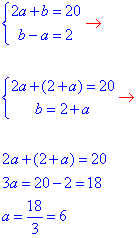
a=6 – бічна сторона рівнобедреного трикутника,
b=a+2=8 – основа рівнобедреного трикутника.
Відповідь: 8.
На цьому завершуються пояснення до тестових прикладів на рівнобедрені трикутники.
Кому пояснень недостатньо для підготовки до ЗНО з математики, може переглянути додатково ще 300 готових відповідей до завдань з трикутниками в категорії геометрія.



