 Є більше 5 формул на знаходження площі трапеції, пригадаємо поширені з них.
Є більше 5 формул на знаходження площі трапеції, пригадаємо поширені з них.
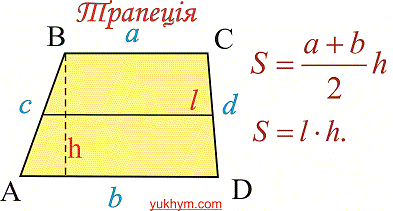
За першою основною формулою, площа трапеції рівна добутку півсуми основ на висоту:
S=(a+b)/2*h.
Якщо врахувати, що сере лінія трапеції рівна півсумі основ l=(a+b)/2, то попередню формулу площі можна записати у вигляді:
S=l*h.
Якщо відомі діагоналі трапеції та кут між ними, або їх можна визначити то площу трапеції обчислюють як півдобуток діагоналей трапеції на синус кута між ними
S=d1*d2*sin(alpha); S=d1*d2*sin(beta).
Окрім наведених, ще є формули Герона для площі трапеції коли відомі всі 4 сторони трапеції; основа трапеції, сторона та кут між ними; для рівнобічних трапецій радіус вписаного кола і інші формули. Далі розглянемо завдання ЗНО тестів на знаходження площі трапеції.
Обчислення площі трапеції. ЗНО відповіді
Подібні завдання Вам можливо доводилося розв'язувати в 8, 9 чи 10 класі, але пригадати формули та властивості трапеції краще всього на готових розв'язках, а їх тут багато.
Приклад 32.37 Основи трапеції дорівнюють 10 і 24, а бічні сторони – 15 і 13. Знайти площу трапеції.
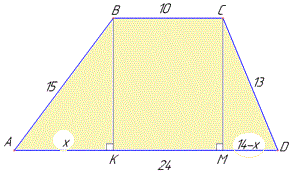
Розв'язування: Нехай заданомо трапецію ABCD (AD||BC), у якої BC=10 і AD=24 - основи; AB=15 і CD=13 - бічні сторони (за умовою). Проведемо висоти BK і CM до сторони AD (BK⊥AD, CM⊥AD, BK=CM). Рисунок трапеції до умови наведено нижче
Це завдання можна розв'язати двома способами, подумайте про другий варіант.
Позначимо: AK=x, тоді MK=BC=10 і MD=14-x
(тут AD=AK+MK+MD=x+10+(14-x)=24).
У прямокутному трикутнику ΔABK (∠K=90) за теоремою Піфагора запишемо висоту через гіпотенузу AB та частину основи трапеції:
BK^2=AB^2-AK^2=15^2-x^2=225-x^2.
Аналогічні формули за теоремою Піфагора отримаємо для прямокутного трикутника ΔCDM (∠M=90):
CM^2=CD^2-MD^2=13^2-(14-x)^2=-27+28x-x^2.
Оскільки висоти трапеції рівні між собою BK=CM (тобто BK^2=CM^2), то можемо записати рівняння
225-x^2=-27+28x-x^2,
28x+x^2-x^2=225+27,
28x=252,
x=9.
Отже, AK=9 і MD=5. Тоді обчислимо висоту трапеції:
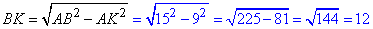 .
.
Обчислимо площу трапеції через добуток півсуми основ на висоту:
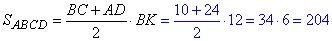
Відповідь: 204.
Приклад 32.38 У прямокутному трикутнику ABC точка M є серединою гіпотенузи AB, довжина якої дорівнює 26 см. Точка O віддалена від вершин B і C на 15 см, а від сторони BC - на 10√2см. З точки O на катет BC опущено перпендикуляр OK, точка K належить відрізку OM. Довести, що чотирикутник KMAC є трапецією. Визначити площу трапеції KMAC.
Розв'язування: Щоб краще уявити, що задано і що потрібно знайти в геометричних задачах старайтеся виконувати рисунки до умови. Побудуємо трикутник та задану точку
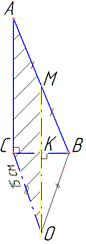
У прямокутному трикутнику ABC (∠ACB=90) відомі AB=26 см – гіпотенуза, AC і BC - катети. А також AM=BM=AB:2=26:2=13 см (за умовою).
Розглянемо рівнобедрений трикутник ΔBOC, у якого OB=0C=15 см - бічні сторони (відстань від точки O до вершин B і C), OK=10√2 см - висота, що проведена до основи BC (OK⊥BC) - відстань від точки O до сторони BC. Тоді відрізок OK - є медіаною і бісектрисою, тому BK=CK. У прямокутному трикутнику ΔKOC (∠K=90) за теоремою Піфагора знайдемо катет CK:
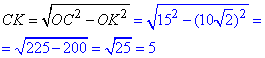
Звідси слідує, що BK=CK=5 см і BC=2•CK=2•5=10 см.
Оскільки точка M - середина сторони AB, точка K - середина сторони BC, то відрізок MK - середня лінія ΔABC, тому за властивістю: MK||AB і чотирикутник KMAC - трапеція, що і треба було довести.
У прямокутному ΔABC (∠ACB=90) за теоремою Піфагора знайдемо катет AC:
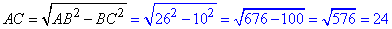 см.
см.
За властивістю середньої лінії трикутника ΔABC маємо:
MK=AC:2=24:2=12 (см).
У трапеції KMAC отримали: AC=24 см, MK=12 см - основи, а CK=5 см - висота.
Знайдемо площу трапеції KMAC за формулою:
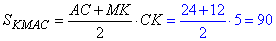
Відповідь: 90.
Уважно перечитайте пояснення до задачі, такі приклади часто зустрічаються на ЗНО тестах.
Приклад 32.39 Основи трапеції дорівнюють 5 і 15, а діагоналі – 12 і 16. Знайти площу трапеції.
Розв'язування: Нехай маємо трапецію ABCD (AD||BC), у якої BC=5 і AD=15 - основи;
AC=16 і BD=12 - діагоналі (за умовою), які перетинаються в точці O. Проведемо висоту MK до сторін AD і BC (MK⊥AD, MK⊥BC).
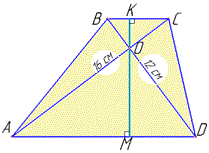
Розглянемо ΔCOB і ΔAOD, у яких кути при вершині O рівні як вертикальні, а також ∠OBC=∠ODA і ∠OCB=∠OAD як внутрішні різносторонні при паралельних прямих BC, AD і січних AC, BD, відповідно. Звідси слідує, що ΔCOB і ΔAOD подібні, тому їх відповідні сторони пропорційні. Отже, - для діагоналі AC маємо:
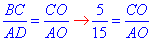
отримали AO=3CO і
AC=AO+CO=3CO+CO=4C0=16,
звідси CO=16:4=4 і AO=12;
- для діагоналі BD маємо:
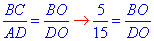
отримали DO=3BO і
BD=BO+DO=BO+3BO=4BO=12,
звідси B0=12:4=3 і DO=9.
За теоремою Піфагора встановлюємо, що трикутники ΔCOB і ΔAOD - прямокутні, з прямим кутом при вершині O:
- для ΔCOB маємо:
BC^2=BO^2+CO^2, 5^2=3^2+4^2 - рівність виконується;
- для ΔAOD маємо:
AD^2=AO^2+DO^2, 15^2=12^2+9^2 - рівність виконується.
У прямокутному трикутнику ΔCOB, із формул площі складемо рівняння, з якого знайдемо висоту KO:

Аналогічним чином для прямокутного трикутника ΔAOD через площу знайдемо висоту MO:
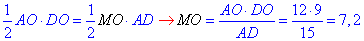
Звідси, MK=KO+MO=2,4+7,2=9,6 - довжина висоти трапеції ABCD.
Обчислюємо площу трапеції як добуток півсуми основ на висоту:
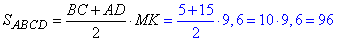
Відповідь: 96.
Приклад 32.41 Площі трикутників, утворених основами трапеції та відрізками діагоналей дорівнюють S1 і S2. Визначити площу трапеції й обчислити її значення, якщо S1=4, S2=1.
Розв'язування: Нехай маємо трапецію ABCD (AD||BC), діагоналі AC, BD якої перетинаються в точці O і утворюють трикутники AOD і BOC з площами S1 і S2, відповідно (за умовою). Через точку O проведемо висоту MN трапеції ABCD до основ AD і BC (MN⊥BC, MN⊥AD). Намалюємо трапеції і заштрихуємо площі трикутників з умови
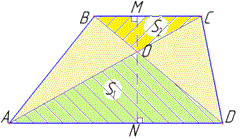
Позначимо висоти трикутників: MO=h2 і NO=h1, причому MN=NO+MO=h1+h2.
Розглянемо трикутники ΔCOB і ΔAOD, у яких кути при вершині O рівні як вертикальні, а також ∠OBC=∠ODA і ∠OCB=∠OAD як внутрішні різносторонні при паралельних прямих BC, AD і січних AC, BD, відповідно. Звідси слідує, що трикутники ΔCOB і ΔAOD подібні, тому їх відповідні сторони (та інші відрізки, зокрема висоти) пропорційні, а площі відносяться як квадрати їх лінійних розмірів, див. формулу далі
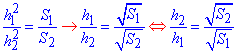
З площі трикутника ΔBOC виразимо меншу основу трапеції:
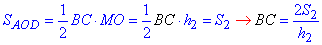
Аналогічним чином з площ ΔAOD виражаємо AD:
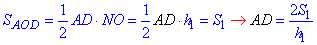
Виведемо площу трапеції через площі трикутників:
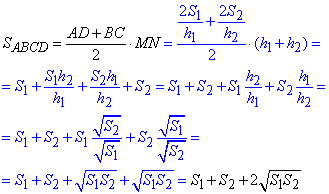
В отриману формулу підставляємо значення S1=4, S2=1
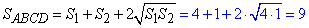
Відповідь: 9.
Попереду Вас чекають приклади на площу рвнобічних трапецій, а також на паралелограми, ромби, просторові фігури.


