Задачі на медіану, бісектрису, висоту та сторони трикутника

Далі будуть наведені задачі на знаходження відрізків, медіан, сторін трикутника. Прямого зв'язку між завданнями немає, однак аналіз їх розв'язків багато Вас навчить. Перш за все не боятися складних задач, навчить виконувати завдання на побудову, далі обчислення на основі властивостей трикутників.

Задача 39.27 У трикутнику ABC висота BK поділяє сторону AC на відрізки 1 і 3.

Знайти квадрат медіани BM трикутника ABC, якщо BK=2.
Розв'язання: Маємо трикутник ABC, у якого BK=2 - висота (BK⊥AC) і AC=4 (за умовою), причому AK=1 і CK=3.

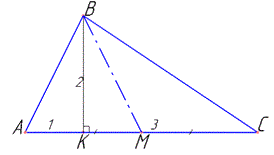
Проведемо медіану BM. Тоді AM=MC=AC:2=4:2=2, звідси
MK=AM-AK=2-1=1
Із прямокутного трикутника BKM (∠BKM=90) за теоремою Піфагора знайдемо квадрат гіпотенузи (медіани) BM:
.
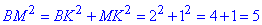Відповідь: 5.

Задача 39.39 Периметр трикутника дорівнює 50, а його бісектриса ділить протилежну сторону на відрізки завдовжки 15 і 5.
Знайти меншу сторону трикутника.
Розв'язання: Маємо трикутник ABC з периметром рівним 50. Побудуємо трикутник та позначимо сторони

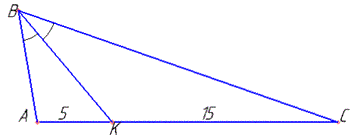
BK - бісектриса і AK=5, CK=15 (за умовою), звідси
AC=AK+CK=5+15=20

За властивістю бісектриси (бісектриса трикутника ділить протилежну сторону пропорційно бічним сторонам) позначимо:
AB=5x, BC=15x, де x - коефіцієнт пропорційності.
Звідси складаємо рівняння на периметр

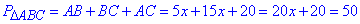
отримаємо
20x+20=50,
20x=30,
x=1,5.
Звідси AB=5•1,5=7,5 - менша сторона трикутника ABC.
Відповідь: 7,5

Задача 39.30 Сторона трикутника дорівнює 10.
Знайти квадрат довжини відрізка прямої, яка паралельна до цієї сторони та ділить площу трикутника навпіл.
Розв'язання: Маємо трикутник ABC зі стороною AC=10 (за умовою).

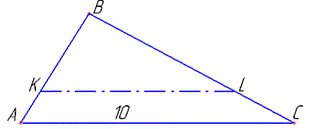
Його площу позначимо як S.
Проведемо відрізок CL паралельно до AC (KL||AC).
Тоді відрізок KL відтинає трикутник KBL, який є подібний до ΔABC (за властивістю), причому AC і KL - відповідні сторони цих трикутників.
Позначимо площу ΔKBL як S₁, причому S=2S₁ (за умовою).
Тоді за властивістю подібних трикутників, отримаємо
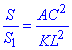, звідси

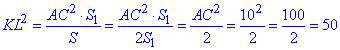
Відповідь: 50.

Задача 39.33 На сторонах AB і AC трикутника ABC відповідно позначено такі точки M і K, що ∠AMK=∠C, AM=4, MB=2 і AK=3.
Знайти довжину відрізка KC.
Розв'язання: Розглянемо трикутники AKM і ABC.

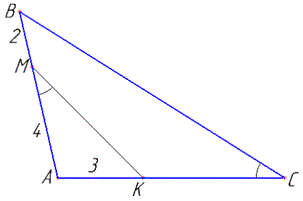
У них ∠A - спільний, ∠AMK=∠C (за умовою), звідси слідує, що ΔAKM і ΔABC подібні (за ознакою рівності двох відповідних кутів).
За умовою задачі маємо:
AB=AM+BM=4+2=6

Позначимо KC=x, тоді AC=AK+KC=3+x.
Отже, AK=3, AB=6 і AM=4, AC=3+x - відповідні сторони подібних трикутників.
Складемо відношення подібних сторін і знайдемо довжину відрізка KC:

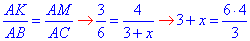
Звідси 3+x=8, KC=x=5.
Відповідь: 5

Задача39.35 Сторони трикутника дорівнюють 4 см, 5 см і 6 см.
Знайти з точністю до 0,01 см довжину медіани, проведеної до сторони завдовжки 5 см.
Розв'язання: Маємо трикутник ABC зі сторонами b=AB=4 см, a=AC=5 см і c=BC=6 см.

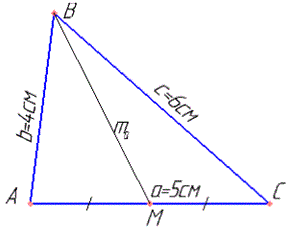
Для обчислення медіани m_a=BM використаємо формулу:

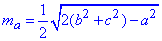
(Ця формула виводиться за допомогою теореми косинусів для трикутників ABC і ABM, у яких ∠A - спільний, а AC=2AM.
Її виведення тут не викладаємо).
Отже обчислимо довжину медіани m_a=BM, проведеної до сторони a=AC=5 см:
.
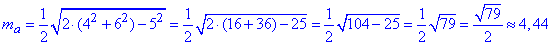Відповідь: 4,44

Задача 39.37 Дві сторони трикутника дорівнюють b і c, а бісектриса кута між ними дорівнює l.
Визначити третю сторону трикутника й обчислити її значення, якщо b=1, c=4, l=1,2.
Розв'язання: Нехай маємо трикутник ABC, у якого AB=b, AC=c і AK=l - бісектриса, звідси

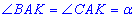
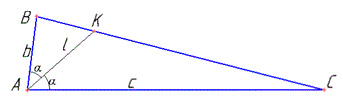
За властивістю бісектриси (бісектриса трикутника поділяє протилежну сторону пропорційно бічним сторонам) запишемо відношення:

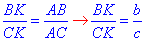
Позначимо: BK=bx і CK=cx, де x - коефіцієнт пропорційності.
Розглянемо трикутник ABK, у якого AB=b, AK=l і BK=bx, що лежить проти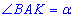
За теоремою косинусів запишемо рівність:
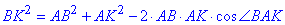, звідси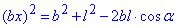
тоді 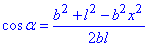. (1)
Розглянемо трикутник ACK, у якого AC=c, AK=l і CK=cx, що лежить проти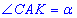
За теоремою косинусів запишемо рівність:
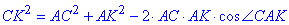, звідси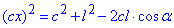
тоді 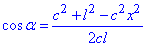. (2)
Прирівняємо отримані вирази (1) та (2) і знайдемо x:

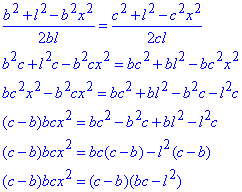
Оскільки
тобто 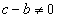за умовою, то ,
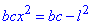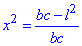, звідси .
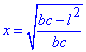Тоді .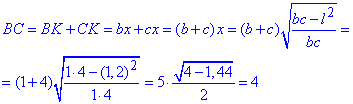
Отже, якщо у трикутника відомі дві сторони b, c і бісектриса l, то третя сторона a обчислюється за формулою:

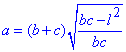
Відповідь: 4

Задача 39.38 У трикутнику, дві сторони якого дорівнюють a і b, сума висот, опущених на ці сторони дорівнює третій висоті.
Визначити третю сторону й обчислити її значення, якщо a=4, b=6.
Розв'язання: Нехай маємо трикутник ABC, у якого AB=a, AC=b.

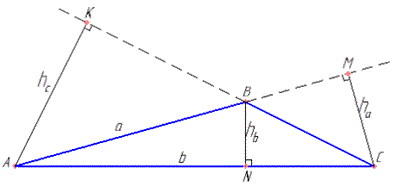
Позначимо: CM=h_a, BN=h_b і AK=h_C - висоти, що опущені до сторін AB, AC і BC відповідно, причому за умовою задачі:
h_C=h_a+h_b
позначимо третю сторону BC=c, яку треба знайти.
Запишемо вирази для обчислення площі S трикутника ABC:

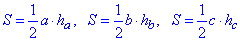
Прирівняємо попарно ці вирази і запишемо систему рівнянь, з якої знайдемо третю сторону c трикутника ABC:
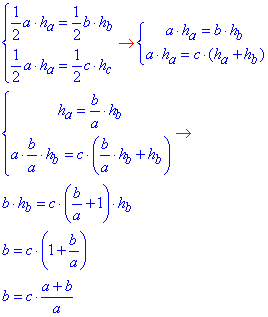
висота трикутика, система рівнянь
звідси отримаємо

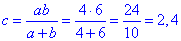
Відповідь: 2,4

З часом ми доповнимо цей розділ новими задачами, а поки що розбирайте наведені.
Вчіть властивості трикутнків, вивчайте формули, будуйте та досліджуйте трикутники. Без цьго Вам не освоїти геометрії.