На уроках з геометрії у 8 - 9 класах Вас чекає багатсько задач на площі геометричних фігур, серед яких частину займають трапеції. Попередньо були розв'язані задачі на середню лінію трапеції, знаходження висоти, довжини сторін і т.д.
Далі наведемо кілька цікавих задач на прямокутні трапеції і не тільки, а також детально розберемо методику обчислення такого класу завдань.
Задача 1. Знайдіть площу трапеції, основи якої дорівнюють 16 см і 30 см, а бічні сторони − 13 см і 15 см.
Розв'язування:Будуємо рисунок трапеції, позначаємо сторони, а далі за формулою Герона знаходимо площу трапеції.

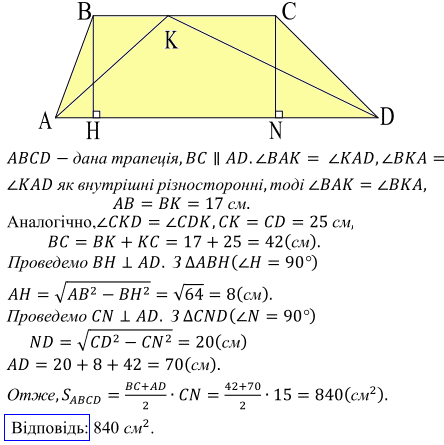
Задача 2. Точка перетину бісектрис гострих кутів при основі трапеції належить іншій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють 17 см і 25 см, а висота − 15 см.
Розв'язування:Тут важливо зауважити, що маємо не точки, а точка (однина). Тобто дві бісектриси перетинаються в одній точці. Наведемо рисунок до задачі і міркування, які допоможуть визначити сторони трапеції та знати площу.
Задача 3. Більша діагональ прямокутної трапеції ділить висоту, проведену з вершини тупого кута, на відрізки 15 см і 9 см, а бічна сторона дорівнює її меншій основі. Знайдіть площу трапеції.
Розв'язування:Побудуємо прямокутну трапецію за умовами задачі. та наведемо міркування для знаходження площі трапеції.
Уважно перегляньте як з пропорцій сторін трапеції знаходимо її площу.

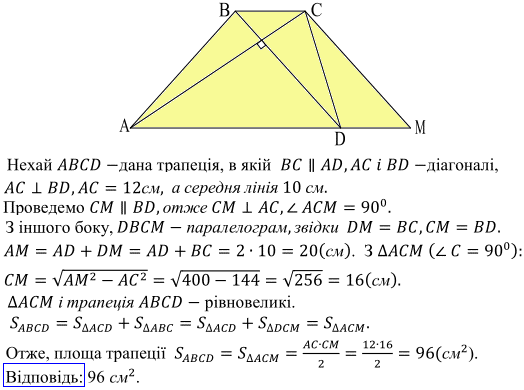
Задача 4. У трапеції ABCD діагоналі AC і BD перпендикулярні. Знайдіть площу цієї трапеції, якщо AC=12 см, а середня лінія трапеції дорівнює 10 см.
Розв'язування:Наведемо рисунок трапеції з перпендикулярними дагоналями.
Далі з певних закономірностей, що описані далі знайдемо сторони та площу трапеції.
Задача 5. Довжина кола, вписаного у прямокутну трапецію, дорвнює 24π см. Обчислити площу трапеції, якщо нижня її основа на 10 см довша за її верхню основу.
Розв'язування:Побудуємо трапецію за умовою. Легко здогадатися, що діаметр кола рівний висоті трапеції. Решта міркувань для обчислення площі прямокутної трапеції наведено нижче.

Якщо хочете допомогти в розвитку сайту то просимо надсилати цікаві задачі та, в такий спосіб, покращувати наявну бібліотеку готових задач!


