Якщо Ви тільки знаєте, що рівнобічна трапеція – це трапеція у якої рівні бічні сторони, то Ви практично нічого не знаєте. В рівнобічної трапеції рівні діагоналі, кути при основах також рівні. Це дозволяє отримати набагато більше формул, ніж для різносторонніх трапецій.
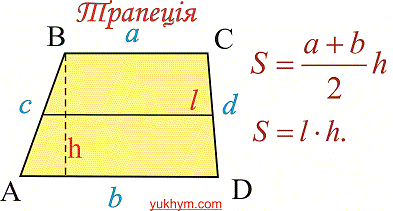
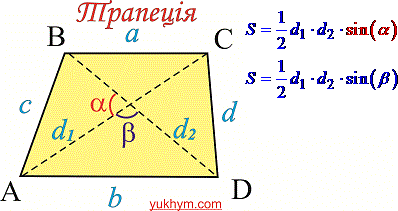
Протилежні кути в рівнобічних трапеціях є суміжними, отже кожна така трапеція є вписаним чотирикутником, тобто навколо рівнобчних трапецій можна описати коло. Так само можна і вписати коло. Якщо в завданні відомо, що в рівнобічну трапецію вписано коло (бічні сторони рівні) то одночасно з основними формулами площі трапеції використовують наступні:
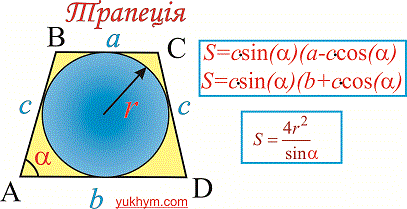
Коло вписане (описане) в рівнобічну трапецію
Приклад 32.18 У рівнобічну трапецію вписане коло. Знайти квадратних сантиметрах площу трапеції, якщо її основи дорівнюють 2 см і 8 см.
Обчислення: Нехай маємо рівнобічну трапецію ABCD, AD||BC, BC=2 см, AD=8 см, AB=CD, BH⊥AD, де BH– висота трапеції, опущена на сторону AD.
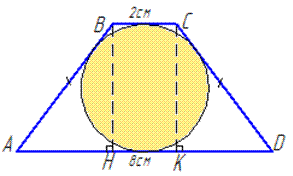
Оскільки у рівнобічну трапецію ABCD вписане коло, то суми її протилежних сторін рівні (за властивістю чотирикутника, описаного навколо кола), тобто AB+CD=AD+BC, звідси
2AB=8+2=10, AB=AD=10/2=5 см.
Опустимо ще одну висоту CK на сторону AD, тобто CK⊥AD (∠CKD=90).
Розглянемо прямокутні трикутники ABH і KCD.
У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=5 см.
Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), і, отже, AH=KD=(8-2)/2=3 см.
У прямокутному трикутнику ABH (∠AHB=90) знайдемо катет BH за теоремою Піфагора:
AB^2=AH^2+BH^2, звідси
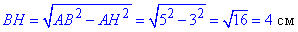
Отже, BH=CK=4 см – висота рівнобічної трапеції ABCD.
Звідси тепер неважко довести теорему:
висота рівнобедреної трапеції, в яку можна вписати коло, є середнім геометричним її основ, тобто
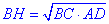
Знайдемо площу трапеції:
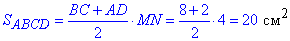
Відповідь: 20 см2 – В.
Приклад 32.38а У рівнобічну трапецію, верхня основа якої удвічі менша від її висоти, вписане коло, радіус якого дорівнює 3 см. Знайти у квадратних сантиметрах площу трапеції.
Розв'язування: Нехай задано рівнобічну трапецію ABCD (AD||BC), у якої вписане коло з центром у точці O та радіусом r=3 см (за умовою); AD||BC – основи та AB=CD – бічні сторони. Діаметр вписаного кола: d=2r=2•3=6 (см). Наведемо рисунок трапеції з вписаним у неї колом
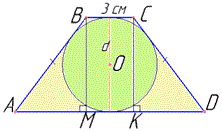
З вершин B і C до основи AD проведемо висоти трапеції BM і CK, відповідно: BM⊥AD і CK⊥AD (очевидно, що BM=CK). Оскільки вписане коло дотикається до основ AD і BC (в точці дотику вписаного кола радіус перпендикулярний до дотичних сторін), то діаметр вписаного кола дорівнює висоті трапеції ABCD, отже BM=CK=d=6 см. Звідси слідує, що BC=BM:2=6:2=3 (см) за умовою.
Позначимо: AB=CD=x. Тоді у прямокутному трикутнику ABM (∠M=90) за теоремою Піфагора запишемо вираз для знаходження катета AM: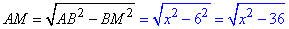 
Оскільки трапеція ABCD рівнобічна, то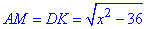 
і MK=BC=3 см. Тоді
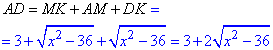
За властивістю вписаного кола в чотирикутник (якщо у чотирикутник вписано коло, то суми його протилежних сторін рівні) запишемо рівність для знаходження x:
AB+CD=BC+AD,
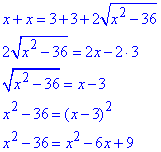
6x=45, звідси x=7,5. Отже, маємо AB=CD=7,5 см і AD
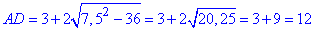(см).
Знайдемо площу рівнобічної трапеції:
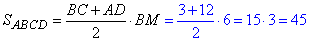(см2).
Відповідь: 45.
Приклад 32.40а Навколо трапеції описане коло, діаметром якого є більша основа. Обчислити площу трапеції у квадратних сантиметрах, якщо її діагональ і висота відповідно дорівнюють 5 см і 3 см.
Розв'язування: Нехай маємо рівнобічну трапецію ABCD (AD||BC), навколо якої описане коло з центром у точці O, причому AO=DO (AD - діаметр кола за умовою); AC=5 см - діагональ і CK=3 см - висота, що проведена до основи AD (CK⊥AD). Наведемо схематичний рисунок до задачі
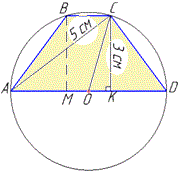
За теоремою Піфагора знайдемо катет AK у прямокутному трикутнику ΔACK (∠K=90):
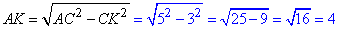(см).
Позначимо: AO=DO=x, тоді KO=4-x.
Відрізок CO сполучає центр кола O з точкою C на колі, тому цей відрізок є радіусом описаного кола, звідси CO=x.
У прямокутному трикутнику ΔCOK (∠K=90) запишемо формулу Піфагора і знайдемо невідому x:
CO^2=CK^2+KO^2,
x^2=3^2+(4-x)^2,
x^2=9+16-8x+x^2,
8x=25, звідси x=25/8=3,125.
Отже, AO=DO=25/8 см, тоді AD=2•AO=2•25/8=25/4 см.
Лише рівнобічна трапеція може бути вписана у коло (за властивістю), тому
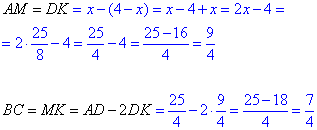
Маємо обчисленими AD=25/4 см і BC=7/4 см – основи трапеції ABCD.
Можемо знайти площу трапеції через добуток півсуми основ на її висоту:
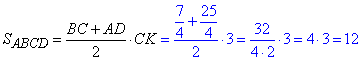(см2).
Відповідь: 12.
Задача 1. Коло, вписане в рівнобічну трапецію, ділить точкою дотику бічну сторону на відрізки 8 см і 18 см. Знайдіть площу трапеції.
Розв'язування:Коло тут будувати не будемо, лише трапецію. Відрізок, що з'єднує центр вписаного кола з точкою дотику OM є перпендикулярним до сторони трапеції.
Друга важлива пдказка в таких задачах, що кут COM є прямим, звідси випливає що висота прямокутного трикутника OM рівна кореню квадратному з добутку довжин відрізків на які висота ділить основу CD.
Решта обчислень приведено нижче:
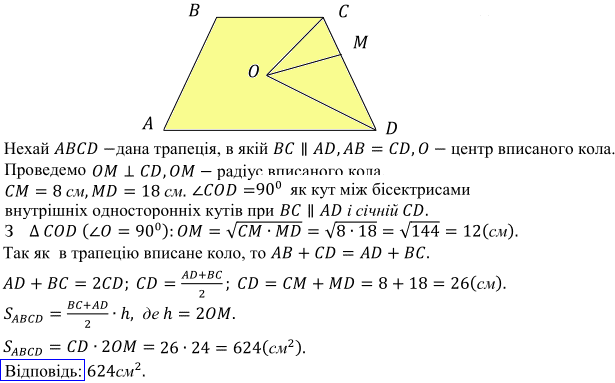
Площа рівнобічної трапеції. ЗНО тести
Приклад 32.40 Діагональ рівнобічної трапеції є бісектрисою її гострого кута і ділить середню лінію трапеції на відрізки довжиною 13 см і 23 см. Обчислити (у см2) площу трапеції.
Розв'язування: Нехай маємо рівнобічну трапецію ABCD;
AD||BC - основи та AB=CD – бічні сторони. Діагональ AC є бісектрисою гострого ∠A (за умовою), тому ∠BAC=∠CAD і перетинає середню лінію MN в точці O, причому MO=13 см і NO=23 см, звідси MN=MO+NO=13+23=36 см.
∠BCA=∠CAD як внутрішні різносторонні кути при паралельних прямих AD, BC та січній AC. Звідси слідує, що ∠BCA=∠BAC, тому ΔABC рівнобедрений з основою AC і бічними сторонами AB=BC.
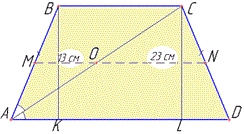
У триктнику ΔABC відрізки MO||BC паралельні і AM=BM рівні (як частина відрізка MN), тому відрізок MO – середня лінія трикутника ΔABC, звідси BC=2•BC=2•13=26 (см). Тоді CD=AB=BC=26 см.
У трикутнику ΔACD відрізок NO||AD і CN=DN (як частина відрізка MN), тому відрізок NO – середня лінія ΔACD, звідси AD=2•NO=2•23=46 (см).
Оскільки трапеція ABCD рівнобічна, то маємо KL=BC=26 см і AK=DL=(46-26):2=10 (см), де BK і CL – висоти, що проведені до основи AD.
У прямокутному ΔABK (∠K=90) за теоремою Піфагора знайдемо катет BK - висоту рівнобічної трапеції ABCD:
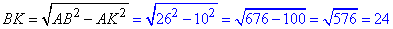(см).
Знайдемо площу трапеції ABCD:
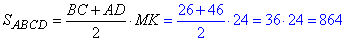(см2).
Відповідь: 864.
Приклад 32.46 Канал з Дніпра до Кривого Рогу в районі села Червоні Поди має у поперечному перерізі форму рівнобедреної трапеції, у якої довжина більшої основи дорівнює 12 м, висота 3 м, а бічні сторони нахилені до основи під кутом 450. Швидкість руху води в каналі дорівнює 3 м/хв. Скільки кубічних метрів води забирається з Дніпра за 1 хв?
Розв'язування: Зробимо математичну модель задачі. Поперечний переріз каналу замінимо на рівнобічну трапецію ABCD (BC||AD), у якої AB=CD – бічні сторони, AD=12 м– довжина більшої основи, BK=CM=3 м – висота (BK⊥AD, CM⊥AD), ∠BAD=45 – кут нахилу бічних сторін до основи AD (за умовою).
Схематичний вигляд перевернутого каналу наведено далі
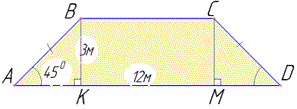
Кількість води, яка забирається з Дніпра з певною швидкістю v і за певний проміжок часу t дорівнює об'єму цієї води V, що пройшла шлях h зі швидкістю v і за час t, тобто
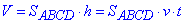
де SABCD – площа трапеції ABCD;
v=3 м/хв – швидкість руху води; t=1 хв - час.
Розглянемо прямокутний ΔABK (∠K=90), у якого BK=3 м – протилежний катет до кута ∠BAK=45. Із теореми про суму кутів трикутника випливає, що ∠ABK=∠ABK=45. Отже, трикутник ΔABK– рівнобедрений з бічними сторонами BK=AK=3 м.
Оскільки трапеції ABCD рівнобедрена за умовою, то трикутники рівні ΔABK=ΔDCM (а отже їх відповідні сторони рівні), тому DM=AK=3 м.
Обчислимо довжину меншої основи BC:
BC=KM=AD-2AK=12-2•3=6 (м).
Знайдемо площу рівнобічної трапеції:
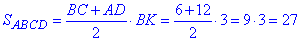
Порахуємо кількість води (об'єм V), що забирається з Дніпра за час t=1 хв:
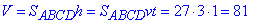
Відповідь: 81.
Задача 2. Основи рівнобічної трапеції дорівнюють 12 і 18 см, а діагональ є бісектрисою її гострого кута. Обчисліть площу цієї трапеції.
Розв'язування: Побудуємо трапецію за умовами задачі
У вас можуть бути інші розміри, головне запам'ятати як обчислювати коли в умові вказано, що діагональ є одночасно бісектрисою кута в трапеції.
Задача 3. Знайдіть площу рівнобічної трапеції, основи якої дорівнюють 5 см і 13 см, а діагоналі перпендикулярні до бічних сторін.
Розв'язування:Побудуємо трапецію за умовами задачі та наведемо міркування для знаходження площі трапеції.
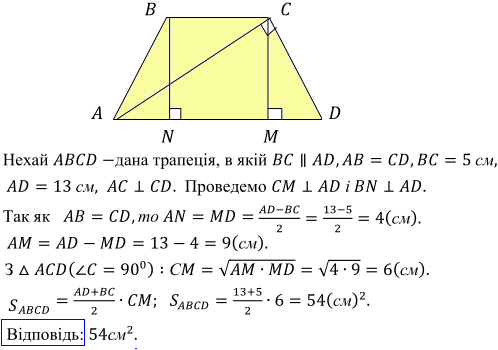
Більше готових відповідей з геометрії на трапецію, ромб, паралелограм Ви можете знайти на сусідніх сторінках сайту.
