В шкільному курсі геометрії серед основних задач значну увагу приділено прикладам обчислення площі та периметру ромба. Пригадаємо, що ромб належить до окремого класу чотирикутників і вирізняється серед них рівними сторонами. Ромб також є частковим випадком паралелограма, якщо в останнього всі сторони рівні AB=BC=CD=AD. Нижче зображено рисунок, на якому зображено ромб і наведені основні формули для обчислення площі та периметру ромба.
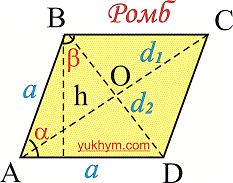
Властивості ромба
Оскільки ромб займає деяку частину паралелограмів, то властивості в них будуть схожими.
- Протилежні кути ромба як і паралелограма рівні.
- Сума кутів ромба, які прилягають до однієї сторони рівна 180°.
- Діагоналі ромба перетинаються під кутом 90 градусів.
- Діагоналі ромба є одночасно бісектрисами його кутів.
- Діагоналі ромба в точці перетину діляться пополам.
Ознаки ромба
Усі ознаки ромба випливають із його властивостей і допомагають розрізняти його серед чотирикутників, прямокутників, паралелограмів.
- Паралелограм у якого діагоналі перетинаються під прямим кутом є ромбом.
- Паралелограм у якого діагоналі є бісектрисами є ромбом.
- Паралелограм із рівними сторонами є ромбом.
- Чотирикутник у якого всі сторони рівні є ромбом.
- Чотирикутник у якого діагоналі є бісектрисами кутів і перетинаються під прямим кутом є ромбом.
- Паралелограм з однаковими висотами є ромбом.
Формула площі ромба
Формул для обчислення площі наведені на рисунку.
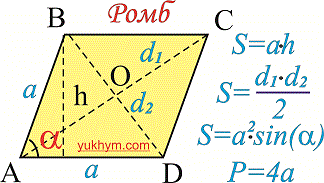
Найпростіша виводиться як сума площ двох трикутників, на які ділить ромб його діагональ.
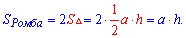
Друга формула площі застосовується до задач, в яких відомі діагоналі ромба. Тоді Площа ромба рівна половині добутку діагоналей
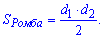
Досить проста для того, щоб запам'ятати, а також для обчислень.
Третя формула площі має зміст коли відомий кут між сторонами. Згідно неї площа ромба рівна добутку квадрату сторони на синус кута. Гострий він чи ні значення не має, оскільки синус обох кутів приймає однакове значення.
Формула периметру ромба
Периметр за означенням рівний сумі усіх сторін. Оскільки в ромба всі сторони рівні то його периметр обчислюємо за формулою
P=4a.
Периметр вимірюєтья в одиницях довжини.
Радіус кола вписаного в ромб
Одними з поширених завдань при вивченні ромба є знаходження радіуса чи діаметра вписаного кола. На рисунку зображеному нижче наведено одні з поширених формул радіуса вписаного кола в ромб.

Перша формула показує, що радіус кола вписаного у ромб рівний добутку діагоналей розділеному на суму всіх сторін (4а).
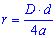
Інша формула показує, що радіус кола вписаного у ромб рівний половині висоти ромба
r=h/2.
Друга формула на рисунку є модифікацією першої і застосовується при обчисленні радіусу кола вписаного у ромб коли відомо діагоналі ромба, тобто невідомі сторони.
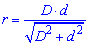
Третя формула радіусу вписаного кола фактично знаходить половину висоти малого трикутника, який утворюється перетином діагоналей.
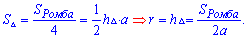
Серед менш популярних формул для обчислення радіуса кола вписаного у ромб можна ще привести такі
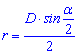
тут D– діагональ ромба, alpha– кут, з якого виходить діагональ.
Якщо відома площа (S) ромба та величина гострого кута (alpha), то для обчислення радіуса вписаного кола потрібно знайти квадратний корінь з четвертин добутку площі на синус гострого кута:
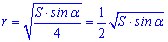
З наведених формул Ви без проблем знайдете радіус кола вписаного у ромб, якщо в умовах прикладу будуть необхідний набір даних.
Периметр ромба
Периметр ромба рівний сумі всіх його сторін. Зважаючи на те, що вони усі рівні периметр приймає значення
P=4a.
І на завершення запам'ятайте, що периметр вимірюється в одиницях дожини, а площа в квадратних одиницях. Тепер Ви знаєте як знайти площу та периметр ромба, тож користуйтеся наведеними формулами при розв'язуванні задач.


