Ромб. Обчислення площі, висоти, діагоналей

Сьогодні розглянемо розв'язки задач на площу ромба, знаходження висоти та діагоналей. Для обчислення прикладів потрібно знати властивості ромба та вміти їх застосовувати на практиці.
За кілька уроків на 29 прикладах Ви зможете оновити в пам'яті знання з шкільного курсу геометрії за 8-10 класи.
Готові відповіді до задач на ромб допоможуть при підготовці до ЗНО тестів з математики, а також школярам, що вивчають дану тему.

Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Завантажити онлайн відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).

Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.

Тема 32. Чотирикутники

Задачі на ромб

Приклад 32.7 Діагональ ромба утворює з однією зі сторін кут, що дорівнює 54 градуси. Знайти менший кут ромба.

Обчислення: Вводимо прості позначення, характерні для ромба ABCD, O – точка перетину діагоналей AC і BD, ∠ACB=54 – кут між діагоналлю AC і стороною BC у ромбі ABCD.

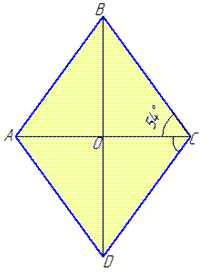
За властивістю: діагоналі ромба є бісектрисою його кутів, маємо
∠ACB=54, тому ∠C=54+54=108.
Оскільки кожен ромб – це паралелограм, то протилежні кути ромба рівні, а сума сусідніх кутів дорівнює 180⁰.
Тому ∠A=∠C=108, ∠B+∠C=180, звідси
∠B=180-∠C=180-108=72.
Отже, ∠A=∠B=72– менший кут ромба.
Відповідь: 72⁰ – В.

Приклад 32.8 Одна з діагоналей ромба дорівнює 30 см. Знайти іншу діагональ ромба, якщо його периметр дорівнює 68 см.

Обчислення: Нехай маємо ромб ABCD, AC і BD=30 см – діагоналі ромба,
P_ABCD=68 см – периметр ромба.

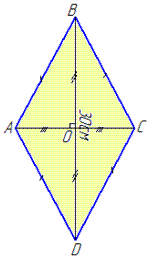
Оскільки ромб – це паралелограм, у якого всі сторони рівні, то

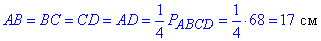
За властивістю паралелограма (діагоналі в точці перетину діляться навпіл):
BO=OD=30/2=15 см, а також AO=OC.
За властивістю ромба (діагоналі перетинаються під прямим кутом) маємо AC⊥BD, тому AO⊥OB, тобто ∠AOB=90.
У прямокутному трикутнику AOB (∠AOB=90) відомо:
BO=15 см – катет, AB=17 см – гіпотенуза.
За теоремою Піфагора знайдемо катет AO:
AB^2=AO^2+OB^2, звідси

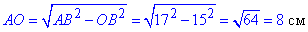
Звідси, AC=2AO=2•8=16 см – друга діагональ ромба.
Відповідь: 16 см - Г.

Приклад 32.9 Сторона ромба дорівнює 6 см, а його площа – 18 см2. Знайти найбільший кут ромба.

Обчислення: Нехай маємо ромб зі стороною a=6 см (у нього всі сторони рівні), площею S=18 см².

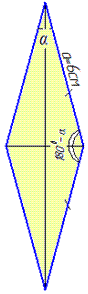
Площа ромба (як і будь-якого паралелограма) обчислюється за формулою:
S=a^2•sin(alpha), де alpha – кут між сторонами ромба.
Отже, 18=6^2• sin(alpha), звідси sin(alpha)=18/36=1/2.
Оскільки 0< alpha <180, то alpha[1]=30 і alpha[2]=180-30=150, так як sin(alpha)= sin(180-alpha).
Звідси, alpha=150 – найбільший кут ромба.
Відповідь: 150⁰ - Д.

ЗНО 2019. Завдання 26. На рисунку зображено ромб ABCD, діагоналі якого перетинаються в точці O. Із цієї точки до сторони AD проведено перпендикуляр OK довжиною 3 см. Площа трикутника AOD дорівнює 15 см².

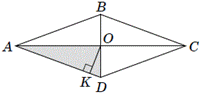
1. Визначте довжину сторони ромба ABCD (у см).
2. Обчисліть тангенс гострого кута ромба ABCD.
Розв'язування: 1. Розглянемо трикутник AOD, у якого OK=3 см - висота, OK⊥AD і S_ΔAOD=15 см₂.
Знайдемо сторону AD ромба через площу трикутника:

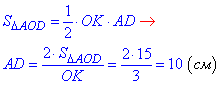
AD=AB=BC+CD=10 см - довжина сторони.

2. Площа ромба ABCD через кут:

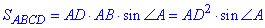
де ∠A - гострий кут. З іншої сторони,
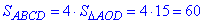(см²),
тому що діагоналі перетинаються під прямим кутом, є бісектрисами кутів ромба і розділяють ромб на 4 рівних прямокутних трикутників.
З врахуванням рівності сторін, розписуємо площу

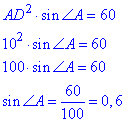
Обчислимо косинус гострого кута ромба
(тут sin∠A>0 і cos∠A>0 ):
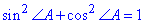- основна тригонометрична тотожність,
звідси

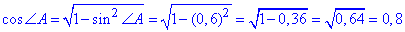
Знайдемо тангенс гострого кута ромба

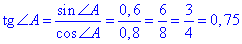
Відповідь: 10; 0,75.

Приклад 32.21 У ромбі ABCD більша діагональ AC поділяє висоту BK на відрізки BM=5 см і MK=3 см.
Знайти площу ромба.

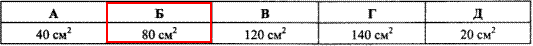
Обчислення: Нехай маємо ромб ABCD, BM=5 см і MK=3см, BK=BM+MK=5+3=8 см, де BK– висота ромба, опущена на сторону AD (BK⊥AD), AC– діагональ ромба.

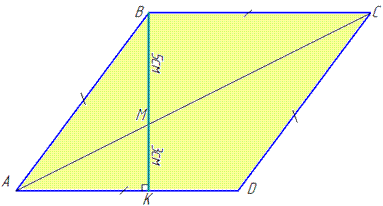
Розглянемо прямокутні трикутники AKM (∠AKM=90) і CBM (∠CBM=90).
∠AMK=∠CMB (як вертикальні), ∠MAK=∠MCB (як внутрішні різносторонні кути при перетині січною AC паралельних прямих AD і BC).
Звідси слідує, що ΔAKM~ΔCBM (подібні за трьома кутами) і тому їх сторони подібні.
Отже, AK=3k і BC=5k, де k – коефіцієнт пропорційності.
Оскільки, за означенням, у ромба всі сторони рівні, то AB=BC=CD=AD=5k.
Розглянемо прямокутний трикутник AKB (∠AKB=90), у якого BK=8 см, AK=3k – катети, AB=5k – гіпотенуза.
За теоремою Піфагора запишемо рівність:

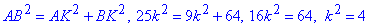
звідси k=2. Отже, AD=5•2=10 см.
Знайдемо площу ромба:
S=BK•AD=8•10=80 см².
Відповідь: 80 см^2 – Б.

Приклад 32.26 Діагональ ромба утворює зі стороною кут 60⁰.
Установити відповідність між довжинами сторін (1–4) ромба і площами (А–Д) прямокутників з вершинами на серединах сторін ромба.

Обчислення: Нехай маємо ромб ABCD, AB=BC=CD=AD=a см – сторони ромба (за означенням сторони ромба рівні).
KLMN – прямокутник з вершинами на серединах сторін ромба ABCD.

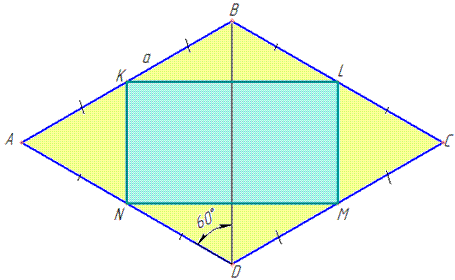
Оскільки сторони ромба рівні, то ΔABD – рівнобедрений, тому ∠ADB=∠ABD=60.
Із суми кутів трикутника слідує, що ∠BAD=60.
Отже, ΔABD – рівносторонній, звідси BD=a см.
Так як відрізок KN з'єднує середини сторін AB і Ad відповідно, то KN – середня лінія ΔABD, тому KN=LM=a/2 см.
У прямокутному трикутнику NPD (∠NPD=90) маємо:
ND=a/2 і ∠NDP=60.
За означенням синуса гострого кута знайдемо катет NP:

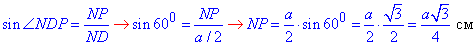
Маємо 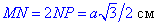(оскільки діагональ BD ділить MN відрізок навпіл).
Отже, KN=a/2 см – ширина і 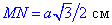– довжина прямокутника KLMN.
Площа прямокутника KLMN:

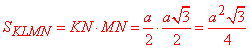
На основі формули знаходимо площі ромбів та записуємо у відповіді:

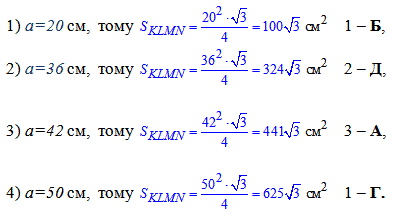
Приклад 32.25 Установити відповідність між фігурами (1–4) та їхніми характерними властивостями (А–Д).
1. Описаний навколо кола чотирикутник
2. Вписаний у коло чотирикутник
3. Паралелограм
4. Ромб

А. Сума протилежних кутів дорівнює 180⁰.
Б. Діагоналі рівні.
В. Суми протилежних сторін рівні.
Г. Сума кутів при одній стороні дорівнює 180⁰.
Д. Діагоналі є бісектрисами кутів.
Обчислення: Дані висновки ґрунтуються виключно на властивостях чотирикутників і вимагають детальних пояснень.
Для себе запам'ятайте наступні відповіді, вони перевірені та правильні.
1 – В, 2 – А, 3 – Г, 4 – Д.

Приклад 32.34 Діагоналі ромба відносяться як 3:4. Знайти висоту ромба, якщо його периметр дорівнює 80.
Розв'язування: Нехай маємо ромб ABCD, у якого P_ABCD=80, BD:AC=3:4 (за умовою), де BD і AC – діагоналі ромба, які перетинаються в точці O. Оскльки всі сторони ромба рівні, то AB=BC=CD=AD=PABCD:4=80:4=20 - довжина сторони ромба ABCD. Побудуємо схематичний рисунок ромба

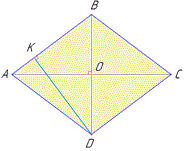
Позначимо BD=3x, тоді AC=4x, де x - коефіцієнт пропорційності з умови.
За властивістю діагоналей ромба маємо:
BO=OD=BD:2=1,5x, AO=OC=AC:2=2x і AC⊥BD.
У прямокутному трикутнику ΔAOB (∠O=90) за допомогою теореми Піфагора складемо рівняння для знаходження невідомої x:
AO^2+BO^2=AB^2,
(2x)^2+(1,5x)^2=20^2,
4x^2+2,25x^2=20^2,
6,25x^2=20^2,
(2,5x)^2=20^2,
2,5x=20,
x=8.
Обчислюємо BD=3•8=24 та AC=4•8=32 - довжини діагоналей ромба.
Запишемо формули для обчислення площі ромба:
S_ABCD=AC•BD, з іншої сторони S_ABCD=AB•DK, де DK - висота ромба, що проведена до сторони AB. Прирівнявши одну площу до іншої можемо виразити шукану висоту ромба

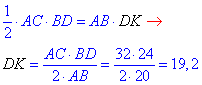
Відповідь: 19,2.

Приклад 32.35 Сума довжин діагоналей ромба дорівнює l, а площа ромба – S. Визначити сторону ромба й обчислити її значення, якщо l=14, S=24.
Розв'язування: Нехай задано ромб ABCD, у якого SABCD=S, BD+AC=l (за умовою), де BD, AC – діагоналі ромба, які перетинаються в точці O. Наведемо рисунок ромба до задачі

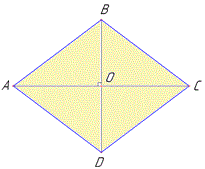
За властивістю діагоналей ромба маємо:
BO=OD=BD:2, AO=OC=AC:2 та AC⊥BD.
Для прямокутного трикутника ΔAOB (∠O=90) за теоремою Піфагора запишемо
AO^2+BO^2=AB^2.
Формула для обчислення площі ромба ABCD:

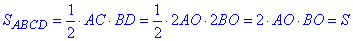
звідси 2•AO•BO=S.
Подвійний добуток нам потрібний в наступних обчисленнях.
За допомогою алгебраїчних перетворень знайдемо довжину сторони ромба:
l=AC+BD=2•AO+2•BO=2•(AO+BO)

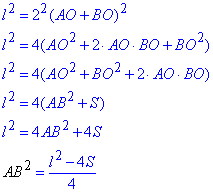
Вивели формулу для знаходження сторони ромба через суму діагоналей та площу ромба
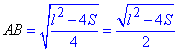- формула довжини сторони ромба.
Виконуємо підстановку значень з умови: l=14, S=24

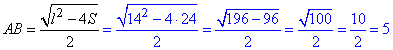
Відповідь: 5.

Приклад 32.44 Висота ромба дорівнює 24, а менша діагональ – 30. Знайти більшу діагональ ромба.
Розв'язування: Наведемо схематичний рисунок ромба ABCD, у якого AC=30 - менша діагональ, AK=24 - висота (за умовою), AK⊥BC.

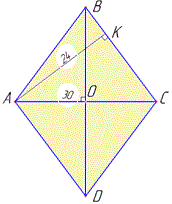
BD і AC – діагоналі ромба, які перетинаються в точці O.
За властивістю діагоналей ромба маємо:
BO=OD=BD:2, AO=OC=AC:2=30:2=15 і AC⊥BD.
Запишемо формули для обчислення площі ромба:

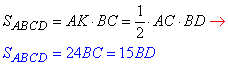
Позначимо: a - сторона і d - менша діагональ ромба.
Тоді отримаємо 24a=15d, звідси a=5d/8.
Маємо також: BO=BD/2=d/2 і AB=BC=a.
За теоремою Піфагора для прямокутного трикутника ΔAOB (∠O=90) складемо рівняння відносно d
AO^2+BO^2=AB^2,

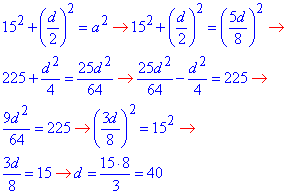
BD=d=40 - менша діагональ ромба ABCD.
Відповідь: 40.