Многокутники. Формули та приклади

Формули правильних многокутників

Многокутник - n-кутник зі стороною a_n .
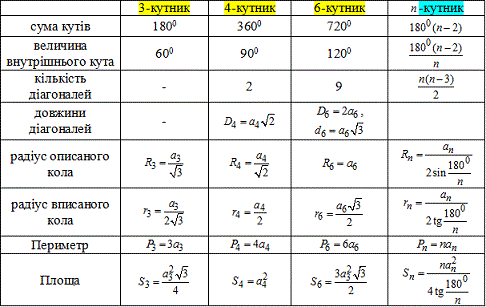
В таблиці виписані формули площі, периметра, радіусів вписаного та описаного кіл, кількості та довжини діагоналей, кути для трикутника, чотирикутника, шестикутника, та n-кутника.

Деякі інші співвідношення у правильному многокутнику (n-кутнику):

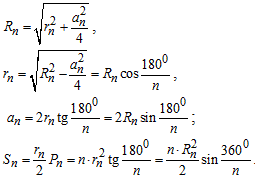
R – радіус описаного кола, радіус многокутника,
r – радіус вписаного кола, апофема многокутника.
Наведені формули краще видрукувати та мати під рукою, коли самостійно будете розв'язувати задачі на многокутники.

Властивості многокутника

А) Довжина ламаної не менша за довжину відрізка, що сполучає її кінці.
Б) Сума кутів опуклого n- кутника дорівнює 180⁰(n-2).
В) Сума зовнішніх кутів опуклого n- кутника, узятих по одному при кожній вершині, дорівнює 360⁰.
В) Правильний опуклий многокутник є вписаним у коло і описаним навколо кола. Центри вписаного та описаного кола збігаються.
Г) Правильні n- кутники подібні. Зокрема, якщо у них сторони однакові, то вони рівні.

ЗНО тести

Проаналізуємо розв'язки понад 30 завдань із ЗНО тестів, які навчать Вас застосовувати наведені вище формули многокутників на практиці.

Приклад 33.1 Скільки всього діагоналей має десятикутник?

Розв'язування: Діагональ многокутника – відрізок, що сполучає дві несусідні його вершини.
Для кращого розуміння Що задано? та Що потрібно знайти? в геометричних задачах виконуйте побудову. Простий рисунок не забере у Вас багато часу, проте внесе ясність, що від Вас хочуть.
Побудуємо десятикутник та діагоналі з однієї вершини.

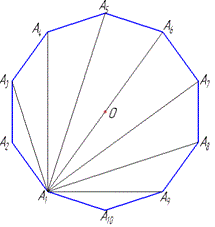
З кожної вершини n-кутника можна провести (n-3) діагоналі, переконайтеся в цьому твердженні з рисунка.
Всього маємо  n вершин, причому слід зауважити, що кожну діагональ при обході записуємо двічі, наприклад, А₁А₁₀ і А₁₀А₁. 
Це теж логічно і Ви повинні розуміти чому так?
Тому формула для обчислення кількості діагоналей многокутника (n-кутника):
n(n-3)/2,
де n - кількість вершин.
Для десятикутника (n=10) маємо:
10•(10-3)/3=5•7=35.
Відповідь: 35 – Д.

Приклад 33.2 Чому дорівнює сума внутрішніх кутів опуклого дванадцятикутника?

Розв'язування: Формула для обчислення суми внутрішніх кутів опуклого многокутника (n-кутника):
180⁰(n-2), де n - кількість вершин многокутника.

Для дванадцятикутника (n=12) маємо:
180⁰(12-2)=180⁰•10=1800⁰.

Дане завдання можна розв'язати чисто з логічних міркувань, навіть при цьому вивести формулу, що сума внутрішніх кутів опуклого многокутника рівна 180⁰(n-2).
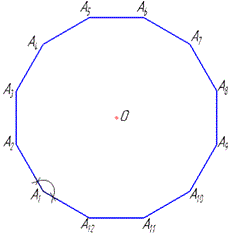
В наведеному вище дванадцятикутнику побудуємо діагоналі з однієї точки.
Отримаємо (n-2) трикутників, що у нашому випадку рівно 10.

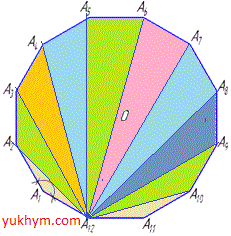 Розфарбуймо та переконайтеся, що саме стільки трикутників дістанемо.
Далі з геометрії за 7-8 класи Ви повинні знати, що сума внутрішніх кутів трикутника рівна 180 градусів.
Помноживши кількість трикутників на 180 градусів дістанемо суму внутрішніх кутів опуклого дванадцятикутника
10•180⁰=1800⁰
Використовуйте логічне мислення всюди де це можливо, оскільки всі формули тримати в голові нереально.
А логіка, повірте, виручає частіше ніж знання шкільного матеріалу.
Відповідь: 1800⁰ – А.

Приклад 33.3 Скільки вершин має опуклий многокутник, якщо сума його внутрішніх кутів дорівнює 900⁰?

Розв'язування: Використаємо формулу для обчислення суми внутрішніх кутів опуклого многокутника:

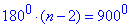
n-2=5, звідси n=7.
Рисунок правильного семикутника наведено нижче

Відповідь: сім – В.

Приклад 33.4 Якщо в опуклому многокутнику всі кути гострі, то він…

Розв'язування: Формула для обчислення внутрішнього кута правильного опуклого многокутника (n-кутника):
180⁰(n-2)/n, де n - кількість вершин многокутника.
За умовою задачі сказано, що всі кути опуклого многокутника гострі, тобто менше за 90⁰.
Складаємо залежність

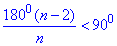
Розв'яжемо отриману нерівність:
враховуючи, що n - натуральне число (означає кількість), то

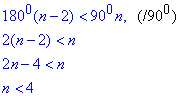
звідси n< 4, тобто n=3.

Отримали важливий висновок:
якщо в опуклому многокутнику всі кути гострі, таким многокутником може бути тільки трикутник!
Відповідь: трикутник – А.

Приклад 33.5 Чому дорівнює внутрішній кут правильного восьмикутника?

Розв'язування: Використаємо формулу для обчислення внутрішнього кута опуклого многокутника, n=8:

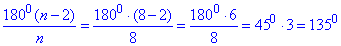
Наведемо рисунок восьмикутника
 Відповідь: 335⁰ – Г.

Приклад 33.6 Скільки сторін має правильний многокутник, якщо його внутрішній кут дорівнює 156⁰?

Розв'язування: Повторимо формулу для обчислення внутрішнього кута опуклого правильного многокутника (n-кутника):

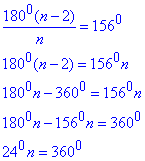
звідси n=15 сторін.
Відповідь: 15 – В.

Приклад 33.7 Скільки вершин має правильний многокутник, якщо його зовнішній кут дорівнює 20 градусів?

Розв'язування: Зовнішній і внутрішній кут опуклого многокутника є суміжними кутами, тому обчислимо внутрішній кут заданого многокутника:
180⁰-20⁰=160⁰.
Використаємо формулу для обчислення внутрішнього кута опуклого правильного многокутника (n-кутника):

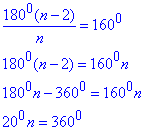
звідси n=18 вершин.
Відповідь: 18 – Г.

Приклад 33.8 Якщо у правильного многокутника всі діагоналі рівні, то він...

Розв'язування: Лише у правильних чотирикутників і п'ятикутників кожна діагональ розділяє цю фігури на дві інших, одна з яких є трикутник.

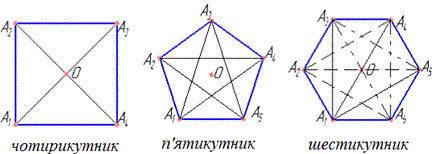
 Утворені трикутники є рівними за двома сторонами і кутом між ними (у правильних многокутників всі сторони рівні і всі кути також рівні). Тому всі діагоналі правильних чотирикутників і п'ятикутників рівні.
У шестикутника діагоналі A1A4, A2A5, A3A6 розділяють його на дві рівних (рівнобічних) трапеції, а діагоналі A1A3, A1A5, A2A6 і т.д. розділяють правильний шестикутник на трикутник і п'ятикутник.
Оскільки трикутник, чотирикутник (трапеція) і п'ятикутник не є рівними, то і діагоналі A1A4, A2A5, A3A6 та A1A3, A1A5, A2A6 і т.д., відповідно, не є рівними.
Отже, якщо у правильного многокутника всі діагоналі рівні, то він чотирикутник (квадрат) або п'ятикутник.
Відповідь: чотирикутник або п'ятикутник – Г.

Приклад 33.9 Кути п'ятикутника пропорційні до чисел 3, 5, 5, 6 і 8.
Знайти найбільший кут п'ятикутника.

Розв'язування: Використаємо формулу для обчислення суми внутрішніх кутів опуклого многокутника (n-кутника).
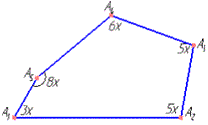 N=5, де ∠A1, ∠A2, ∠A3, ∠A4 , ∠A5- його внутрішні кути:
∠A1+∠A2+∠A3+∠A4+∠A5=180⁰(n-2)=180⁰(5-2)=540⁰.
Нехай x - коефіцієнт пропорційності, тоді ∠A1=3x, ∠A2=∠A3=5x, ∠A4=6x, ∠A5=8x.
Звідси отримаємо 3x+5x+6x+8x=540⁰, 27x=540⁰, x=20⁰.
Отже, ∠A5=8•20⁰=160 - найбільший кут заданого п'ятикутника.
Відповідь: 160⁰ – А.

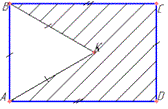
Приклад 33.10 На рисунку зображено прямокутник ABCD і рівносторонній трикутник ABK, периметри яких відповідно дорівнюють 20 см і 12 см. Знайти периметр п'ятикутника AKBCD.

Розв'язування: Маємо рівносторонній трикутник ABK, периметр якого P_ABK=12 см.
Тоді обчислимо довжину його сторони:
AB=AK=BK=P_ABK/3=12/3=4 см.
Маємо прямокутник ABCD, периметр якого P_ABCD=20 см і дві сторони AB=CD=4 см.
Тоді обчислимо довжину двох інших його сторін:
BC=AD=(PABCD-2AB):2=(20-2•4):2=12:2=6 см.
Маємо п'ятикутник AKBCD, у якого AK=BK=CD=5 см і BC=AD=6 см - довжини сторін.
Тоді обчислимо периметр п'ятикутника AKBCD:
P_AKBCD=3AK+2BC=3•4+2•6=12+12=24 см.
Відповідь: 24 – Б.

Приклад 33.10а Скільки діагоналей має многокутник, якщо сума його внутрішніх кутів дорівнює 1620⁰?

Розв'язування: Спочатку обчислимо кількість сторін (вершин) n многокутника, використовуючи формулу для обчислення суми внутрішніх кутів опуклого многокутника (n-кутника):
180⁰(n-2)=1620⁰, n-2=9, звідси n=11.

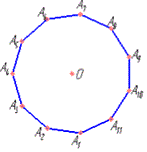
За формулою для обчислення кількості діагоналей многокутника обчислюємо

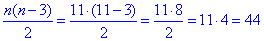
 одинадцятикутник має сорок чотири діагоналі.
Відповідь: 44 – Д.

Часто можна знайти задачі, де потрібно знайти не кількість всіх діагоналей, а лише скільки з них виходять з однієї вершини многокутника.
Наприклад, скільки діагоналей виходить з однієї вершини 11 кутника?
З малюнку за логікою знаємо, що в n - кутнику з однієї вершини можна провести (n-3) діагоналі, тому що з'єднавши вершину з сусідніми вершинами не отримаємо діагоналі та й саму вершину відкидаємо.
Таким чином з однієї вершини 11-кутника можна провести 8 діагоналей.
За тим же алгоритмом з однієї вершини 10 кутника можна провести 7 діагоналей,
з однієї вершини 15 кутника можна провести 12 діагоналей,
з однієї вершини 8-кутника можна провести 5 діагоналей, і т.д.

Приклад 33.18 Скільки сторін має опуклий многокутник, у якого сума внутрішніх кутів дорівнює сумі його зовнішніх кутів, узятих по одному при кожній вершині?

Розв'язування: Маємо 180⁰(n-2) - сума всіх внутрішніх кутів многокутника;
180⁰(n-2)/n - величина внутрішнього кута і 180⁰-180(⁰n-2)/n - величина зовнішнього кута многокутника, тоді 180⁰n-180⁰(n-2)=360⁰.
- сума зовнішніх кутів многокутника, взятих по одному при кожній вершині.
Отже, за умовою задачі отримаємо 180⁰(n-2)=360⁰, n-2=2, звідси n=4.
Відповідь: чотири – Б.

Більше задач на радіуси та кути многокутників Ви можете знайти в наступних уроках.

Вас може зацікавити:
1. Многокутники. ЗНО відповіді
2. Шестикутник. Формули, властивості, приклади
3. Площа рівнобічної трапеції
4. Ромб. Формули площі і радіуса вписаного кола
5. Площа трикутника. Формули