Коло вписане у ромб. Радіус кола

Означення вписаного кола: Коло, що дотикається до всіх сторін ромба та має центр на перетині діагоналей ромба називається вписаним у ромб колом.

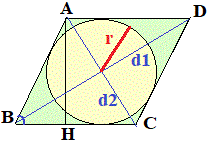
Формули радіуса вписаного кола:

• Радіус вписаного кола рівний половині висоти ромба:
  r=h/2 (1)
• радіуса кола, вписаного в ромб, рівний площі поділеній на подвоєну довжину сторони:
  r=S/(2a) (2)
• Радіуса вписаного кола, через площу та кут ромба:
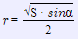  (3)
• Радіуса кола, вписаного в ромб, через сторону і кут:
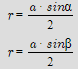  (4)
• Формули радіуса вписаного кола, через діагоналі ромба та синус кута:
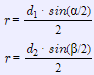  (5)
• Формула радіуса кола, вписаного в ромб, через дві діагоналі:
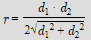  (6)
• Формула радіуса кола, вписаного в ромб, через дві діагоналі та сторону:
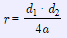  (7)

Задачі на площу, сторони, радіус, діагоналі ромба з вписаним колом

Приклад 1. Сторона ромба дорівнює 10 см, а одна з діагоналей 12 см знайдіть радіус вписаного в ромб кола.​
Розв'язування: За формулою (7) радіус вписаного кола в ромб рівний добутку його діагоналей поділеному на периметр ромба:
r=d1*d2/(4*a).
Другу діагональ ромба знайдемо, як подвоєний катет прямокутного трикутника

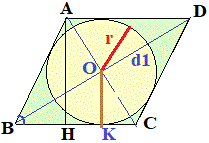
d1=12, BC=a=10.
За теоремою Піфагора для прямокутного ΔBOC:
(d1/2)^2+(d2/2)^2=a^2,
(12/2)^2+(d2/2)^2=10^2,
36+(d2/2)^2=100,
(d2/2)^2=100-36=64=8^2,
d2/2=8 см.
Друга діагональ ромба
d2=16 см
Обчислюємо радіус вписаного кола за формулою:
r=d1*d2/(4*a),
r=(12*16)/(4*10)=4,8 см.
Відповідь: 4.8 см.

Приклад 2. Сторона ромба дорівнює 8 см. Радіус кола, вписаного в ромб дорівнює 2. Знайти гострий кут ромба.
Розв'язування: Нехай дано ромб ABCD (кут ∠ B - гострий), проводимо висоту AH до сторони BC, трикутник ABH прямокутний/

За властивістю вписаного в ромб кола
AH=2*r=2*2=4 см.
Оскільки катет АН =1/2*AB рівний половині гіпотенузи, тоді він лежить навпроти кута π/6.
Кут ∠B=30⁰.
Відповідь: 30⁰.

Приклад 3. Точка дотику кола, вписаного в ромб, поділяє сторону ромба відрізки 16 дм і 9 дм. Обчисліть діаметр кола.​
Розв'язування: Побудуємо ромб з вписаним колом. Точка дотику K кола з ромбом ділить сторону BC на відрізки:
BK=16, KC=9.

Трикутник ΔBOC, побудований на половинах діагоналей ромба та стороні - прямокутний.
Відрізок OK - радіус кола.
За властивістю висоти, опущеної на гіпотенузу прямокутного трикутника вона рівна середньому геометричному відрізків, на які ділить гіпотенузу.
Тобто, r²=BK*KC=16*9=144=12².
Звідси r =12 см,
Обчислюємо діаметр кола вписаного в ромб
D=2r=2*12=24 см.
Відповідь: 24 см.

Приклад 4. Точка дотику кола, вписаного в ромб, поділяє сторону ромба відрізки 4 см і 16 см. Обчисліть площу ромба.​
Розв'язування: Скористаємося результатами попередньої задачі. Побудуємо ромб, сторона ромба BC точкою дотику поділена на відрізки:
BK=16 см, KC=4 см.

За властивістю висоти, опущеної до гіпотенузи трикутника
r²=BK*KC=16*4=64=8².
h=r =8 см.
Площу ромба знайдемо через площу 4 прямокутних трикутників ΔBOC:
S=4*1/2*BC*h=2*8*(16+4)=2*12=320 см. кв.
Відповідь: 320 см².

Приклад 5. Більша діагональ ромба дорівнює 24 см, а радіус вписаного кола - 6 см. Обчислити площу ромба та меншу діагональ.​
Розв'язування: Виконаємо допоміжний рисунок.
Нехай BD=24 см, r=OK=6 см.

Розглянемо прямокутний трикутник ΔBOC.
BO=BD/2=24/2=12 см.
Виразимо гострий кут ромба через кут ∠OBK прямокутного трикутника
∠B=2*∠OBK.
∠OBK знайдемо з формули синуса:
sin(∠OBK)=OK/OB=2r/d1=6/12=0.5.
Звідси ∠OBK=30⁰,
∠B=2*∠OBK=60⁰.
Далі є два методи, шукати площу ромба через площу 4 трикутників. Для цього нам достатньо виразити KC з формули
r²=BK*KC, та знайти довжину сторони ромба:
BC=BK+KC.
Другий метод, виразити площу ромба через сторону та кут ромба з формули (3):
S=4r^2/sin(∠B),
S=4*6^2/sin(60⁰)=4*36*2/√3=
= 288/√3 =288√3/3=96√3=166,3 см. кв.
Відповідь: 96√3 см².

Приклад 6. Тупий кут ромба дорівнює 150 градусів. Радіус кола вписаного в цей ромб дорівнює 10 см. Обчисліть площу ромба.
Розв'язування: Формула радіуса вписаного в ромб кола:
r=H/2, звідси висота ромба
Н=2r=2*10=20 см.
Розпишемо формули площі ромба
прирівняємо S=a*H і S=a²*sin(α):
а*Н=a²*sin(α),
Н=a*sin(α),
а=Н/sin(α)=20/sin(150⁰)=20/(1/2)=40 см.
Знайдемо площу ромба через добуток сторони на висоту:
S=40*20=800 см. кв.
Відповідь: 800 см².

Приклад 7. Гострий кут ромба 45 градусів, радіус кола, вписаного в ромб  дорівнює √2 см. Обчислити периметр та площу ромба..
Розв'язування: За радіусом вписаного кола знайдемо діагоналі ромба:
D/2 = R*cos(α/2);
d/2 = R*sin(α/2)
Використаємо формулу площі ромба через півдобуток діагоналей, щоб звести до синуса подвійного кута:
S=D*d/2=R²*sin(α)=(√2)²*√2/2 =√2 см².
За другою формулою площа ромба рівна
S = a*h.
Висота ромба через радіус вписаного кола
h =2R=2√2 cм.
Знайдемо сторону ромба
a=S/h=√2/(2√2)=0,5 cм.
Обчислюємо периметр ромба
P=4a=2 см.
Відповідь:P=2 см.

Попереду Вас чекають нові готові завдання з геометрії, які навчать обчислювати всеможливі характеристики фігур. Вчіть формули, схеми обчислень, застосовуйте кращі методики для швидкого обчислення правильних відповідей.