Задачі на призми зі Сканаві

До вашої уваги три готові задачі на призми, які задавали на практикумі з елементарної геометрії /Стереометрія/ Частина І «Призма».
Завдання не надто складні, проте як мінімум теорему косинусів та Піфагоро обов'язково потрібно знати, щоб розуміти про що йдеться в поясненнях до завдань.
Номера після 11. відповідають основним завданням зі збірника за ред. М. І. Сканаві.

Задача 11.107 Об'єм правильної восьмикутної призми дорівнює 8м³, а її висота дорівнює 2,2 м. Знайти бічну поверхню призми.
Розв'язання: Перш ніж що небудь обчислювати в геометричних задачах слід виконати побудова, це запам'ятайте.
Друге правило - правильно виконана побудова рисунку до задачі містить 50% відповіді.
Правило має деяке перебільшення, однак без просторового уявлення що шукаємо часто важко уявити що відповідь може бути настільки проста.
Тому "косо-криво" виконуйте допоміжну побудову, аналізуйте геометрію і думайте, яку теорему і де слід застосовувати.
Ми ж намагаємося зробити рисунки максимально інформативними, то ж відповіді та поясненням повинні бути простими для більшості з Вас.
І так, побудуємо просторовий рисунок восьмикутної призми

1) Розглянемо її основу – восьмикутник A₁A₂..A₈.

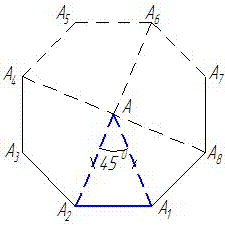
Площа восьмикутника – рівна площі основи призми Soc (тут V=8m3, H=2,2 m), тому з формули об'єму знаходимо її значення: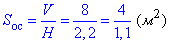

Оскільки правильний восьмикутник розбивається своїми діагоналями на вісім рівних (рівнобедрених) трикутників (за властивістю), то знаходимо площу одного такого трикутника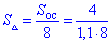

Після спрощень площа трикутника рівна 0,45(45)

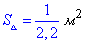
2) Розглянемо рівнобедрений трикутник AA₁A₂, у якого S=1/2,2, AA₁=AA₂ (рівні як радіуси описаного кола) і кут рівний 45 градусів

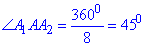
Знайдемо сторону A₁A₂ – сторону правильного восьмикутника (основи призми).
Із формули площі трикутника маємо залежність:

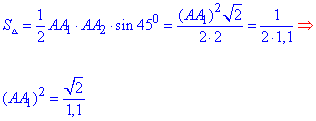
За теоремою косинусів знайдемо сторону A₁A₂: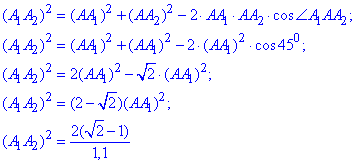

Довжина сторони правильного восьмикутника рівна

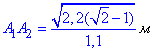
3) Знайдемо бічну поверхню призми за формулою добутку периметра основи на висоту S_b=P_oc•H.

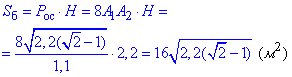
Це всі пояснення до задачі на призму, якщо не користуватися математичним довідником чи інтернетом.
Наведемо інше пояснення до прикладу.

ІІ – спосіб:

1) Площу одного з трикутників, на які розбивається восьмикутник знаходити не потрібно!
Можна зразу скористатися формулою для обчислення площі многокутників:

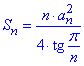
Для заданого восьмикутника (n=8 і a=A₁A₂) маємо

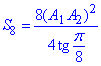
Прирівняємо наші площі (Soc=S₈):

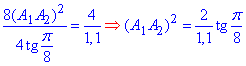
Знайдемо значення тангенса tg(Pi/8), використовуючи тригонометричну тотожність для тангенса половини кута tg(x/2):
.
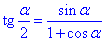Для кута 45 градусів 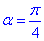маємо:

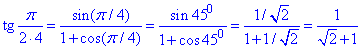
Остаточно знаходимо сторону правильного восьмикутника A₁A₂: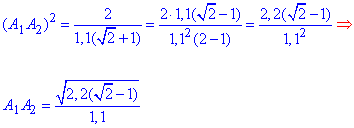

Зауваження: тут треба знати, як виводиться формула для площі правильних многокутників S_n.

Задача 11.110 Знайти відстань між серединами двох мимобіжних ребер куба, повна поверхня якого дорівнює 36 cm².
Розв'язання: 1) Перш за все виконуємо допоміжний рисунок та виділяємо частину, що нас цікавить

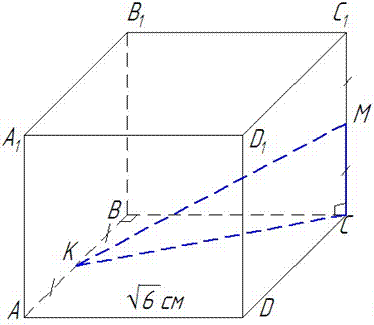
Запишемо формулу для обчислення площі повної поверхні куба: Sп.п.=6a², оскільки куб має шість граней однакової площі.
Звідси сторона куба рівна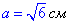

2) Розглянемо основу куба – квадрат ABCD, де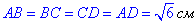

За умовою задачі:

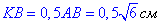
Із прямокутного трикутника KBC маємо

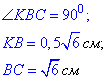
за теоремою Піфагора знайдемо квадрат гіпотенузи KC²:
KC²=KB²+BC², звідки KC²=0.25•6+6=1.5+6, тобто KC²=7.5.

3) Розглянемо прямокутний трикутник MCK, у якого KC=7,52;
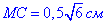(за умовою задачі), <MCK=90^o.
Прямі 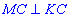перпендикулярні за теоремою про перпендикулярність прямої і площини.
За теоремою Піфагора знайдемо гіпотенузу MK – відстань між серединами двох мимобіжних ребер AB і CC₁:
MK²=KC²+MC², MK²=7.5+1.5=9, звідси MK=3.
На цьому задача розв'язана.

Задача 11.113 У похилому паралелепіпеді проекція бічного ребра на площину основи дорівнює 5 дм, а висота дорівнює 12 дм.
Переріз, перпендикулярний до бічного ребра – ромб з площею 24 дм² і діагоналлю 8 дм.
Знайти бічну поверхню й об'єм паралелепіпеда.
Розв'язання: 1) Графічно зобразимо заданий паралелепіпед та переріз.
Розглянемо перпендикулярний переріз паралелепіпеда ABCDA1B1C1D1 – ромб KLMN, у якого S_KLMN=24 дм² – площа і NL=8 дм – діагональ ромба.

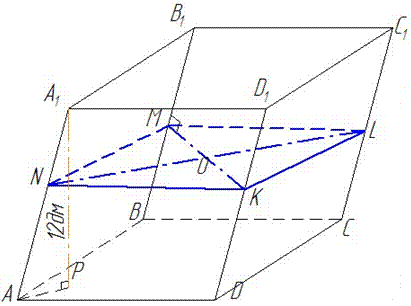
Знайдемо другу діагональ і сторону ромба (у ромба всі сторони рівні).
За властивістю ромба (як паралелограма) діагоналі в точці перетину діляться навпіл (див. рисунок);

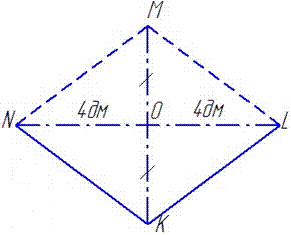
діагоналі ромба перетинаються під прямим кутом 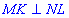, тому кут рывний 90 градусів

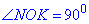
Маємо NL=2•ON=8 дм, звідси ON=4 дм, а MK=2•OK.
Знайдемо OK.
S_KLMN=2•ON•OK, звідси 8•OK=24, тому OK=3 дм.
Із прямокутного трикутника 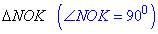за теоремою Піфагора знайдемо NK:

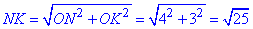
отже NK=5 дм – сторона ромба KLMN.
Периметр ромба рівний 20 дм:

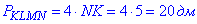
2) Опустимо висоту AP паралелепіпеда на площину основи ABCD і розглянемо трикутник APA1, у якого AP=5 дм – проекція бічного ребра AA1 на площину основи ABCD і A1P=12дм – висота паралелепіпеда ABCDA1B1C1D1.

Оскільки сторона перпендикулярна до пощини 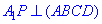, то кут рівний 90 градусів і трикутник 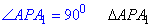– прямокутний.
Знайдемо AA1 за теоремою Піфагора:

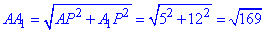
отже AA1=13 дм – довжина бічного ребра паралелепіпеда.

3) Знайдемо бічну поверхню і об'єм заданого паралелепіпеда.
Бічна поверхня похилого паралелепіпеда – добуток периметра перпендикулярного перерізу і довжини бічного ребра:
S_б=P_KLMN•AA1.
Отже бічна площа паралеепіпеда рівна

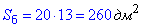
Об'єм похилого паралелепіпеда – добуток площі перпендикулярного перерізу і довжини бічного ребра:
V=S_KLMN•AA1.
Отже, обєм параелепіпеда рівний 312 дм³

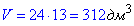
На цьому пояснення закінчуються та не закінчуються задачі, які розв'язані щоб допомогти Вам у навчанні.
Практикум виконано на відмінно та із "зараховано" у заліковці можна сміло йти на канікули!