Розглянемо готові відповіді до тестових завдань із ЗНО підготовки на знаходження площі поверхні кулі (сфери).
Формула площі поверхні кулі рівна чотирикратному значенню площі круга, проведеного через центр кулі.
Сама по собі формула проста, набагато складніше виразити радіус кулі через задані в умовах задач величини.
Задача 40.4 Діаметр кулі дорівнює 6 см. Знайти площу поверхні кулі.
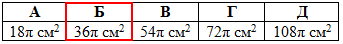
Розв'язання: Дане завдання є класикою із шкільної геометрії та вимагає знання всього однієї простої формули, яку тут буде застосовано багаторазово.
Площу поверхні кулі знаходять за формулою:
S=4πR2, де R– радіус кулі.
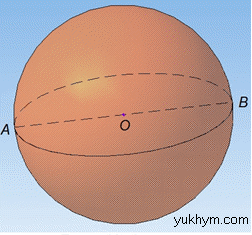
Маємо кулю з центром в точці O і діаметром AB=D=2R=6 см.
Звідси встановлюємо, що R=AO=BO=D/2=3 см – радіус заданої кулі.
Підставляємо радіус у формулу площі поверхні кулі:
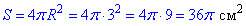
отже S=36π см2.
Відповідь: 36π см2 – Б.
Задача 40.5 Площина перетинає сферу. Довжина лінії перетину дорівнює 10π см, а діаметр сфери, проведений в одну з точок лінії перетину, утворює з площиною перетину кут 60. Знайти площу поверхні сфери.
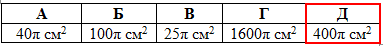

Розв'язання: Ще раз нагадуємо, що формула площі поверхні сфери має вигляд:
S=4πR2, де R– радіус сфери.
Маємо сферу з центром в точці O і радіусом R=AO.
Площина, яка перетинає сферу, перетинає її по колу. Тому маємо коло (лінію перетину площини та сфери) з центром в точці O1 і радіусом R1=AO1.
За умовою задачі, довжина кола:
C=10π см, але C=2πR1, 10π=2πR1 звідси знаходимо радіус круга R1=AO1=5 см.
За умовою задачі, ∠OAO1=60 – кут між діаметром (радіусом R=AO) сфери з площиною перетину (тобто колом з центром в точці O1).
Відрізок OO1 – відстань від центра сфери до площини перерізу, тому OO1⊥AO1.
Розглянемо прямокутний ΔOAO1 (∠OO1A=90), у якого AO1=5 см – прилеглий катет до кута ∠OAO1=60.
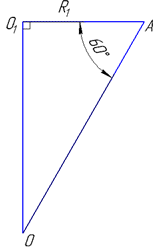
За означенням косинуса гострого кута прямокутного трикутника знайдемо гіпотенузу AO=R – радіус сфери:
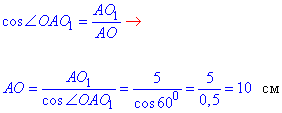
Отже, R=AO=10 см – радіус сфери.
Площа поверхні сфери рівна:
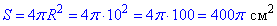
Відповідь: 400π см2 – Д.
Задача 40.7 Об'єми двох куль відносяться як 27:125.
Як відносяться площі їх поверхонь?
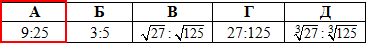
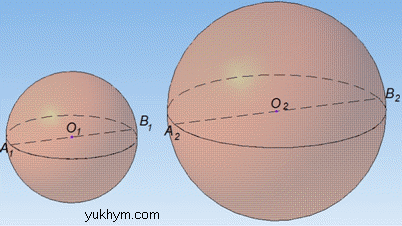
Розв'язання: Відношення об'ємів двох куль дорівнює відношенню кубів їх відповідних лінійних розмірів (наприклад радіусів).
Нехай R1 і V1 – відповідно радіус і об'єм І (тобто «малої») кулі;
R2 і V2 – відповідно радіус і об'єм ІІ (тобто «великої») кулі, тоді справедливе співвідношення
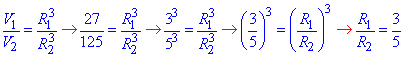
Відношення площ двох куль дорівнює відношенню квадратів їх відповідних лінійних розмірів.
Нехай S1 – площа поверхні І (тобто «малої») кулі;
S2 – площа поверхні ІІ (тобто «великої») кулі, тоді
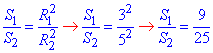
звідси S1:S2=9:25.
ІІ спосіб:
Враховуючи вище викладене, визначаємо відношення площ:
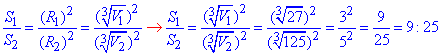
Відповідь: 9:25 – А.
Задача 40.11 Металеву кулю переплавлено на 8 рівних куль.
Як змінилася при цьому загальна поверхня?

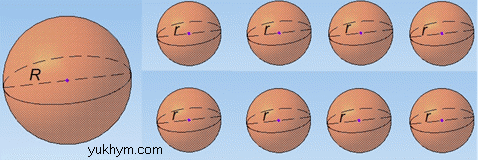
Розв'язання: Маємо велику кулю з радіусом R, яку потім переплавили на 8 «малих» куль з радіусом r.
Це означає, що об'єм «великої» кулі розділили на 8 «малих» куль.
Площа поверхні «великої» кулі:
S1=4πR2.
Об'єм «великої» кулі: V1=4/3•πR3.
Об'єм «малої» кулі: V2=4/3•πr3.
Оскільки з однієї «великої» кулі зробили 8 рівних «малих» куль, то об'єм «малої» кулі становить 1/8 частину об'єму «великої» кулі, тобто
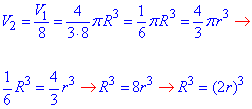
отримали, що R=2r – радіус «великої» кулі вдвічі більший, ніж радіус «малої» кулі, або r=R/2.
Площа поверхні однієї «малої» кулі:
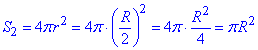
Загальна площа поверхні 8 «малих» куль:
8S2=8πR2.
Звідси маємо
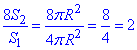
Це означає, що загальна поверхня всіх «малих» куль збільшилась удвічі у порівнянні з однією «великою» кулею.
Відповідь: збільшилась удвічі – Б.
Задача 40.17 Знайти відношення площ поверхні куба і вписаної в нього кулі.
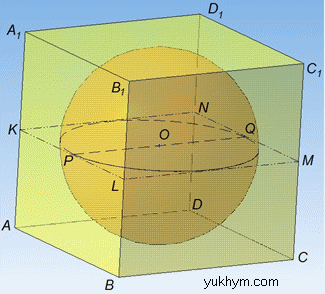
Розв'язання: Маємо куб ABCDA1B1C1D1 і вписану в нього кулю з центром O. Нехай ребро куба (у куба всі ребра рівні за означенням) дорівнює a.
Куля вписана у куб, якщо куля дотикається до всіх граней куба (за означенням).
Куля вписана у куб, якщо великий круг кулі є вписаним у квадрат, який є одним і перерізів куба (за властивістю).
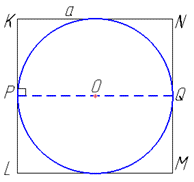
Нехай великий круг кулі з центром O вписаний у квадрат KLMN, довжина сторони якого дорівнює довжині ребра куба, тобто a.
Тоді за властивістю круга вписаного в квадрат: діаметр круга PQ дорівнює стороні квадрата, D=PQ=KN=a (круг дотикається до сторін квадрата і в точці дотику радіус круга перпендикулярний до сторін квадрата, тому PQNK – прямокутник).
Але діаметр великого круга дорівнює діаметру кулі (за властивістю). Тому D=a – діаметр вписаної у куб кулі, R=D/2=a/2 – радіус заданої кулі.
Площа поверхні куба ABCDA1B1C1D1:
Sп.п.=6a2
(у куба всі грані рівні, тому площу однієї з них помножили на їх кількість – 6);
Площа поверхні вписаної в куб кулі:
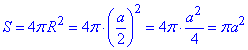
Відношення площ поверхні куба і вписаної в нього кулі:
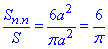
Відповідь: 6/π – Г.
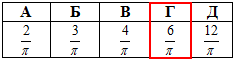
Задача 40.23 Установити відповідність між геометричними тілами (1–4) та формулами для відшукання їх поверхонь (А–Д).
1. Циліндр
2. Куля
3. Конус
4. Правильна чотирикутна піраміда
А. πr(r+l)
Б. 4πr^2
В. a(a+2l)
Г. 2πr(r+l)
Д. 2πrl
Розв'язання: Формули для відшукання площ поверхонь для заданих геометричних тіл використовувались у розділах 37 – 40, тому їх напишемо без доведень, де
r – радіус: основи циліндра для S1, основи конуса для S3 і кулі для S2;
l – твірна: циліндра (вона ж і висота) для S1, конуса для S3;
апофема піраміди для S2;
a – сторона основи (квадрата) правильної чотирикутної піраміди для  .
.
1. Циліндр: S1=2Soc+Sb=2•πr2+2πrl=2πr(r+l), Г;
2. Куля: S2=4πr2, Б;
3. Конус: S3=Soc+Sb= πr^2+πrl=πr(r+l), А;
4. Правильна чотирикутна піраміда: S4=Soc+Sb=a2+1/2•4al=a(a+2l), В.
Інші задачі на об'єм кулі, площі перерізів та ін. наведені в наступних публікаціях.


