Продовжуємо аналізувати готові задачі із ЗНО підготовки на кулю. Сьогодні розберемо типові завдання з геометрії на знаходження площі перерізу кулі площиною.
Завдання самі по собі досить цікаві, одні зводяться до застосування теореми Піфагора, інші вимагають складання системи двох рівнянь за формулою Піфагора для вираження невідомих розмірів, а вже тоді визначення радіуса кулі і на його основі площі перерізу кулі (круга) або площі поверхні кулі.
Завдання найбільш потрібні учням 10-11 класів для розуміння практичної сторони таких прикладів, та для усіх хто стикнувся з необхідністю вирішити подібні задачі.
Задача 40.1 Кулю, радіус якої 5 см, перетнуто площиною, що розміщена на відстані 3 см від центра.
Знайти площу перерізу.
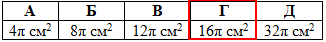
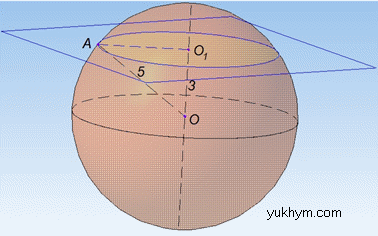
Розв'язання: Переріз кулі будь-якою площиною (тобто на будь-якій відстані від центра кулі та під будь-яким кутом) завжди буде круг, а лінія перетину сфери та площини – колом.
Відстань від центра кулі до перерізу – перпендикуляр опущений з центра кулі до центра кругу, який є перерізом.
З побудови маємо: кулю з радіусом R=AO=5 см, круг з радіусом r=AO1 і OO1=3 см – відстань від центра кулі до перерізу (OO1⊥AO).
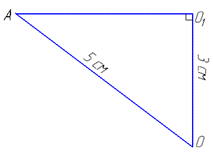
З прямокутного трикутника AO1O (∠AO10=90), в якому OO1=3 см – катет і AO=5 см – гіпотенуза, за теоремою Піфагора знайдемо катет AO1=r – радіус круга – перерізу кулі площиною:
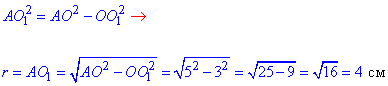
Площа круга рівна:
Sпер=πr2=16π
Завдань звелося до застосування однієї з поширених в геометрії формули, а все тому, що правильно розтлумачена умова завдання та виконаний рисунок. Добре зроблений рисунок, як правило, містить багато інформації, що і як далі робити?
Відповідь: 16π см2 – Г.
Задача 40.6 Відстань між рівновеликими паралельними перерізами кулі, радіус якої становить 10 см, дорівнює 12 см.
Знайти площу кожного з цих перерізів.
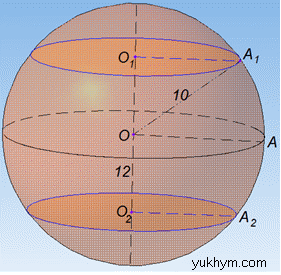
Розв'язання: Маємо кулю з центром в точці O та радіусом R=AO.
Площина, яка перетинає кулю, перетинає її по кругу. Оскільки паралельні перерізи рівновеликі (за умовою), тобто їх площі рівні, тому відстань від центра кулі до кожного перерізу є однакова (за властивістю пропорційності площ паралельних перерізів і відстаней між центром кулі), тобто
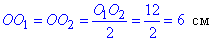
де OO1=12 см – відстань між паралельними перерізами за умовою задачі, звідси слідує, що OO1⊥A1O1 і OO2⊥A2O2.
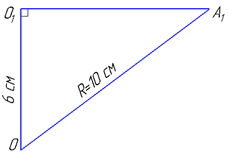
Тому, щоб знайти площі перерізів достатньо розглянути один переріз, наприклад круг з центром в точці O1 і прямокутний трикутник A1O1O.
За теоремою Піфагора знайдемо катет A1O1=r – радіус круга – перерізів кулі площинами (з прямокутного трикутника A1O1O (∠A1O1O=90), в якому OO1=6 см – катет і A1O=10 см – гіпотенуза):
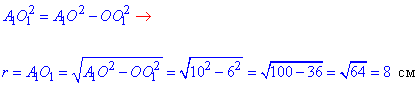
Площа перерізів, (площа круга) рівна:
Sпер=πr2=64π см2.
Відповідь: 64π см2 – В.
Задача 40.27 Перерізи кулі двома паралельними площинами, між якими лежить центр кулі, мають площі 144π см2 і 25π см2.
Відстань між площинами дорівнює 17 см.
Знайти у квадратних сантиметрах площу S поверхні кулі.
У відповідь записати S/π.
Розв'язання: Площу поверхні кулі обчислюють за формулою:
S=4πR2, де R – радіус кулі.
Запам'ятайте, що площа поверхні кулі (сфери) рівна площі 4 кругів проведених через центр кулі.
Площа круга всім відома з шкільної геометрії за 9-11, її важко забути. Множимо її на 4 і отримуємо формулу площу поверхні кулі (сфери).
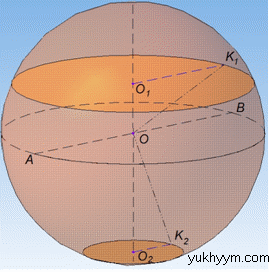
Маємо кулю з центром в точці O і перерізами у вигляді кругів з центрами O1, O2 і площами S1=144π см2, S2=25π см2 відповідно.
Нехай R1=O1K1, R2=O2K2 – відповідно радіуси І і ІІ кругів, тоді O1O2=17 см – відстань між перерізами (кругами), тоді O1O2⊥O1K1, O1O2⊥O2K2.
Оскільки площа круга S=πR2, то маємо:
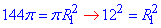, звідси R1=O1K1=12 см – радіус І круга;
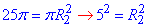, звідси R2=O2K2=5 см – радіус ІІ круга.
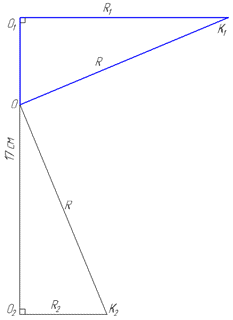
Дослідимо прямокутні трикутники OO1K1 (∠OO1K1=90) та OO2K2 (∠OO2K2=90), у яких OK1=OK2=R – гіпотенузи (рівні);
R1=O1K1=12 см, R2=O2K2=5 см і OO1, OO2 – відповідні катети.
Складаємо залежності для відрізків O1O2=17 см, тоді нехай OO1=x, а OO2=17-x.
Тоді за теоремою Піфагора для відповідних прямокутних трикутників складемо систему рівнянь:
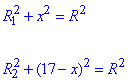
Прирівняємо отримані вирази та знайдемо OO1=x:
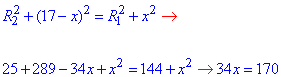
звідси OO1=x=170/34=5 см.
За теоремою Піфагора у прямокутному ΔOO1K1 знайдемо гіпотенузу OK1=R:
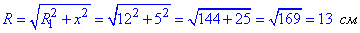– радіус кулі.
Обчислюємо площу поверхні кулі:
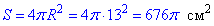
S/π=676.
Відповідь: 676.
Задача 40.28 Перерізи сфери двома паралельними площинами мають довжини 10π см і 24π см.
Знайти у квадратних сантиметрах площу S поверхні сфери, якщо відстань між площинами дорівнює 7 см і центри перерізів лежать на одному радіусі сфери.
У відповідь записати S/π.
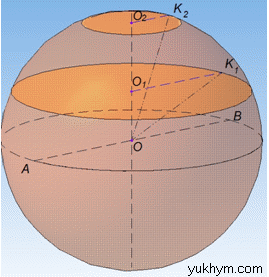
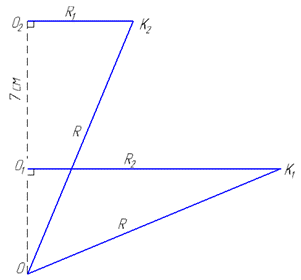
Розв'язання: Площу поверхні сфери обчислюють за формулою:
S=4πR2, де R – радіус сфери.
Маємо сферу з центром в точці O і перерізами у вигляді кіл з центрами O1, O2 і довжинами C1=24π см, C2=10π см відповідно.
Нехай R1=O1K1, R2=O2K2 – відповідно радіуси І і ІІ кіл, тоді O1O2=7 см – відстань між перерізами, тоді O1O2⊥O1K1, O1O2⊥O2K2.
Оскільки довжина кола Ci=2πRi, то маємо:
24π=2 π R1, 2 π •12=2 π •R1, звідси R1=O1K1=12 см – радіус І кола
10π=2 π R2, 2 π •5=2 π •R2, звідси R2=O2K2=5 см – радіус ІІ кола.
Розглянемо прямокутні трикутники OO1K1 (∠OO1K1=90) і OO2K2 (∠OO2K2=90), у яких OK1=OK2=R – гіпотенузи (рівні);
R1=O1K1=12 см, R2=OK2=5 см і OO1, OO2 – відповідні катети.
Оскільки O1O2=7 см, тоді позначимо OO1=x, а OO2=7+x, так як за умовою задачі центри перерізів лежать на одному радіусі сфери.
Далі на основі формули Піфагора з прямокутних трикутників складаємо систему двох рівнянь:
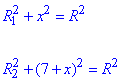
Прирівняємо ліві частини до знаку рівності та виражаємо OO1=x:
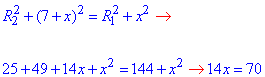
звідси OO1=x=70/14=5 см.
Гіпотенузу OK1=R у прямокутному ΔOO1K1 знайдемо за теоремою Піфагора :
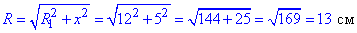– радіус кулі.
Площа поверхні кулі:
S=4πR2=4π•132=676π см2,
S/π=676.
Відповідь: 676.
Більше готових задач на кулю та інші геометричні фігури Ви можете переглянути в категорії Геометрія. Якщо Ви маєте цікаві завдання, які за суттю відрізняються від розглянутих тут, тоді просимо їх нам надсилати, щоб ми мали нагоду доповнити цю статтю та краще розкрити Вам задану тему.
