Сьогодні розберемо кілька готових відповідей до задач на об'єм кулі. Формула об'єму кулі достатньо проста, в цьому Ви скоро переконаєтесь з пояснень до завдань.
Наведені далі приклади взяті з одного із збірників для ЗНО підготовки з математики. Відповіді будуть корисними як для школярів 10-11 класів, так і всіх, хто призабув формули з геометрії.
Красиві тримірні рисунки за умовами задач допоможуть швидше розібратися - "що відомо?, та Що потрібно знайти?"
Задача 40.3 Площа великого круга кулі дорівнює 4π см2.
Знайти об'єм кулі.
Розв'язання: Об'єм кулі обчислюють за формулою:
V=4/3πR3, де R – радіус кулі.
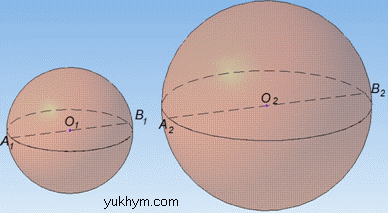
Маємо кулю з центром в точці O і діаметром AB=D=2R.
Великий круг кулі – це круг, у якого центр співпадає з центром кулі, а радіус (діаметр) великого круга дорівнює радіусу (діаметру) кулі.
Площу круга запишемо формулою:
S=πR2=4π см2, звідси πR2=4π, R2=4, отже R=2 см – радіус великого круга, тобто радіус кулі.
Об'єм кулі через радіус рівний:
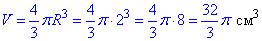
Це сама поширена формула кулі, тому добре її запам'ятайте.
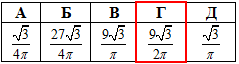
Відповідь: 32/3π см3 – Г.
Задача 40.8 Діаметр одного кавуна вдвічі більший від діаметра іншого.
У скільки разів перший кавун важчий від другого?
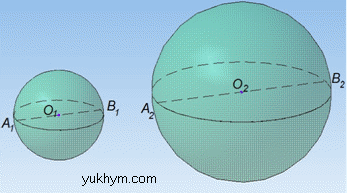
Розв'язання: В умові задачі задано кавуни, які мають однакову форму кулі та є однорідними за масою – це означає, що їх густини однакові, а відрізняються лише розмірами.
Зробимо математичну модель задачі: кавуни замінимо на кулі.
Оскільки кавуни є однорідними, то маси куль відносяться як їх об'єми відповідно, а відношення об'ємів куль дорівнює відношенню їх відповідних лінійних розмірів (наприклад діаметрів).
За умовою задачі маємо, що діаметр одного кавуна вдвічі більший за діаметр іншого, тобто D2=2D1.
Нехай m1, V1 і D1 – відповідно маса, об'єм і діаметр І (тобто «малої») кулі;
m2, V2 і D2– відповідно маса, об'єм і діаметр ІІ (тобто «великої») кулі, тоді
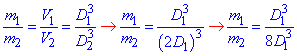
звідси m1/m2=1/8.
Отже, один кавун у 8 разів більший за інший.
Відповідь: 8 – Г.
Задача 40.24 Установити відповідність між відношеннями об'ємів двох куль (1–4) та відношеннями площ їх поверхонь (А–Д).
Розв'язання: (Розв'язок цієї задачі дивись у номері 40.7).
Встановимо відповідність між відношеннями об'ємів двох куль та відношеннями площ їх поверхонь за допомогою залежності
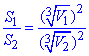
отриманої ІІ способом в задачі 40.7:
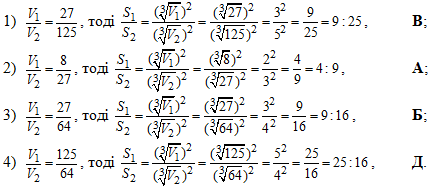
Задача 40.21 Навколо кулі описана правильна трикутна призма.
Знайти відношення об'ємів призми і кулі.
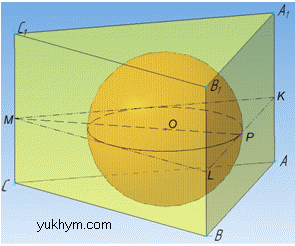
Розв'язання: Маємо правильну трикутну призму ABCA1B1C1 і вписану в неї кулю з центром O. Нехай ребро основи правильної трикутної призми дорівнює a.
Куля вписана у призму, якщо куля дотикається до всіх граней призми (за означенням).
Куля вписана у трикутну призму, якщо великий круг кулі є вписаним у правильний трикутник, який є одним і перерізів правильної трикутної призми, що проведений паралельно основам (за властивістю).
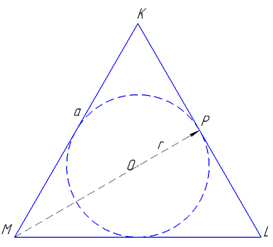
Нехай великий круг кулі з центром O описаний навколо правильного трикутника KLM, де KL=KM=LM=a, адже основи і перерізи призми, що проведені паралельно основам є рівними. Радіус великого круга (і одночасно кулі) r є радіусом круга, вписаного в правильний ΔKLM, звідси
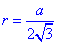– радіус кулі, вписаної в правильну трикутну призму.
Оскільки вписана куля дотикається до всіх граней правильної трикутної призми, то висота призми дорівнює діаметру кулі:
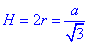
Об'єм правильної трикутної призми:
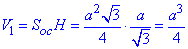
Об'єм кулі знаходимо за формулою:
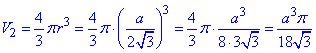
Отже,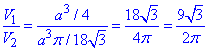 
– відношення об'ємів призми V1 і кулі V2.
Відповідь: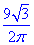 
– Г.
Задача 40.19 Знайти відношення об'ємів кулі та вписаного в неї куба.
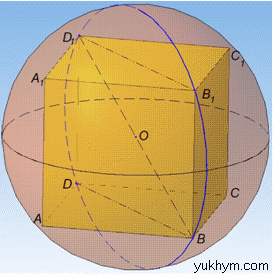
Розв'язання: Маємо кулю з центром O і вписаний в неї куб ABCDA1B1C1D1.
Нехай ребро куба (у куба всі ребра рівні за означенням) дорівнює a, тоді діагональ грані куба – a√2, а діагональ куба – a√3 (дивись розділ 36 «Призма»).
Куб вписаний у кулю, якщо всі вершини куба лежать на поверхні кулі (за означенням).
Куб вписаний у кулю, якщо діагональний переріз куба вписаний у великий круг кулі (за властивістю).
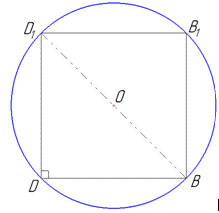
Нехай великий круг кулі з центром O описаний навколо діагонального перерізу куба – прямокутника BB1D1D, довжини сторін якого дорівнюють:
ребру куба BB1=DD1=a і діагоналі грані куба BD=B1D1=a√2.
Тоді діагональ BD1=a√3 прямокутника BB1D1D є діагоналлю куба.
За властивістю круга описаного навколо прямокутника:
діагональ прямокутника BB1D1D дорівнює діаметру (подвійному радіусу) описаного круга 2R=BD1=a√3.
Але радіус великого круга дорівнює радіусу кулі (за властивістю).
Тому R=√3/2•a – радіус описаної кулі навколо куба.
Знаходимо об'єм кулі:
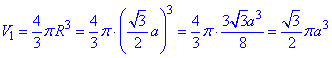
Об'єм куба:
V2=a3.
Відношення об'ємів кулі та вписаного в неї куба:
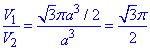
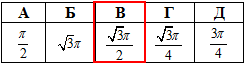
Відповідь: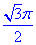 
– В.
Можна навести ще багато готових прикладів на об'єм кулі, але це вийде достатньо громіздка до читання стаття.
Тому подібні задачі на кулю (сферу) шукайте або в попередніх, або наступних публікаціях.
