Серед розглянутих раніше тестових задач на кулю із ЗНО підготовки нами відібрані 2, які важко віднести до розглянутих раніше тем.
Завдання вимагають застосування формули визначення довжини дуги кола. Можливо з часом таких завдань ми зберемо більше, а зараз просимо всіх охочих переглянути наведені далі відповіді.
Задача 40.9 М'яч, площа повної поверхні якого дорівнює 400π см2, зробив повний оберт по прямій. Знайти довжину шляху, яку він при цьому подолав.
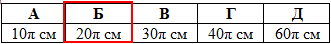
Розв'язання: Маємо м'яч з площею повної поверхні 400π см2.
Зробимо математичну модель задачі: м'яч замінимо на кулю.
Площу поверхні кулі обчислюють за формулою:
S=4πR2, де R– радіус кулі.
Але за умовою задачі S=400π, тобто 4πR2=400π, R2=100, звідси R=10 см.
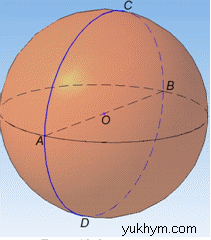
Оскільки м'яч (тобто куля) рухається по прямій і робить повний оберт (за умовою), то її траєкторією буде довжина великого кола, у якого центр і довжина діаметра співпадають з центром і довжиною діаметра самої кулі (на рисунку позначено синім кольором).
Довжина великого кола кулі:
C=2πR=2π▪10=20π см.
Отже, 20π см шляху подолав м'яч, зробивши повний оберт по прямій.
Відповідь: 20π см – Б.
Задача 40.10 На поверхні кулі радіуса r дано дві точки, відстань між якими дорівнює радіусу кулі. Визначити найкоротшу відстань на поверхні кулі між цими точками.
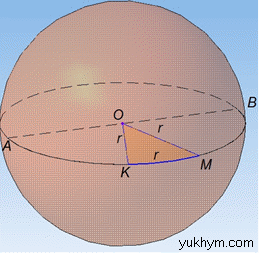
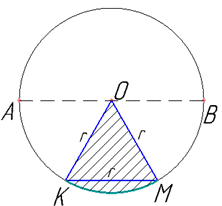
Розв'язання: Маємо кулю з радіусом r і двома точками M і K на її поверхні, відстань (по прямій) між якими MK=r.
Найкоротша відстань між точками M і K на поверхні кулі – це частина кола (тобто дуга), що обмежена радіусами MO і KO відповідно.
Тому можна розглядати сектор MKO з радіусом дуги r.
Розглянемо трикутник MKO. Маємо MO=KO=r як радіуси, а MK=r – відстань між точками M і K за умовою задачі.
Звідси випливає, що ΔMKO – рівносторонній, а тому його всі кути рівні і становлять 60 градусів, тобто ∠MOK=60 – центральний кут, що вписаний в дугу MK.
Тоді формулу довжини дуги подамо у вигляді:
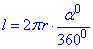тобто
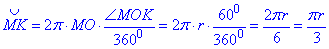
Отже,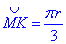 
– найкоротша відстань між точками M і K на поверхні кулі.
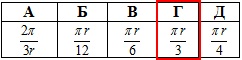
Відповідь: πr/3 – Г.
Якщо Ви маєте можливість доповнити дану статтю цікавими завданнями, то , будь-ласка, зробіть це!
Зараз дуже багато молоді використовує інтернет мережу для навчання, однак мало хто допомагає в підготовці публікацій.
