Формули та властивості шестикутника
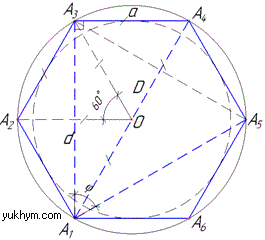Правильний шестикутник діагоналями ділиться на 6 рівносторонніх трикутників.
Усі кути при вершинах шестикутника рівні 120 градусів, центральний кут - 60 градусів.
Нехай маємо коло з центром у точці O.
Розділимо його на 6 рівних частин точками A1, A2, A3, A4, A5, A6 і послідовно з'єднаємо їх.
Отримали многокутник A1A2A3A4A5A6.
Проведемо радіуси цього кола в зазначені точки
A10=A2O=A3O=A4O=A5O=R.
Оскільки коло було розділено на 6 рівних частин, то кут між двома радіусами:
∠A1OA2=∠A2OA3=…=3600:6=600.
Трикутники A1OA2, A2OA3, A3OA4, ... є рівнобедреними (бічні сторони є радіусами кола) з кутом при вершині 600, тому за властивістю вони є рівними і рівносторонніми.
Звідси випливає, що отриманий многокутник A1A2A3A4A5A6 є правильним (рівностороннім) шестикутником, у якого a=A1A2=A2A3=…=A6A1 - довжина сторони, R=A1O=A2O=…=A6O - радіус описаного кола. Оскільки трикутники A1OA2, A2OA3, A3OA4,... рівні рівносторонні, то a=R.
Проведемо діагоналі A1A3, A1A4, A1A5 правильного шестикутника A1A2A3A4A5A6. У правильного шестикутника A1A2…A6 всі діагоналі (їх всього 9) розділяються на два типи:
більші, які проходять через центр шестикутника точку O, A1A4=A2A5=A3A6=D;
менші, які не проходять через центр шестикутника точку O, A1A3=A2A6=…=A4A6=d.
D=2R=2a, то більша діагональ є діаметром описаного кола і дорівнює 2a.
Далі можна доводити інші властивості правильного шестикутника, які тут та в наступних задачах не розписані, але використовуються!
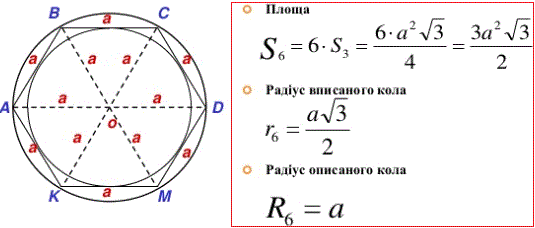
Найбільш часті формули шестикутника наведемо на рисунку, їх можете роздрукувати та мати під рукою при розв'язуванні задач.
ЗНО тести
Далі наведені відповіді до задач із ЗНО підготовки, що в умові або відповіді пов'язані із шестикутниками.
Приклад 33.11 Сторона правильного шестикутника дорівнює 10 см. Знайти його найбільшу діагональ.
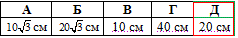Розв'язування: У правильного шестикутника маємо D=2a - більша діагональ, де a - сторона правильного шестикутника.
Таким чином, D=2•10=20 (см)
Відповідь: 20 см – Д.
Приклад 33.12 Сторона правильного шестикутника дорівнює a. Визначити меншу діагональ.
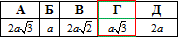
Розв'язування: У правильного шестикутника маємо d=a√3 - менша діагональ,
де a - сторона правильного шестикутника.
Відповідь: a√3 – Г.
Приклад 33.13 Сторона правильного шестикутника дорівнює 2 см. Знайти його площу.
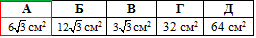
Розв'язування: Правильний шестикутник A1A2…A6 відрізками A1O=A2O=..A6O=R розбивається на 6 рівних рівносторонніх трикутників, наприклад ΔA2A3O. Це випливає з властивостей правильного шестикутника.
Площа правильного шестикутника A1A2…A6 дорівнює 6 площ правильного трикутника ΔA2A3O зі стороною a=2 см і кутом alpha=600 (у правильного трикутника всі кути рівні і дорівнюють 600).
На основі виведеної формули знаходимо площу шестикутника через трикутники
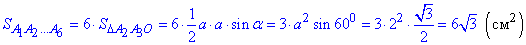
Відповідь: 6√3 см2 – А.
Приклад 33.14 Знайти периметр правильного шестикутника, якщо довжина кола, описаного навколо нього, дорівнює 18π см.
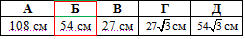
Розв'язування: У правильного шестикутника маємо R=a - радіус описаного кола, де a - сторона правильного шестикутника.
Отже, C=2PiR=18Pi - довжина описаного кола навколо правильного шестикутника, звідси радіус R=a=9.
Обчислимо периметр правильного шестикутника (як суму всіх його сторін):
P=6a=6•9=54 (см).
Відповідь: 54 см – Б.
Приклад 33.15 Знайти меншу діагональ правильного шестикутника, якщо більша його діагональ дорівнює 2√3см.
Розв'язування: У правильного шестикутника маємо D=2a - більша діагональ і d=a√3 - менша діагональ, де a - сторона правильного шестикутника.
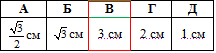
Підставляємо сторону a=D/2 в формулу меншої діагоналі шестикутника
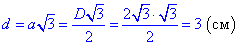
Відповідь: 3 см – В.
Приклад 33.16 Радіус кола, вписаного в правильний шестикутник, дорівнює 8√3см.
Знайти периметр шестикутника.
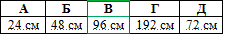
Розв'язування: У правильного шестикутника маємо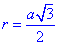 
- радіус вписаного кола, де a - сторона правильного шестикутника.
Звідси виражаємо сторону шестикутника через радіус вписаного в нього кола
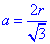
Маємо все для обчислення периметра шестикутника
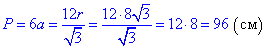
Відповідь: 96 см – В.
Приклад 33.17 Чому дорівнює найбільший кут між двома діагоналями, проведеними з однієї вершини правильного шестикутника?
Розв'язування: Маємо правильний шестикутник A1A2…A6. Проведемо діагоналі з однієї вершини A1, тобто d=A1A3=A1A5 і D=A1A4.
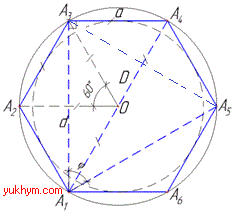
Тоді phi=∠A3A1A5 - найбільший кут між діагоналями, тобто між діагоналями A1A3 і A1A5.
Проведемо ще одну діагональ A3A5, причому d=A1A3=A1A5=A3A5.
Тоді трикутник A1A3A5 буде рівностороннім, звідси за властивістю кутів рівностороннього трикутника
.
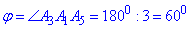Відповідь: 600 – Б.
Приклад 33.26 Три кути многокутника прямі, а решта дорівнюють по 1500.
Скільки найменше вершин може мати многокутник?
Розв'язування: Нехай n - кількість вершин (сторін, кутів) многокутника.
За умовою задачі три кути многокутника прямі, тобто дорівнюють по 900 означає, що їх сума дорівнює
3•900=2700.
Кожний з решти внутрішніх кутів - 1500 означає, що їх сума дорівнює
(n-3)•1500.
Загальна сума всіх внутрішніх кутів (будь-якого) многокутника
(n-2) •1800.
Складаємо та розв'язуємо рівняння
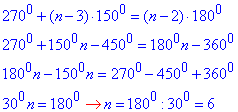
Робимо висновок, що заданий многокутник є шестикутником.
Відповідь: 6.
Приклад 33.30 Менша діагональ правильного шестикутника дорівнює √3.
Визначити:
1) його більшу діагональ;
2) периметр шестикутника.
Розв'язування: Наведемо рисунок шестикутника
Знайдемо сторону та більшу діагональ за формулою
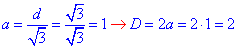
Обчислимо периметр правильного шестикутника:
P=6a=6.
Відповідь: 1) 2; 2) 6.
Приклад 33.31 R - радіус кола, описаного навколо правильного шестикутника.
Визначити радіус кола, вписаного в правильний шестикутник, якщо R=√3.
Розв'язування: У правильного шестикутника маємо R=a - радіус описаного кола і r=a√3/2 - радіус вписаного кола, де a - сторона правильного шестикутника.
Знаходимо радіус вписаного у шестикутник кола
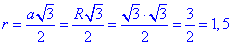
Відповідь: 1,5.
На ЗНО тестах Вас можуть чекати подібні за змістом, тільки інші за значеннями завдання. Тому добре вивчіть наведені в останніх трьох статтях схеми та формули. Добавте наш ресурс в закладки та використовуйте в навчанні. У нас багато практичного матеріалу як для студентів, так і для школярів та їхніх батьків.
