Продовжуємо розбирати відповіді ЗНО тестів на многокутники. Формули радіусів внутрішніх та зовнішніх кіл, кутів, діагоналей наведені в попередній статті та дублюються в ході обчислень наведених нижче задач.
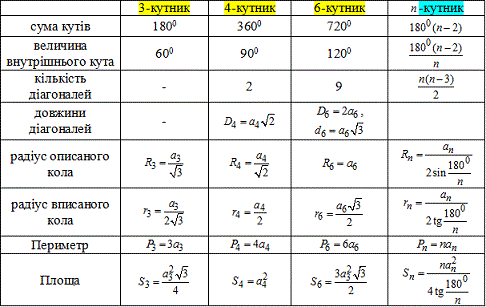
Приклад 1. Знайти величину внутрішнього кута 18 кутника, якщо всі його кути рівні.
Обчислення: Внутрішній кут знайдемо за формулою
180(n-2)/n, де n - кількість кутів.
Підставляємо
180*(18-2)/18=160 градусів.
Відповідь: 1600.
Приклад 2. Площа шестикутника 24√3 см2. Знайти сторону та периметр шестикутника.
Обчислення: Побудуємо шестикутник та наведемо основні його формули.
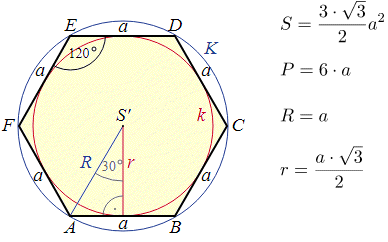
З формули площі
S=3√3a2/2
виразимо квадрат сторони
a2=2S/(3√3).
Підставляємо задану площу
a2=2*24√3/(3√3)=16=42 см2,
звідси сторона шестикутника рівна 4 см.
Обчислимо периметр
P=6a=6*4=24 см.
Відповідь: a=4 см, p=24 см.
Приклад 3. Скільки діагоналей у семикутника, восьмикутника, дев'ятикутника, дванадцятикутника?
Обчислення: Застосуємо формулу кількості діагоналей
N=(n-3)*n/2, де n - кількість сторін або кутів.
Знаходимо
N7=(7-3)*7/2=14;
N8=5*8/2=20;
N9=6*9/2=27;
N12=9*12/2=54.
У відповідь можемо записати, що у семикутника 14 діагоналей,
у восьмикутника - 20 діагоналей,
у 9-кутника - 27 діагоналей,
у дванадцятикутника 54 діагоналі.
Приклад 33.19 Скільки сторін має опуклий многокутник, якщо сума його усіх внутрішніх і усіх зовнішніх дорівнює 25200?
А | Б | В | Г | Д |
10 | 11 | 12 | 13 | 14 |
Розв'язування: Маємо 1800(n-2) - сума всіх внутрішніх кутів многокутника;
1800(n-2)/n - величина внутрішнього кута і 1800-1800(n-2)/n - величина зовнішнього кута многокутника,
тоді 1800n-1800(n-2)=3600 - сума зовнішніх кутів многокутника, взятих по одному при кожній вершині. Отже, за умовою задачі отримаємо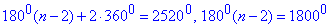 
n-2=10, звідси n=12.
Відповідь: 12 – В.
Приклад 33.20 Скільки вершин має правильний многокутник, у якого внутрішній кут у 8 разів більший від зовнішнього?
А | Б | В | Г | Д |
12 | 14 | 16 | 18 | 20 |
Розв'язування: Нехай x - величина внутрішнього кута, тоді 1800-x - величина зовнішнього кута, тоді за умовою маємо:
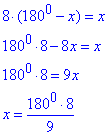
звідси x=1600.
Використаємо формулу для обчислення внутрішнього кута опуклого правильного многокутника (n-кутника):
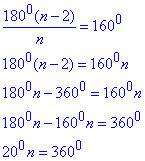
звідси n=18 вершин.
Відповідь: Г.
Приклад 33.21 Установити відповідність між кількістю кутів (1–4) многокутника та кількістю його діагоналей (А–Д).
1. 12 | А. 14 |
Розв'язування: Нехай n - кількість кутів (сторін, вершин) многокутника, тоді n(n-3)/2 - кількість діагоналей многокутника, отже маємо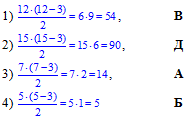 
Приклад 33.22 Установити відповідність між величиною внутрішнього кута (1–4) правильного многокутника та кількістю його сторін (А–Д).
1. 1560 | А. 9 |
Розв'язування: Нехай n - кількість кутів (сторін, вершин) многокутника.
Формула величини внутрішнього кута многокутника
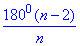
Застосовуємо її до кожного варіанту ЗНО тестів та знаходимо кількість сторін заданих многокутників.
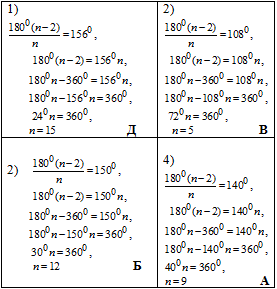
Приклад 33.23 Сторона правильного многокутника дорівнює 2 см.
Установити відповідність між кількістю сторін (1–4) цього многокутника та його площею (А–Д).
Розв'язування: Нехай n - кількість сторін (кутів, вершин) многокутника, a=2 см - довжина сторони правильного многокутника.
Площу правильного многокутника через кількість сторін знаходимо за формулою
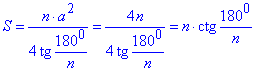
Виконуємо обчислення
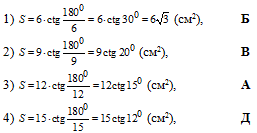
Приклад 33.24 Сума внутрішніх кутів многокутника удвічі більша від суми зовнішніх кутів, узятих по одному при кожній вершині. Знайти число сторін многокутника.
Розв'язування: Нехай n - кількість сторін многокутника, тоді 1800(n-2) - сума внутрішніх кутів многокутника,
3600 - сума зовнішніх кутів многокутника, узятих по одному при кожній вершині.
За умовою задачі маємо:
1800(n-2)=360•2,
n-2=4,
n=6.
Отже, заданий многокутник є шестикутником.
Відповідь: 6.
Приклад 33.25 Кожний із трьох внутрішніх кутів многокутника дорівнює 800, а кожний з решти кутів - 1500. Скільки найменше сторін може мати многокутник?
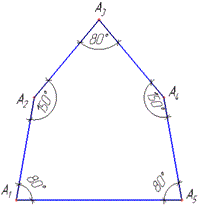Розв'язування: Нехай n - кількість сторін (кутів) многокутника. За умовою задачі кожний із трьох внутрішніх кутів заданого многокутника дорівнює 800 означає, що їх сума дорівнює
3•800=2400.
Кожний з решти внутрішніх кутів - 1500 означає, що їх сума дорівнює
(n-3)•1500.
Загальна сума всіх внутрішніх кутів (будь-якого) многокутника
(n-2)•1800.
Отже, маємо
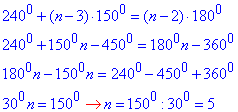
Отже, заданий многокутник є п'ятикутником.
Відповідь: 5.
Приклад 33.27 На скільки градусів збільшиться сума внутрішніх кутів многокутника, якщо число його сторін збільшити на 5?
Розв'язування: Нехай n - кількість сторін (вершин, кутів) многокутника,
тоді (n-2)•1800 - початкова сума внутрішніх кутів многокутника,
(n+5-2)•1800 - сума кутів многокутника, якщо число його сторін більше на 5 від початкового многокутника.
Порахуємо різницю початкової і кінцевої суми внутрішніх кутів многокутника:
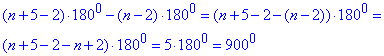
Отже, на 9000 збільшиться сума внутрішніх кутів многокутника, якщо число його сторін збільшити на 5.
Відповідь: 9000.
Приклад 33.28 Внутрішній кут правильного многокутника на 1440 більший від зовнішнього.
1) Знайти величину внутрішнього кута.
2) Скільки сторін має многокутник?
Розв'язування:
1) Внутрішній і зовнішній кути многокутника є суміжними кутами, тому разом у сумі мають 1800.
Нехай x - величина внутрішнього кута, тоді за умовою x-1440 - величина зовнішнього кута, тому внутрішній кут многокутника знаходимо з рівняння
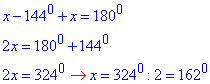
2) Нехай n - кількість сторін (кутів, вершин) многокутника,
тоді 1800(n-2)/n - величина внутрішнього кута многокутника, отже маємо
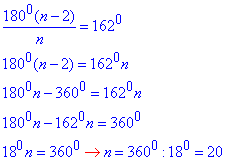
Заданий многокутник є двадцятикутником.
Відповідь: 1) 162; 2) 20.
Приклад 33.29 Радіус кола, описаного навколо правильного восьмикутника, дорівнює 4√2.
Знайти найменшу діагональ восьмикутника.
Розв'язування: Маємо правильний восьмикутник A1A2…A8, у якого R=4√2 - радіус описаного кола з центром O.
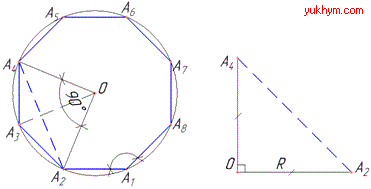Центральний кут многокутника (кут між двома сусідніми радіусами описаного кола):
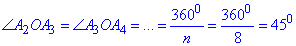
Найменша діагональ восьмикутника A2A4 відтинає рівнобедрений ΔA2A3A4 з кутом при вершині, що дорівнює подвоєному центральному куту (за властивістю), тобто ∠A2OA4.
Отже, розглянемо прямокутний рівнобедрений ΔA2OA4 (∠A2OA4=900), у якого A2O=A4O=R=4√2 - катети, A2A4=d - гіпотенуза.
За теоремою Піфагора знайдемо гіпотенузу – меншу діагональ правильного восьмикутника:
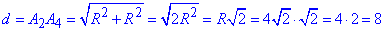
Відповідь: 8.
Приклад 33.32 Під яким кутом (у градусах) перетинаються дві діагоналі правильного п'ятикутника, проведені з різних вершин?
Розв'язування: Наведемо рисунок правильного п'ятикутника A1A2A3A4A5, у якого A1A3 і A2A4 - діагоналі, які перетинаються в точці B.
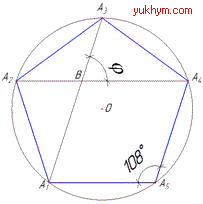
Обчислимо його внутрішній кут за формулою:
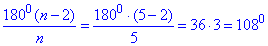
Опишемо коло навколо правильного п'ятикутника A1A2A3A4A5.
Отримали чотирикутники A1A2A4A5 і A1A3A4A5, які вписані у коло, тоді за властивістю суми їх протилежних кутів дорівнюють 1800.
Звідси, отримаємо у чотирикутника A1A2A4A5:
∠A1A5A4=∠A2A1A5=108 (як кути правильного п'ятикутника A1A2A3A4A5),
тоді ∠A1A2A4=∠A2A4A5=1800-1080=720 (як кути вписаного чотирикутника у коло).
Оскільки для чотирикутника A1A2A4A5 отримали ∠A1A5A4=∠A2A1A5=1080, ∠A1A2A4=∠A2A4A5=72 і ∠A1A5A4+∠A1A2A4=∠A5A1A5+∠A2A4A5=1800, то цей чотирикутник є рівнобічною трапецією A1A2A4A5 з основами A1A5 і A2A4, тому A2A4||A1A5.
Аналогічно встановлюємо, що чотирикутник A1A3A4A5 є рівнобічною трапецією з основами A1A3 і A4A5, тому A1A3||A4A5.
Звідки слідує, що чотирикутник BA1A5A4 - паралелограм (протилежні сторони паралельні), тому ∠A3BA4=∠BA1A5=∠A2A4A5=720 - кут між діагоналями A1A3 і A2A4.
Відповідь: 720.
Приклад 33.33За стороною a правильного дванадцятикутника визначити його апофему (перпендикуляр, опущений з центра до сторони), якщо a=2-√3.
Розв'язування: Апофема правильного многокутника є радіусом вписаного кола в цей многокутник. Використаємо формулу радіуса вписаного кола для правильного n-кутника:
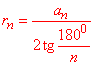де n - кількість сторін (кутів, вершин) правильного многокутника.
Для 12-кутника маємо (n=12 і a12=a):
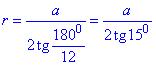
Для обчислення tg(150) використаємо формулу половинного аргументу:
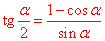При alpha=300 отримаємо
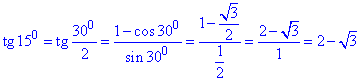
Знаходимо апофему (радіус вписаного кола) правильного дванадцятикутника за формулою
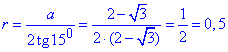
Відповідь: 0,5.
Приклад 33.34 Виразити сторону a правильного дванадцятикутника через радіус R описаного кола, й обчислити її довжину, якщо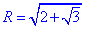 
Розв'язування: Використаємо формулу радіуса описаного кола для правильного n-кутника:
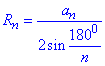
де n - кількість сторін (кутів, вершин) правильного многокутника.
Для 12-кутника маємо (n=12 і a12=a):
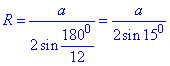
Звідси отримаємо, a=2R•sin(150).
Для обчислення sin(150) використаємо формулу половинного аргументу:
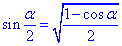
синус 150 рівний
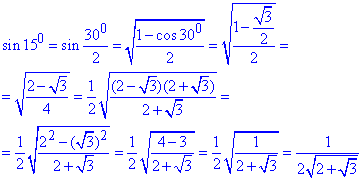
Значення навмисне розписували, щоб в подальших обчисленнях легко спростити при множенні на радіус R з умови.
Знаходимо довжину сторони правильного дванадцятикутника
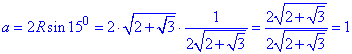
Ось такі розрахунки Ви повинні вміти виконувати на ЗНО тестах.
В 10, 11 класах подібні приклади зустрічаються рідше, але і їх обчислення вимагають відповідного рівня знань.
Відповідь: 1.
Приклад 33.35 На клумбі, яка має форму правильного восьмикутника зі стороною 1 м, потрібно посадити квіти. Скільки найбільше квітів можна посадити на такій клумбі, якщо для однієї рослини потрібно 160 см2 землі?
Розв'язування: Зробимо математичну модель задачі.
Позначимо клумбу як правильний восьмикутник, сторона якого a=1 м=100 см, тоді його площу обчислюємо за формулою:
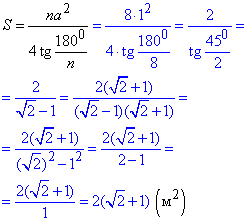
де тангенс 22,50 знайдемо із залежності
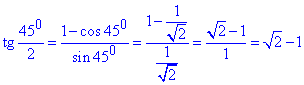
Оскільки для однієї рослини потрібно 160 см2, або 0,016 м2 землі, то їх кількість:
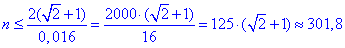
тобто n=301.
Отже, не більше 301 квітку можна посадити на такій клумбі, якщо для однієї рослини потрібно 160 см2 землі.
Відповідь: 301.
Далі Вас чекають задачі на шестикутники, які не увійшли до цієї та попередньої статті на многокутники.
