Продовжуємо розбирати готові відповіді із ЗНО тестів на геометричні перетворення графіків функцій: паралельне перенесення, симетричне відображення, розтяг та стиск. Щоб не повертатися до попередніх десяти прикладів та теорії нагадаємо основні геометричні перетворення з ескізами відповідних графіків.
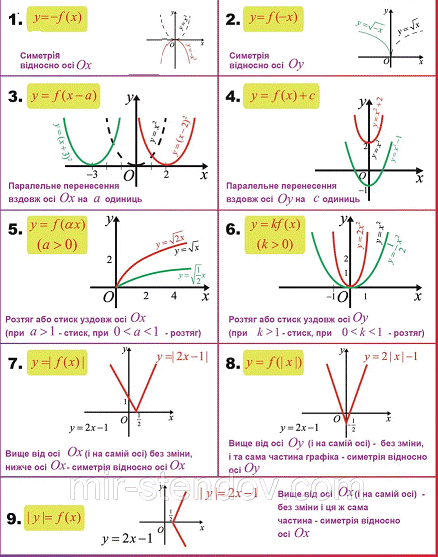
Таблицю можете завантажити та використовувати при розв'язуванні подібних завдань самостійно. А зараз перейдемо до розгляду тестових завдань із ЗНО підготовки з математики.
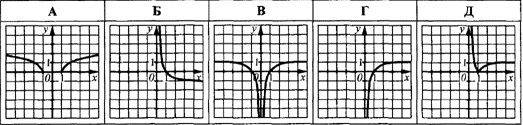
Приклад 23.11 На якому з рисунків зображено графік функції y=|log2x|?
Розв'язування: Графік функції y=|f(x)| можна одержати із графіка функції y=f(x) наступним чином: ту частину графіка функції y=f(x), яка розміщена над віссю Ox, у тому числі точки перетину графіка з віссю абсцис, залишаємо без змін, а ту частину, яка розміщена під віссю абсцис, симетрично відображаємо відносно цієї осі (Ox).
Побудуємо логарифмічну функцію, та її модуль за допомогою інструкції виписаної вище.
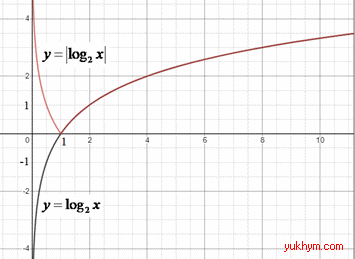
Відповідь: Д.
Приклад 23.12 На рисунку зображено графік функції y=f(x).
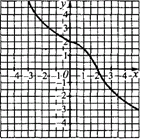
На якому з рисунків зображено графік функції y=f(|x|)?
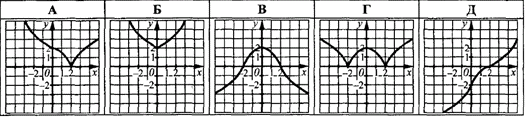
Розв'язування: Графік функції y=f(|x|) можна одержати із графіка функції y=f(x) наступним чином: ту частину графіка функції y=f(x), яка розміщена праворуч осі Oy, у тому числі точки перетину графіка з віссю ординат, залишаємо без змін, а ту частину, яка розміщена ліворуч від осі ординат (для від'ємних x), замінюємо симетричною до розташованої праворуч частини відносно осі ординат (Oy).
Із запропонованих тестових відповідей варіант В задовільняє правило.
Відповідь: В.
Приклад 23.13 Графік функції y=x^3 зсунули ліворуч на 4 одиниці й відобразили симетрично відносно осі Ox. Графік якої функції отримали в результаті таких перетворень?
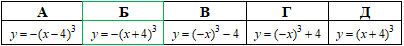
Розв'язування: Щоб отримати графік функції y=(x+4)3 необхідно графік y=x3 зсунути ліворуч на 4 одиниці.
Графік функції y=(x+4)^3 відобразили симетрично відносно осі Ox, отримаємо y=-(x+4)^3.
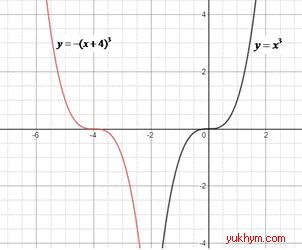
Відповідь: y=-(x+4)^3 – Б.
Приклад 23.14 Областю значень функції y=f(x) є проміжок [-2;2].
Знайти область значень функції y=4f(x)-3.
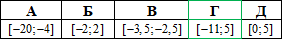
Розв'язування: Будьте уважними та прослідкуйте як змінюється область визначення та область значень при геометричних перетвореннях графіків функцій.
Оскільки функцію y=4f(x)-3 отримують з функції y=f(x) розтягом останньої у 4 рази до осі Ox та зсуненням на 3 одиниці вниз (відносно осі Oy), то запишемо як мінятиметься область значень при цьому
-2≤f(x)≤2,
-2•4≤4•f(x)≤2•4, тобто -8≤4•f(x)≤8,
-8-3≤4•f(x)-3≤8-3, тобто -11≤4•f(x)-3≤5.
Знайшли E(y)=[-11;5] - область значень функції y=4f(x)-3.
Відповідь: [-11;5] – Г.
Приклад 23.15 У результаті яких послідовних перетворень із графіка функції y=f(x) можна отримати графік функції y=f(2x+6)?

Розв'язування: З графіка функції y=f(x) отримали графік функції y=f(2x) в результаті стиснення удвічі до осі Oy. З графіка функції y=f(2x) отримали графік функції y=f(2(x+3)) в результаті паралельного перенесення на 3 одиниці вліво (відносно осі Ox). Отримали y=f(2x+6).
Відповідь: В.
Приклад 23.16 Областю визначення функції y=f(x) є проміжок [0;2]. Знайти область визначення функції y=f(x/2-4).
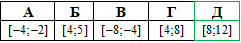
Розв'язування: Функцію y=f(x/2-4) отримують з функції y=f(x) паралельним перенесенням на 4 одиниці вправо та розтягом удвічі від осі Oy. Виконаємо послідовно перетворення
D1(y)=[4;6] - область визначення функції y=f(x-4) (область визначення зсунули на 4 одиниці).
D(y)=[8;12] - область визначення функції y=f(x/2-4) (область визначення розширили удвічі від попередньої).
Отримали варіант Д тестових відповідей.
Відповідь: [8;12] – Д.
Приклад 23.17 Ескіз графіка якої з наведених функцій зображено на рисунку?
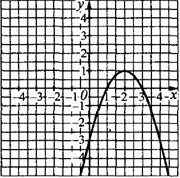
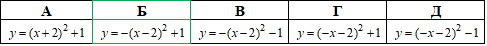
Розв'язування: Візьмемо функцію y=-x^2 (параболу з гілками вниз і вершиною в початку координат, точка (0;0)).
На заданому ескізі графіка вершина параболи знаходиться у точці (2;1), отже графік функції y=-x^2 паралельно перенесли на 2 одиниці вправо (вздовж осі Ox) і на 1 одиницю вгору (вздовж осі Oy).
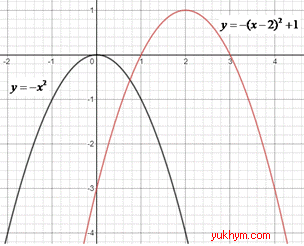
Отримали графік функції y=-(x-2)2+1.
Слідкуйте за тим як змінюються рівняння функцій при відповідних зміщеннях.
Відповідь: y=-(x-2)^2+1 – Б.
Приклад 23.18 Ескіз графіка якої з наведених функцій зображено на рисунку?
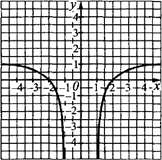
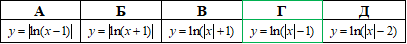
Розв'язування: Оскільки в відповідях фігурують логарифми, то за елементарну функцію над якою будемо виконуватимемо перетворення візьмемо логарифм y=ln(x) (логарифмічна крива, яка перетинає вісь Ox в точці (1;0)).
На заданому ескізі графіка логарифмічна крива перетинає вісь Ox в точці (2;0) і симетрично відображена відносно осі Oy, отже отримаємо паралельне перенесення графіка на 1 одиницю вправо і модуль абсциси x, тобто y=ln(|x|-1).
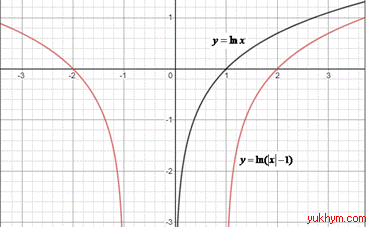
Відповідь: y=ln(|x|-1) – Г.
З наведених прикладів Ви повинні навчитися будувати ескізи графіків функцій за допомогою простих геометричних перетворень, а також за ескізами графіків бачити які дії потрібно виконати, щоб з елементарних функцій прийти до заданого графіка функції.
Попереду Вас чекає біля десятка готових відповідей з підготовки до ЗНО тестів на перетворення графіків функцій.


