Приклади на обернені та складені функції. ЗНО підготовка

Продовжуємо розбирати готові відповіді із ЗНО підготовки на властивості елементарних функцій і сьогодні проаналізуємо готові відповіді на обернені та складні функції, та все що з тим пов'язано. Багато з наведених відповідей Вам допоможуть при тестуванні та навчанні у ВУЗах, тому основні моменти та схеми розрахунків розбирайте самостійно.

Розділ 22. Елементарні функції та їх властивості

Обернені функції

Приклад 22.22 Вказати функцію, обернену до функції y=4x-1.

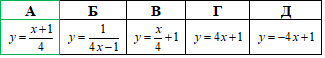
Розв'язування: У заданій функції y=4x-1 змінимо місцями y і x, запишемо x=4y-1.
З останньої рівності виразимо y – це і буде обернена функція до заданої:
-4y=-x-1,
y=(-x-1)/(-4), або y=(x+1)/4.
Відповідь: y=(x+1)/4 – А.

Приклад 22.23 Вказати функцію, обернену до функції y=x²-2, x∈[0;+ ∞).

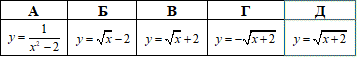
Розв'язування: Оскільки x∈[0;+ ∞), то y∈[-2;+ ∞).
У заданій функції y=x²-2 змінимо місцями y і x, запишемо x=y²-2 (звідси y∈[0;+ ∞) і x ∈[-2;+ ∞)). З останньої рівності виразимо y – це і буде обернена функція до заданої:
x=y²-2,
-y²=-x-2,
y²=x+2, або .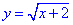
ОДЗ кореневої функції: x ∈[-2;+ ∞), як і має бути, отже обернена функція 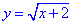існує!
Відповідь: 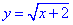– Д.

Приклад 22.35 Установити відповідність між функціями (1–4) та оберненими до них функціями (А–Д).

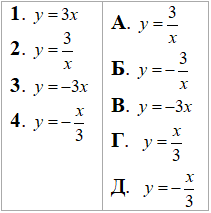
Розв'язування: Детальне пояснення як будувати обернені функції до заданих дивись у 22.22.
1. y=3x, заміна: x=3y, звідси y=x/3 1 - Г.
2. y=3/x, заміна: x=3/y, звідси y=3/x 2 - А.
3. y=-3x, заміна: x=-3y, звідси y=-x/3 3 - Д.
4. y=-x/3, заміна: x=-y/3, звідси y=-3x 4 - В.

Складні функції. Дослідження функцій

Приклад 22.24 Вказати складену функцію y=f(g(x)), якщо g(x)=1/x, f(x)=1/(x²+1).

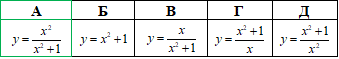
Розв'язування: Щоб отримати складну функцію y=f(g(x)) потрібно у функції 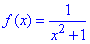замінити x на вираз g(x)=1/x (тобто у функції 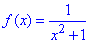«незалежною змінною» буде функція g(x)=1/x, де x ≠0), отже

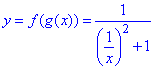
спростимо вираз:
.
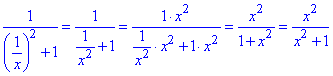Остаточно .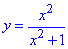, це відповідає варіанту А тестів ЗНО.

Відповідь: – А.

Приклад 22.25 Вказати складену функцію y=f(g(x)), якщо 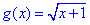, f(x)=x²-1.

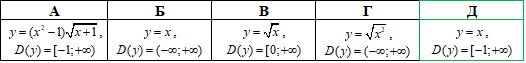
Розв'язування: Щоб отримати складену функцію y=f(g(x)) потрібно у функції f(x)=x²-1 замінити x на вираз 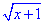(тобто у функції f(x)=x²-1 «незалежною змінною» буде функція 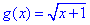, де 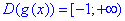), отже 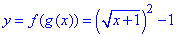, спростимо вираз: .
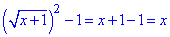Остаточно y=x, причому D(y)=[-1;+ ∞)..
Відповідь: y=x, D(y)=[-1;+ ∞) – Д.

Приклад 22.26 Знайти множину значень функції y=5^sin(x).

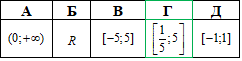
Розв'язування: Розглянемо функцію z=sin(x). Її найменше значення z_min=-1, а найбільше z_max=1 (за властивістю функції синуса z=sin(x)).

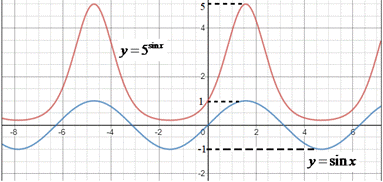
Функція y=5^z зростаюча, тому, підставивши найменше і найбільше значення функції синус в останню рівність, отримаємо найменше і найбільше значення заданої функції, відповідно:

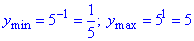
Запишемо множину значень заданої функції:
E(y)=[1/5;5].
Відповідь: [1/5;5] – Г.

Приклад 22.27 На рисунку зображено графік функції y=f(x), яка визначена на відрізку [-4;6]. Скільки всього коренів має рівняння f(x)=x на цьому відрізку?

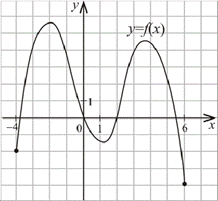
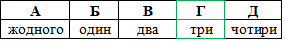
Розв'язування: Проведемо додатково пряму y=x.

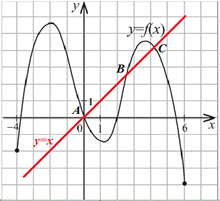
Знайдемо такі точки, у яких графіки функцій y=f(x) та y=x перетинаються, тобто знайдемо розв'язки рівняння f(x)=x:
це точки A, B і C (всього три корені).
Не думайте домальовувати ліву вітку кривої і будувати, ще одну точку. Це неправильно + в умові чітко вказано, що функція визначена на проміжку [-4;6], все решта нас не цікавить.
Будьте уважними з такого типу завданнями.
Відповідь: три – Г.

Приклад 22.28 Знайти множину значень функції y=1/(1+x²).

Розв'язування: Розглянемо функцію z=1+x².

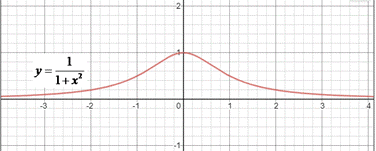
Вона зростає і є парною на всій області визначення, тому її найменше значення z_min=1 (при x=0), а найбільшого не існує (тобто є нескінченно великим числом, z_max→∞).
Функція y=1/z - обернена пропорційність, тому y_max=1 (при z_min=1).
Найменшого значення не існує, але так як z_max→∞, то y_min→0 (самого 0 так і не досягне).
Запишемо множину значень заданої функції:
E(y)=(0;1].
Відповідь: (0;1] – В.

Приклад 22.29 Знайти найбільше ціле значення функції .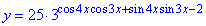

Розв'язування: Спростимо вираз cos(4x)cos(3x)+sin(4x)sin(3x):
cos(4x)cos(3x)+sin(4x)sin(3x)=cos(4x-3x)=co(x).
1) Розглянемо функцію y₁=cos(x).

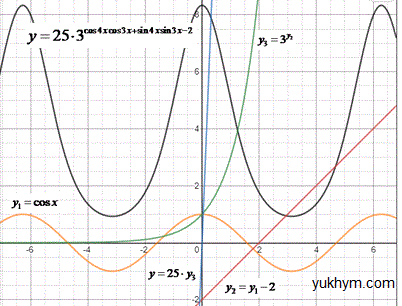
Її найменше значення y_1min=-1, а найбільше y_1max=1 (за властивістю функції косинуса y₁=cos(x)). (На рис. жовтий колір).
2) Розглянемо функцію y₂=y₁-2.
Її найменше значення y_2min=-3, а найбільше y_2max=-1 (за властивістю лінійної зростаючої функції на деякому проміжку). (На рис. червоний колір).
3) Розглянемо функцію y₃=3^y₂.
Її найменше значення (на деякому проміжку) 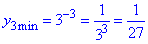, а найбільше 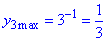(за властивістю показникової функції, як зростаючої на всій області визначення). (На рис. зелений колір).
3) Розглянемо функцію y=25•y₃.
Її найменше значення 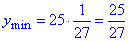, а найбільше 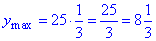(за властивістю лінійної зростаючої функції на проміжку). (На рис. синій колір).
Запишемо множину значень заданої функції:
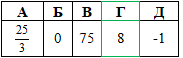
E(y)=[25/27;25/3].
Отже, число 8 є найбільшим цілим значенням функції .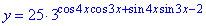
Відповідь: 8– Г.

Приклад 22.41 Знайти область визначення функції.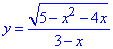
У відповідь записати кількість цілих значень аргументу в області визначення.
Розв'язування: Для заданої складеної дробово ірраціональної функції виписуємо дві умови на область визначення:
1) підкоренева функція не повинна приймати від'ємних значень;
2) знаменник дробової функції не повинен дорівнювати нулю.
Розв'язуємо систему нерівностей для знаходження ОДЗ:

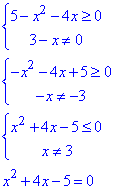
за теоремою Вієта отримаємо два корені квадратного рівняння
x₁=-5, x₂=1.
Наносимо розв'язки на числову вісь і, методом підстановки точки, встановлюмо знаки квадратного тричлена на інтервалах.

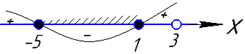
Отже, x∈[-5;1].
Запишемо усі цілі значення аргументу в області визначення:
-5; -4; -3; -2; -1; 0; 1.
Усього 7 цілих розв'язків.
Відповідь: 7.

Попереду Вас чекає багато готових прикладів із ЗНО підготовки, тому залишайтеся з нами та діліться посиланням на ресурс з друзями. Поступово разом пройдем всі типи завдань, що можуть чекати Вас на тестуваннях та при практичних у навчанні.