ЗНО 2019 математика. Відповіді, повні розв'язки №24-33

Продовжуємо аналіз готових відповідей ЗНО 2019 року з математики. Пояснення до тестових завдань достатньо добре розписані та графічно оформлені, тому Вам легко буде розібратися, що і для чого виконували.

Завдання 24. На рисунку зображено куб ABCDA1B1C1D1. Установіть відповідність між парою прямих (1– 4) та їх взаємним розташуванням (А–Д).

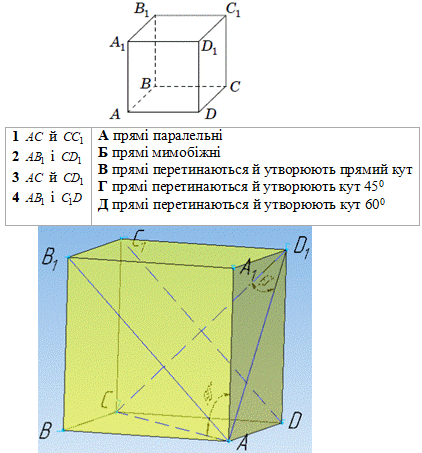
Розв'язування: 1. Пряма CC1 перпендикулярна до площини основи (квадрата ABCD), тому вона перпендикулярна до кожної прямої, що лежить у цій площині, AC⊥CC1 тобто прямі AC й CC1 перетинаються й утворюють прямий кут. В
2. Прямі AB1 і CD1 лежать у різних площинах і не перетинаються, тому прямі AB1 і CD1 мимобіжні. Б
3. Прямі AC й CD1 є діагоналями граней куба. У куба усі грані рівні, а тому діагоналі кожної грані також рівні, тому разом з діагоналлю AD1 утворюють рівносторонній ΔACD1, у якого всі сторони рівні, а також всі кути рівні і дорівнюють 60⁰. Отже, прямі AC й CD1 перетинаються й утворюють кут 60⁰. Д.
4. Прямі AB1 і C1D лежать в одній площині (діагональний переріз AB1C1D) і не перетинаються, тому прямі AB1 і C1D паралельні (AB1||C1D). А.

Завдання 25. У таблиці наведено тарифи на доставку вантажу за маршрутом N службою кур'єрської доставки. Будь-яку кількість вантажів можна об'єднувати в один, маса якого дорівнює сумі мас об'єднаних вантажів. Жодних додаткових платежів за об'єднання вантажів чи доставку вантажу, окрім указаних у таблиці, немає.

1. За яку найменшу суму грошей P (у грн) можна доставити цією службою за
маршрутом N три вантажі, маси яких становлять 31 кг, 36 кг та 40 кг?
2. Скільки відсотків становить P від загальної суми грошей за доставку цих
трьох вантажів, якщо кожен з них відправляти окремо?
Розв'язування: 1. За доставку вантажу масою 31 кг - плата 100 грн, 36 кг - плата 100 грн, 40 кг - плата - 100 грн.
Разом 300 грн.
Порахуємо суми мас окремо і дізнаємось вартість її доставки:
31+36=67 кг - плата 110 грн;
31+40=71 кг - плата 110 грн;
36+40=76 кг - плата 205 грн;
31+31+40=107 - плата 310 грн (що є більшою, ніж за кожний вантаж окремо). Отже, якщо доставляти вантажі 31 кг і 36 кг (разом 67 кг), об'єднавши в один, і вантаж масою 40 кг окремо, то отримаємо: p=110+100=210 грн - найменша сума грошей, за яку можна доставити цією службою за маршрутом N три вантажі.
2. звідси

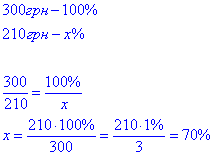
70% становить P від загальної суми грошей за доставку цих трьох вантажів, якщо кожен з них відправляти окремо.
Відповідь: 210; 70.

  Завдання 26. Розв'язування На рисунку зображено ромб ABCD, діагоналі якого перетинаються в точці O. Із цієї точки до сторони AD проведено перпендикуляр OK довжиною 3 см. Площа трикутника AOD дорівнює 15 см².

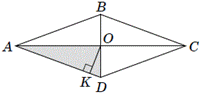
1. Визначте довжину сторони ромба ABCD (у см).
2. Обчисліть тангенс гострого кута ромба ABCD.

 Завдання 27. Обчислення За якого від'ємного значення x значення виразів x^2-4,3-5x та 2-3x будуть послідовними членами арифметичної прогресії?

Завдання 28. Маршрутний автобус, рухаючись зі сталою швидкістю, подолав відстань від міста A до міста B за 5 год, а на зворотний шлях витратив на 30 хв менше. Визначте швидкість (у км/год) автобуса на маршруті від A до B, якщо вона на 8 км/год менша за швидкість на маршруті від B до A. Уважайте, що довжини маршрутів від A до B та від B до A, якими рухався маршрутний автобус, рівні.
Розв'язування:Позначимо x, км/год - швидкість автобуса на маршруті від A до B;
x+8, км/год - швидкість автобуса на маршруті від B до A;
5x, км - відстань, довжина маршруту від A до B;
30 хв=0,5 год, тоді
5-0,5=4,5 год.
4,5(x+8), км - відстань, довжина маршруту від B до A.
За умовою довжини маршрутів від A до B та від B до A, якими рухався маршрутний автобус, рівні, тому
5x=4,5(x+8),
5x=4,5x+36,
(5-4,5)x=36,
0,5x=36,
x=36:0,5=72.
Шукана швидкість автобуса на маршруті рівна 72 км/год.
Відповідь: 72.

Завдання 29. У фінал пісенного конкурсу вийшло 4 солісти та 3 гурти. Порядковий номер виступу фіналістів визначають жеребкуванням. Скільки всього є варіантів послідовностей виступів фіналістів, якщо спочатку виступатимуть гурти, а після них - солісти? Уважайте, що кожен фіналіст виступатиме у фіналі лише один раз.
Розв'язування: Нехай m=4 - кількість солістів у фіналі;
n=3 - кількість гуртів у фіналі. Порахуємо кількість розташувань солістів у порядку їх виступу:
m!=4!=4·3·2·1=24.
Порахуємо кількість розташувань гуртів у порядку їх виступу:
n!=4!=3·2·1=6.
Тоді кількість варіантів послідовностей виступів фіналістів, якщо спочатку виступатимуть гурти, а після них - солісти обчислюють наступним чином: m!·n!=24·6=144.
Відповідь: 144.

Завдання 30. У прямокутній системі координат на площині xy задано прямокутний трикутник ACB (∠C=90). Коло з центром у точці A, задане рівнянням (x+3)^2+y^2-4y=21, проходить через вершину C. Сторона AC паралельна осі y, довжина сторони BC втричі більша за довжину сторони AC. Визначте координати вершини B(x_B;y_B), якщо вона лежить у першій координатній чверті. У відповідь запишіть суму x_B+y_B.

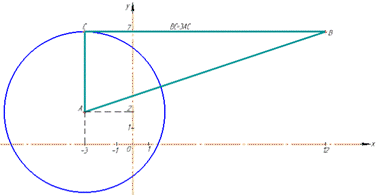
Розв'язування: Щоб визначити координати центра A(x_A;y_A) кола та його радіус R, зведемо задане рівняння кола до канонічного виду:

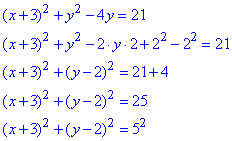
Кінцева формула описує коло з центром у точці A(-3;2) і радіусом R=5.
AC паралельна осі y (за умовою), то абсциса точки C дорівнює абсцисі точки A, тобто x_C=-3.
Обчислимо ординату точки C з умови, що ∠C=90⁰, тобто AC⊥BC і точка B(x_B;y_B) лежить у першій координатній чверті (за умовою), тобто BC паралельна осі x, тоді
|y_C-y_A|=R,
y_C-2=5,
y_C=5+2=7.
Координати C(-3;7).
Так як сторона BC паралельна осі x, то ордината точки B дорівнює ординаті точки C, тобто y_B=7.
Обчислимо абсцису точки B з умови, що BC=3·AC, тобто
BC=3R=3·5=15
і точка B(x_B;y_B) лежить у першій координатній чверті, тоді
|x_B-x_C|=15,  
x_B-(-3)=15,
x_B=15+(-3)=12.
Отож, отримали точку B(12;7),  де     x_B+y_B=12+7=19.
Відповідь: 19.

Завдання 31. Задано функції f(x)=2/x і g(x)=5-8x.
1. Побудуйте графік функції f.
2. Побудуйте графік функції g.
3. Знайдіть похідну функції f.
4. До графіка функції f проведено дотичні, паралельні графіку функції g. Визначте абсциси точок дотику.
Розв'язування: 1. Графік функції f(x)=2/x є гіпербола, гілки якої знаходяться в І та ІІІ чверті.
ОДЗ: x≠0.
Для побудови графіка знайдемо координати деяких точок і запишемо у таблицю:


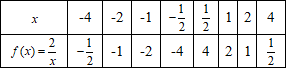
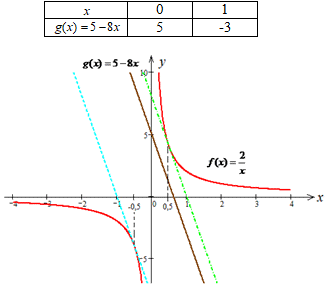
2. Графіком функції g(x)=5-8x є пряма. Для побудови прямої достатньо знайти координати двох точок, запишемо їх у таблицю.
Далі виконуємо побудову графіків функцій

3. Знайдемо похідну функції f(x)=2/x:

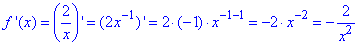
4. Знайдемо абсциси точок дотику x₀.
Запишемо рівняння дотичної:

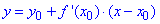
Оскільки дотичні до графіка функції f(x)=2/x є паралельними до прямої g(x)=5-8x (за умовою), то k=f'(x0)=-8 - кутовий коефіцієнт нахилу.
Звідси, F'(x0)=-8, тобто

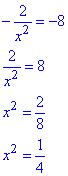
x₁=1/2 або x₂=-1/2;
x₁=0,5 або x₂=-0,5 - абсциси точок дотику дотичних до графіка функції f(x)=2/x, які паралельні до прямої g(x)=5-8x.

 Завдання 32. Обчислення та побудова У нижній основі циліндра проведено хорду AB, довжина якої дорівнює c. Цю хорду видно із центра верхньої основи під кутом α. Через хорду AB проведено площину β паралельно осі циліндра на відстані d (d≠0) від неї.
1. Зобразіть переріз циліндра площиною β та вкажіть його вид.
2. Обґрунтуйте відстань d.
3. Визначте площу цього перерізу.

Завдання 33. Задано систему нерівностей

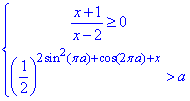
де x - змінна, a - стала.
1. Розв'яжіть першу нерівність цієї системи.
2. Визначте множину розв'язків другої нерівності системи залежно від значень параметра a.
3. Визначте всі розв'язки системи залежно від значень a.
Розв'язування: 1. Розв'яжемо першу нерівність системи:


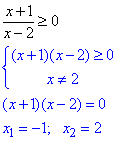
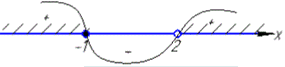
отже x∈(-∞;-1]∪(2;+∞).

2. Розв'яжемо другу нерівність системи залежно від значень a:

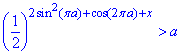
Спростимо вираз в показнику :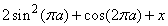

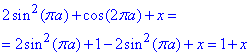
Тоді отримаємо


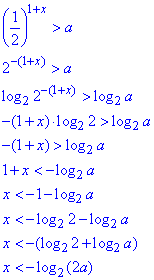
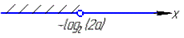
Якщо a∈(-∞;0], то x∈(-∞;+∞),
якщо a∈(0;∞), то x∈(-∞;-log₂(2a)).

3. Знайдемо множину всіх розв'язків заданої системи залежно від значень параметра a:

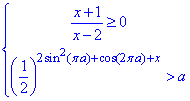
Запишемо спільні розв'язки обох нерівностей системи, отриманих у 1 і 2 попередніх пунктах, залежно від значення a.
Випадок І: a∈(-∞;0], тоді x∈(-∞;-1]∪(2;+∞).
Оскільки ця множина x є частиною множини (підмножиною) x∈(-∞;+∞). Випадок ІІ: a∈(0;∞), отримаємо

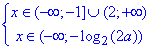
Знайдемо такі значення a, при яких

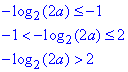
причому a>0:

Враховуючи отримані значення a для кожного випадку, запишемо множину всіх розв'язків заданої системи нерівностей:
якщо a∈(-∞;0], то x∈(-∞;-1]∪(2;+∞);
якщо a∈(0;1/8), то x∈(-∞;-1]∪(-∞;-log₂(2a));
якщо a∈[1/8;1), то x∈(-∞;-1];
якщо a∈[1;+∞), то x∈(-∞;-log₂(2a)).

Нагадуємо, що на сторінках сайту розжовані усі розділи зі Збірника тестових завдань з математики А. Капіносова, від Вас потрібна сила волі їх пройти та взяти для самоосвіти максимум корисної інформації.