ЗНО 2019 математика. Відповіді, повні розв'язки №1-23

Пропонуємо разом проаналізувати повні відповіді тесту ЗНО з математики за 2019 рік. Розв'язки достатньо компактні, щоб весь тест вмістився у дві статті. Уважно переглядайте та перевіряйте, чи у Вас такий самий хід розрахунків.

Завдання 1. Спростіть вираз 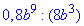, де b≠0.

Відповідь: 0,1b⁶ – А.

Завдання 2. Кола із центрами в точках O та O1 мають внутрішній дотик (див. рисунок). Обчисліть відстань OO1, якщо радіуси кіл дорівнюють 12 см і 8 см.

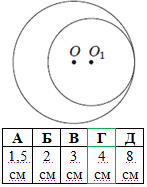
Розв'язування: Маємо коло з центром у точці O і радіусом r=12 см, а також коло з центром у точці O1 та радіусом r1=8 см.
Оскільки обидва кола мають зовнішній дотик, то
OO1=r-r1=12-8=4 см.
Відповідь: 4 см – Г.

Завдання 3. Розв'яжіть рівняння (x+1)(2x-3)=0.

Розв'язування: (x+1)(2x-3)=0,
x+1=0 або 2x-3=0, 2x=3,
звідси x1=-1 або x2=1,5.
Відповідь: -1; 1,5 – Д.

Завдання 4. Якщо ціна паркету (p) пов'язана із ціною деревини для його виробництва (d) співвідношенням p=5d+8, то d= ?

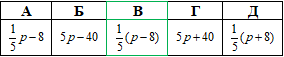
Розв'язування: p=5d+8,
p-8=5d,
d=(p-8)/5.
Відповідь: (p-8)/5 – В.

Завдання 5. Розгортку якого з наведених многогранників зображено на рисунку?

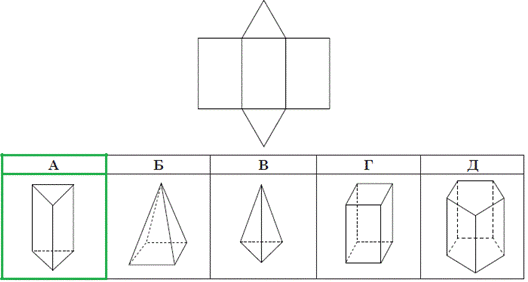
Розв'язування: На рисунку зображено розгортку прямої трикутної призми, у якої основи - два трикутники, а бічні грані - три прямокутники.
Відповідь: А.

Завдання 6. Укажіть формулу для обчислення об'єму V конуса, площа основи якого дорівнює S, а висота - h.

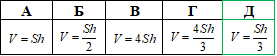
 Розв'язування: Об'єм V конуса дорівнює третині добутку площі основи S на висоту h, тобто

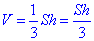
Відповідь: – Д.

Завдання 7. На рисунку зображено графік функції y=f(x), визначеної на проміжку [1;8]. Скільки нулів має ця функція на заданому проміжку?

Розв'язування: Нулі функції - це точки перетину графіка функції y=f(x) з віссю абсцис (Ox). Графік заданої функції y=f(x) перетинає вісь абсцис в одній точці, тому має один нуль функції.
Відповідь: один – Б.

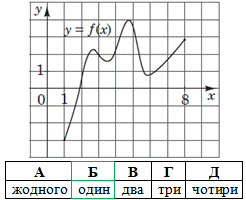
Завдання 8. Яке з наведених чисел є розв'язком нерівності |x|>3?

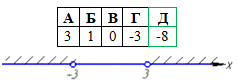
Розв'язування:

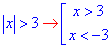
звідси x∈(-∞;-3)∪(3;+∞).
Цьому проміжку належить число -8.
Відповідь: -8 – Д.

Завдання 9. Яку з наведених властивостей має функція y=√x?
А   набуває лише невід'ємних значень
Б   спадає на всій області визначення
В  парна
Г  періодична
Д  має дві точки екстремуму

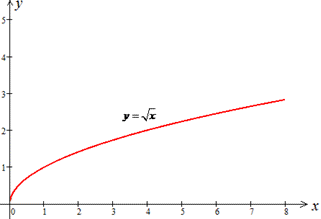
Розв'язування: За властивістю кореневої функції y=√x вона набуває лише невід'ємних значень (тобто y≥0);
зростає на всій області визначення;
не є парною, ні непарною;
неперіодична;
точок екстремуму не має.
Відповідь: набуває лише невід'ємних значень – А.

Завдання 10. Спростіть вираз (1-sin²α)•tg²α.

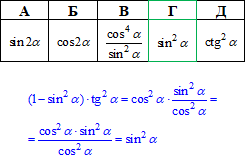
Відповідь: sin²α – Г.

Завдання 11. На діаграмі відображено розподіл кількості працівників фірми за віком. Скільки всього працівників працює на цій фірмі?

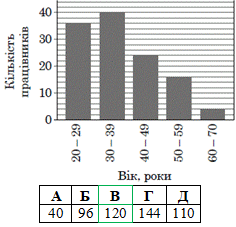
Розв'язування: Випишемо і додамо кількість працівників по кожному стовпчику на діаграмі:
36+40+24+16+4=120.
Відповідь: 120 – В.

Завдання 12. Скоротіть дріб


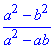
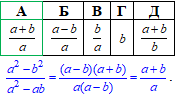
Відповідь: (a+b)/a – А.

Завдання 13. На рисунку зображено паралелограм ABCD. Які з наведених тверджень є правильними?

І. ∠ABC+∠BCD=180⁰.
ІІ. AB=CD.
ІІІ. AC⊥BD

Розв'язування: У паралелограма ABCD сума двох сусідніх кутів дорівнює 180⁰, тобто ∠ABC+∠BCD=180⁰;
протилежні сторони рівні, зокрема AB+CD;
діагоналі у точці перетину діляться навпіл, але не є перпендикулярними (у загальному випадку).
Відповідь: лише І і ІІ – В.

Завдання 14. Якому з наведених проміжків належить число log₂(1/3)?

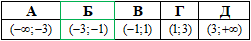
Розв'язування: Зробимо деякі перетворення:

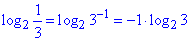
Графік функції y=log₂x зростає на всій області визначення (x>0),

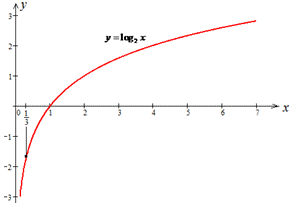
тому log₂2<log₂3<log₂4, де
log₂2=1 і

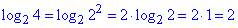
отже 1<log₂3<2, тоді
-2<-log₂3<-1,

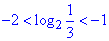
Тому (-3;-1) проміжок, якому належить число log₂(1/3).
Відповідь: (-3;-1) – Б.

Завдання 15. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-3;3].

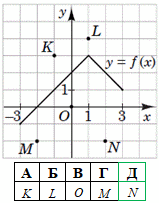
Одна з наведених точок належить графіку функції y=-f(x). Укажіть цю точку.
Розв'язування: Побудуємо графік функції y=-f(x), визначеної на проміжку [-3;3]. Точки графіка функції y=-f(x) є симетричними відносно осі абсцис (Ox) до точок графіка функції y=f(x).

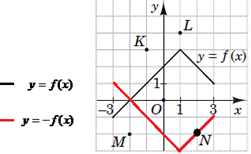
Точка з координатами (2;2), яка належить графіку функції y=f(x), є симетричною до точки N(2;-2) відносно осі абсцис, тому точка N належить графіку функції y=-f(x) (дивись рисунок).
Відповідь: N – Д.

Завдання 16. Розв'яжіть систему рівнянь

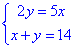
Для одержаного розв'язку укажіть (x0;y0) укажіть добуток x0•y0.

Розв'язування:

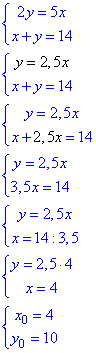
Отже, (4;10) - розв'язок системи рівнянь, тоді
x₀•y₀=4•10=40.
Відповідь: 40 – Г.

Завдання 17. Сторона основи правильної чотирикутної піраміди дорівнює 6 см, усі її бічні грані нахилені до площини основи під кутом 60⁰. Визначте площу бічної поверхні цієї піраміди.

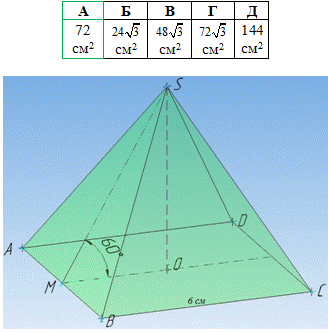
Розв'язування: Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD зі стороною 6 см.
Тоді площа основи піраміди (квадрата):
S_oc=S_ABCD=6^2=36 см².
За теоремою «про площу ортогональної проекції многокутника» маємо співвідношення:
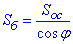, де S_б - площа бічної поверхні піраміди і φ=60⁰ – кут між бічною гранню і основою піраміди, двогранний кут при основі. 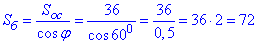см².
Відповідь: 72 см² – А.

Завдання 18. На рисунку зображено графіки функцій y=f(x) і y=g(x). Укажіть формулу для обчислення площі зафарбованої фігури.

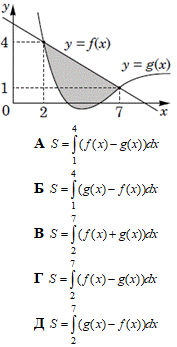
Розв'язування: При 2≤x≤7 маємо f(x)≥g(x), так як на графіку функція y=f(x) знаходиться вище, ніж функція y=g(x) на проміжку 2≤x≤7.
Тому площа зафарбованої фігури обчислюється наступним чином: .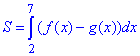
Відповідь: – Г.

Завдання 19. На кресленні кутової шафи (вид зверху) зображено рівні прямокутники ABCD і KMEF та п'ятикутник EMOAD (див. рисунок).

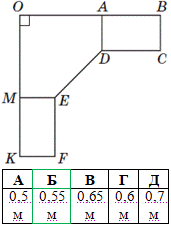
Визначте довжину відрізка ED, якщо OK=OB=1,2 м, KM=AB=0,5 м, KF=0,3 м. Укажіть відповідь, найближчу до точної.
Розв'язування: Зробимо математичну модель задачі.

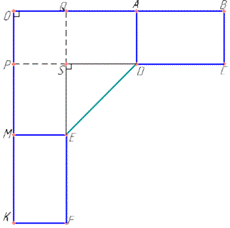
Маємо рівні прямокутники ABCD і KMEF та п'ятикутник EMOAD, у яких OK=OB=1,2 м, KM=AB=0,5 м, KF=BC=0,3 м.
З точки D на сторону OK і з точки E на сторону OB, відповідно, опустимо перпендикуляри DP та EQ, які перетнуться у точці S. Тоді отримаємо рівні прямокутники PMES і AQSD;
квадрат OQSP і прямокутний трикутник SED (∠DSE=90⁰). Отримаємо наступні розміри:
SE=PM=OK-KM-BC=1,2-0,5-0,3=0,4 (м);
SD=AQ=OB-AB-KF=1,2-0,5-0,3=0,4 (м).
У прямокутному трикутнику SED (∠DSE=90⁰), у якого SE=SD=0,4 м - катети, знайдемо гіпотенузу ED за теоремою Піфагора:

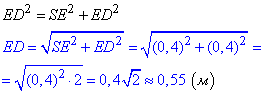
Відповідь: 0,55 м – Б.

Завдання 20. Якому з наведених проміжків належить корінь рівняння ?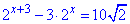

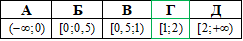
Розв'язування: Розкриємо показникове рівняння:

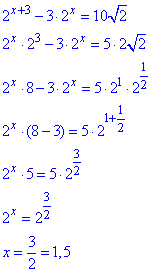
Отриманий корінь x=1,5 належить проміжку [1;2).
Відповідь: [1;2) – Г.

Завдання 21. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження.

Розв'язування: Побудуємо графіки заданих функцій.

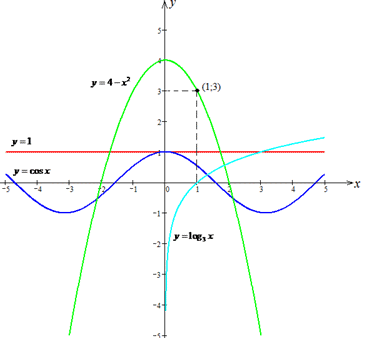
1. Графік функції y=1 є паралельним до осі абсцис (осі x), тому не має спільних точок з віссю x. Г
2. y=cos(x). Нехай y=0, тоді cos(x)=0, звідси

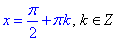
тому графік функції y=cos(x) має безліч спільних точок з віссю x. В
3. y(x)=4-x^2, тоді y(1)=4-1^2=3, отримали точку (1;3), отже графік функції y=4-x^2 проходить через точку (1;3). Д
4. y=log₃x. ОДЗ: x>0, отже графік функції y=log₃x не перетинає вісь y (ординат). А

Завдання 22. Установіть відповідність між твердженням про дріб (1– 4) та дробом, для якого це твердження є правильним (А–Д).

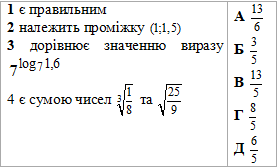
Розв'язування: 1 Дріб 3/5 є правильним, бо 3<5 Б.
2 6/5=1,2, тому належить проміжку (1;1,5) Д.
3 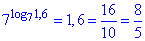Г.
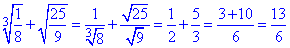4 А.

Завдання 23. Прямокутну трапецію ABCD (AD||BC, AD>BC) з більшою бічною стороною CD=10 описано навколо кола радіуса 4.

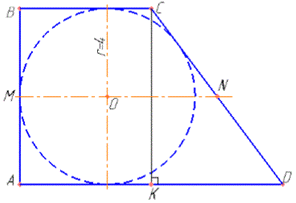
Установіть відповідність між величинами (1–4) та її числовим значенням (А–Д).

Розв'язування: 1. У прямокутній трапеції, в якій вписано коло, довжини меншої бічної сторони, висоти та діаметру кола рівні, тобто
AB=CK=2r=2•4=8, де AB||CK.
Отже, AB=8 - довжина сторони AB. Б.
2. У трапеції ABCD проведемо висоту CK до сторони AD (CK⊥AD). Відрізок KD - проекція сторони CD на пряму AD. У прямокутному ΔCKD (∠CKD=90), у якого CD=10 - гіпотенуза і CK=8 - катет, за теоремою Піфагора знайдемо інший катет KD:
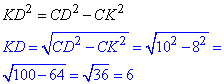А.
3. Якщо у чотирикутник (у трапецію ABCD) вписано коло, то суми протилежних сторін рівні, тобто BC+AD=AB+CD.
Нехай BC=x, тоді AD=AK+KD=x+6, так як AK=BC.
x+x+6=8+10,
2x=18-6=12,
x=6.
Отже, BC=6 і AD=6+6=12 - довжина сторони AD. Г
4. Відрізок MN - середня лінія трапеції ABCD.
Знайдемо її довжину:
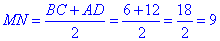В.

В наступній статті розглянемо наступні повні відповіді ЗНО 2019 тесту з математики.