Сьогодні проаналізувати повні відповіді ЗНО тесту з математики за 2018 рік. Пояснень мінімум, основні формули виписані та на методиках обчислень наголошено. Вам залишається перевірити, чи такий самий хід розразунків Ви зможете повторити на реальних тестах.
Завдання 1. 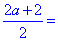
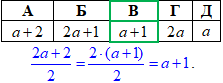
Відповідь: a+1 – В.
Завдання 2. Три прямі, розміщені в одній площині, перетинаються в одній точці (див. рисунок). Визначте градусну міру кута α.
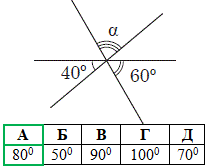
Розв'язування: Тут потрібно використати властивість,що ∠AOB=1800 - розгорнутий кут має 180 градусів.
∠AOM=400, ∠BON=600, тоді ∠AOB=AOM+∠MON+∠BON, звідси
∠MON=∠AOB-(∠AOM+∠BON)=1800-(400+600)=800.
Кути α і ∠MON вертикальні, тому α=∠MON=800.
Відповідь: 800 – А.
Завдання 3. У буфеті друзі купили кілька однакових тістечок вартістю 10 грн кожне і 5 однакових булочок вартістю x грн кожна. Яке з чисел виражає загальну вартість цієї покупки (у грн), якщо x - ціле число?
А | Б | В | Г | Д |
31 | 32 | 33 | 34 | 35 |
Розв'язування: Введемо позначення до задачі.
Нехай y - кількість однакових тістечок, x - вартість однієї булочки.
Тоді
y•10+5•x=5(2y+x).
Отримане ціле число є кратним 5, тому має ділитися на 5 націло і закінчуватися цифрою 0 або 5.
Таким числом із запропонованих в тесті є 35.
Відповідь: 35 – Д.
Завдання 4. На рисунку зображено графік функції y=f(x), визначеної на проміжку [-4;6]. Укажіть найбільше значення функції f на цьому проміжку.
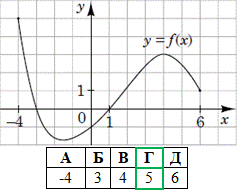
Розв'язування: Досить простий приклад, головне не сплутати з локальним максимумом.
З рисунку бачимо, що
ymax=y(-4)=5 - найбільше значення функції на зображеному проміжку.
Відповідь: 5 – Г.
Завдання 5. Яке з наведених чисел є коренем рівняння log4(x-1)=3?
А | Б | В | Г | Д |
4 | 13 | 63 | 65 | 82 |
Розв'язування: Спершу випишемо ОДЗ: x-1>0, x>1.
Якщо рівняння складне то на тестах ОДЗ не розписують, а після обчислень розв'язки перевіряємо на правильність підстановкою. Це щодо того, як зекономити час на ЗНО тестах.
Далі розкриємо логарифмічне рівняння, скориставшись властивістю, що логарифм основи рівний одиниці
log4(x-1)=3log44,
log4(x-1)=log443,
log4(x-1)=log464,
x-1=64,
x=64+1=65.
Відповідь: 65 – Г.
Завдання 6. Укажіть формулу для обчислення об'єму V півкулі радіуса R (див. рисунок).
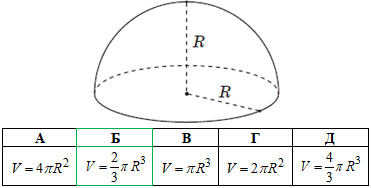
Розв'язування: Тут потрібно знати формулу об'єму кулі радіуса R:
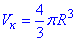
Тоді об'єм півкулі:
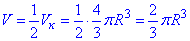
Відповідь: V=2/3·πR3– Б.
Завдання 7. Розв'яжіть рівняння 4√x=1.
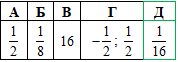
ОДЗ кореневої функції:
x≥0
Підносимо до квадрату обидві частини, щоб позбутися кореня, та розписуємо
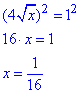
Відповідь: 1/16 – Д.
Завдання 8. Знайдіть область визначення функції
y=(x+1)/(x-2)
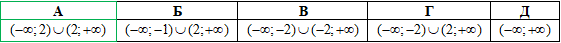
Розв'язування:Випишемо область допустимих значень для дробової функції
 .
.
ОДЗ: x-2≠0, x≠2, звідси x∈(-∞;2)∪(2;+∞).
Відповідь: x∈(-∞;2)∪(2;+∞) – А.
Завдання 9. У просторі задано паралельні прямі m і n. Які з наведених тверджень є правильними?
А | Б | В | Г | Д |
лише І | лише ІІ | лише ІІ та ІІІ | лише ІІІ | лише І та ІІ |
Розв'язування: Через дві паралельні прямі m і n у просторі можна провести площину, в цій же площині можна провести пряму, що перетинає прямі m і n (тобто твердження І та ІІ правильні). Але не існує такої точки, що належить обом прямим m і n, оскільки паралельні прямі не перетинаються (твердження ІІІ хибне).
Відповідь: лише І та ІІ – Д.
Завдання 10. Спростіть вираз 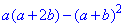
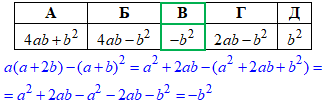
Відповідь: -b2 – В.
Завдання 11. На рисунку зображено паралельні прямі a і b та січну CD. Знайдіть відстань між прямими a і b, якщо CK=5 см, KD=2 см, а відстань від точки K до прямої a дорівнює 1 см.
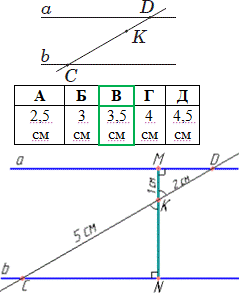
Розв'язування: Відстань між паралельними прямими a і b - це спільний перпендикуляр проведений до цих прямих.
Проведемо перпендикуляр MN так, щоб точка K належала цьому перпендикуляру.
a||b, MN⊥a, MN⊥b, MN=MK+KN,
де MK=1см - відстань від точки K до прямої a(MK⊥a);
CK=5 см, KD=2 см.
Розглянемо прямокутні трикутники DMK (∠DMK=90) і CNK (∠CNK=90), у яких кути при вершині K рівні як вертикальні.
Звідси випливає, що ці трикутники подібні, а тому їх відповідні сторони пропорційні, тобто
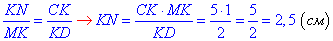
Знайдемо довжину відрізка MN - відстань між паралельними прямими a і b:
MN=MK+KN=1+2,5=3,5 (см).
Відповідь: 3,5 см – В.
Завдання 12. Учень з понеділка до п'ятниці записував час (у хвилинах), який він витрачав на дорогу до школи та зі школи (див. таблицю).
На скільки хвилин у середньому дорога зі школи триваліша за дорогу до школи?
А | Б | В | Г | Д |
2 | 3 | 4 | 5 | 6 |
Розв'язування: Обчислимо середню тривалість дороги до школи (загальну кількість хвилин (їх суму) за всі робочі дні поділимо на кількість цих днів, тобто на 5):
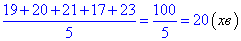
Обчислимо середню тривалість дороги зі школи (загальну кількість хвилин (їх суму) за всі робочі дні поділимо на кількість цих днів, тобто на 5): 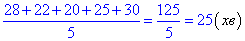
Визначимо на скільки хвилин у середньому дорога зі школи триваліша за дорогу до школи:
25-20=5 (хв).
Відповідь: 5 – Г.
Завдання 13. 1-sin(a)ctg(a)cos(a)=

Відповідь: sin2(a) – Д.
Завдання 14. Розв'яжіть систему рівнянь
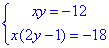
Якщо (x0;y0) - розв'язок системи, то x0=
А | Б | В | Г | Д |
-6 | -16 | -9 | 2 | 6 |
Розв'язування:Спростимо систему рівнянь
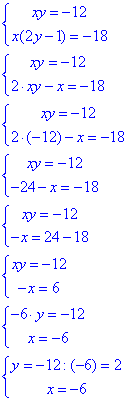
(-6;2) - розв'язок системи рівнянь, тому x0=-6.
Відповідь: -6 – А.
Завдання 15. На рисунку зображено розгортку правильної трикутної призми. Визначте площу бічної поверхні цієї призми, якщо периметр розгортки (суцільна лінія) дорівнює 52 см, а периметр основи призми становить 12 см.
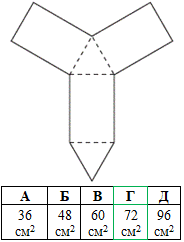
Розв'язування: Площа бічної поверхні прямої призми:
Sb=Poc•H, де Poc=12 см - периметр основи призми, з іншої сторони
Poc=3a - периметр основи правильної трикутної призми, у якої a - сторона основи, тобто
a=Poc:3=12:3=4 см;
H - висота призми.
Знайдемо її. За умовою задачі:
P=52 см - периметр розгортки призми (суцільна ліня), яка складається з 4 ребер основ і 6 бічних ребер призми, тобто
P=4a+6H, тоді
4•4+6H=52,
6H=52-16=36,
H=36:6=6 см.
- Висота правильної трикутної призми рівна H=6 см.
Тоді її площа
Sb=Poc•H=12•6=72 (см2).
Відповідь: 72 см2 – Г.
Завдання 16. Обчисліть значення виразу log345+log3900-log3500.

Відповідь: 4 – Б.
Завдання 17. На рисунку зображено фрагмент графіка періодичної функції з періодом T=2π, яка визначена на множині дійсних чисел. Укажіть серед наведених точку, що належить цьому графіку.
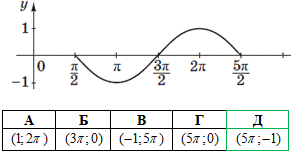
Розв'язування: З фрагменту графіка функції видно, що точка (-π;1) належить графіку, тобто f(π)=-1.
Враховуючи період T=2π і його властивість періодичної функції f(x+k•T)=f(x), отримаємо
f(5π)=f(π+2•2π)=f(π)=-1.
Тому точка (5π;-1) також належить заданому графіку.
Відповідь: (5π;-1) – Д.
Завдання 18. Обчислення Розв'яжіть нерівність 2x+22x+3≥144
Завдання 19. Укажіть похідну функції f(x)=x(x^3+1).
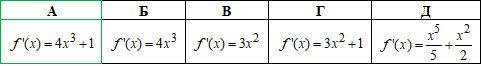
Розв'язування: Маємо f(x)=x(x^3+1)=x^4+x - функція.
Тоді її похідна f(x)=4x^3+1.
Відповідь: f(x)=4x^3+1 – А.
Завдання під номерами №20-33 можете переглянути та самостійно розібрати з наступної публікації.


