Повні відповіді ЗНО 2018 математика. №20-33

Продовжуємо розбирати готові відповіді ЗНО 2018 року з математики.

Завдання 20. На рисунку зображено фрагмент поперечного перерізу стіни (прямокутник KLMN) з арковим прорізом ABFCD, верхня частина BFC якого є дугою кола радіуса 1 м. Відрізки AB і DC перпендикулярні до AD, AB=DC=2 м. AD=1,6 м, KL=2,75 м. Визначте відстань d від найвищої точки F прорізу до стелі LM.

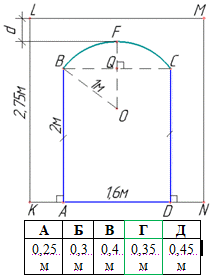
Розв'язування: Зробимо математичну модель задачі. Маємо дугу BFC кола радіусом 1м (за умовою), тоді OB=OF=1 м (як радіуси кола). Далі маємо AD=BC=1,6 м, тоді BQ=QC=C:2=0,8 м.
У прямокутному ΔBQO (∠BQO=90) знайдемо катет OQ:

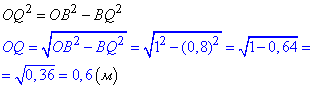
Тоді FQ=OF-OQ=1-0,6=0,4 (м).
Довжина відрізка KL=2,75 м:
KL=AB+FQ+d, звідси отримаємо
d=KL-AB-FQ=2,75-2-0,4=0,35 (м).
Відповідь: 0,35м – Г.

Завдання 21. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження.

Розв'язування: Побудуємо графіки заданих функцій:
y=4,5x; y=-4; y=2x+4; y=x; y=2x; y=x^2-1; y=3^x і проаналізуємо їх розташування.

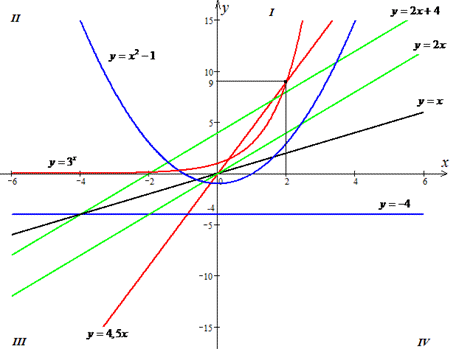
1. Пряма y=4,5x перетинає графік функції y=3^x у точці з абсцисою x₀=2, бо y(2)=4,5•2=9 і y(2)=3₂=9 (червоний колір). В

2. Пряма y=-4 не має спільних точок з графіком функції y=x²-1, (на рисунку позначені синім кольором). Б

3. Пряма y=2x+4 є паралельною прямій y=2x (зелений колір), бо k₁=k₂=2, де y=k•x+b - рівняння прямої. А

4. Пряма y=x є бісектрисою І і ІІІ координатних чвертей (чорний колір). Д

Завдання 22. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження, якщо a=-3.

Розв'язування: 1. a⁰=1 для будь-якого a≠0. Значення виразу a^0 дорівнює 1. Б

2. a²¹, якщо a=-3.
Якщо a=-3, то значення виразу a² більше за 1. А

3. 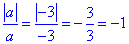, якщо a=-3.
Якщо a=-3, то значення виразу |a|/a дорівнює -1. Г

4.
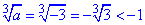
Якщо a=-3, то корінь кубічнй з відємного числа -3 менший за -1. Д

Повні відповіді до наступних тестів Ви можете переглянути за посиланнями перед умовою завдання. 

Завдання 23. Обчислення Циліндр і конус мають рівні об'єми та рівні радіуси основ. Площа основи циліндра дорівнює 25π см2, а його об'єм - 100π см3. До кожного початку речення (1–4) доберіть його закінчення (А–Д) ...

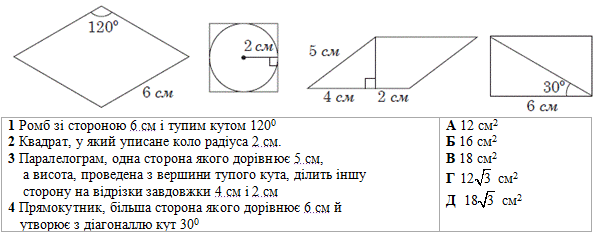
Завдання 24. Повна відповідь Установіть відповідність між геометричною фігурою (1– 4) та її площею (А–Д).

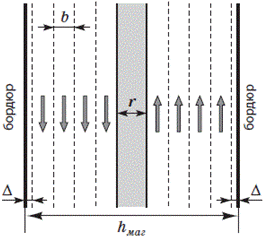
Завдання 25. Для визначення ширини автомагістралі hмаг (у м), що має по 4 однакові смуги руху транспорту в обох напрямках (див. рисунок), використовують формул
у hмаг=8b+r+2Δ де b - ширина однієї смуги руху транспорту;
r - ширина розділювальної смуги між напрямками руху транспорту;
Δ - ширина запобіжної смуги між крайньою смугою й бордюром.

1. Визначте ширину b (у м) однієї смуги, якщо hмаг=40,2 м, r=10 м, Δ=1,5 м.
2. Заплановано збільшити ширину b кожної смуги руху транспорту на 10% за рахунок лише зменшення ширини r розділювальної смуги. На скільки метрів потрібно зменшити ширину r розділювальної смуги?
Розв'язування: 1. За умовою завдання маємо:
hмаг=8b+r+2Δ, тоді обчислимо

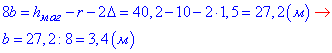
ширина однієї смуги =3,4м.
2. Складемо пропорцію та розпишемо

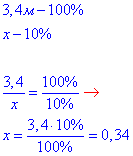
b1=b+0,34=3,4+0,34=3,74 м - збільшена на 10% ширина однієї смуги.
Обчислимо зменшену ширину r1 розділювальної смуги:

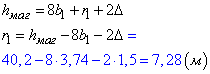
Визначимо, на скільки метрів потрібно зменшити ширину r розділювальної смуги:
r-r1=10-7,28=2,72 (м).
Відповідь: 3,4; 2,72.

Завдання 26. Відповідь У прямокутному трикутнику ABC (∠C=90) відстані від середини медіани BM до катетів AC і BC дорівнюють 5 см і 6 см відповідно.
1. Визначте довжину катета AC (у см).
2. Визначте радіус (у см) кола, описаного навколо трикутника ABC.

Завдання 27. Пояснення Знаменник геометричної прогресії дорівнює 2/3, а сума чотирьох перших її членів дорівнює 65. Знайдіть перший член прогресії.

Завдання 28. У майстерні мали виготовити 240 стільців за n днів, причому щодня планували виробляти однакову кількість стільців. Однак, на прохання замовника, завдання виконали на 2 дні раніше запланованого терміну. Для цього довелося денну норму виготовлення збільшити на 4 стільці. Визначте n.
Розв'язування: Позначимо вхідні величини:
n - запланована кількість днів;
n-2 - фактична кількість днів;
240/n - запланована денна норма;
240/(n-2) - запланована денна норма;
ОДЗ: n>0, n≠2 (n- натуральне число).

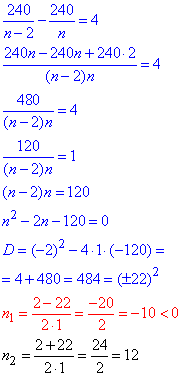
З розрахунків n=12 - запланована кількість днів.
Відповідь: 12.

Завдання 29. В Оленки є 8 різних фотографій з її зображенням та 6 різних фотографій її класу. Скільки всього в неї є способів вибрати з них 3 фотографії зі своїм зображенням для персональної сторінки в соціальній мережі та 2 фотографії свого класу для сайту школи?
Розв'язування: Порахуємо кількість способів вибрати 3 фотографії з 8 зі своїм зображенням:

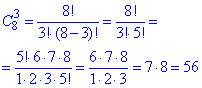
Порахуємо кількість способів вибрати 2 фотографії з 6 її класу:

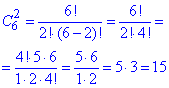
Загальна кількість способів вибрати усі фотографії:

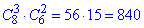
Відповідь: 840.

Завдання 30. Відповідь У прямокутній системі координат на площині задано колінеарні вектори 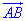та 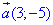. Визначте абсцису точки B, якщо A(-4;1), а точка B лежить на прямій y=3.

Завдання 31. Обчислення Задано функції f(x)=x^3 і g(x)=4|x|.
1. Побудуйте графік функції f.
2. Побудуйте графік функції g.
3. Визначте абсциси точок перетину графіків функцій f і g.
4. Обчисліть площу фігури, обмеженої графіками функцій f і g.

Завдання 32. Відповіді У правильній чотирикутній піраміді ...
1. Побудуйте переріз піраміди SABCD площиною β.
2. Обґрунтуйте вид перерізу.
3. Визначте периметр перерізуї.

Завдання 33. Розв'яжіть нерівність 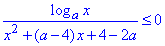залежно від значень параметра a.
Розв'язування: Почнемо аналіз з ОДЗ знаменника дробу та логарифма:

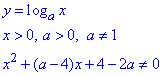
Нерівність заміняємо еквівалентною системою:

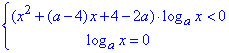
Розв'яжемо квадратне рівняння:

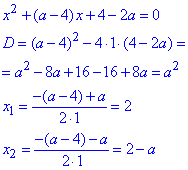
Квадратний тричлен x²+(a-4)x+4-2a запишемо у вигляді:
x²+(a-4)x+4-2a=(x-2)(x-2+a).
Розв'яжемо задану нерівність методом інтервалів.
Причому врахуємо знак логарифма з такими параметрами (дивись графік функції y=logax):
при 0<a<1 і 0<x<1 маємо log_ax>0;
при 0<a<1 і x>1 маємо log_ax<0;
при a>1 і 0<x<1 маємо log_ax<0;
при a>1 і x>1 маємо log_ax>0.

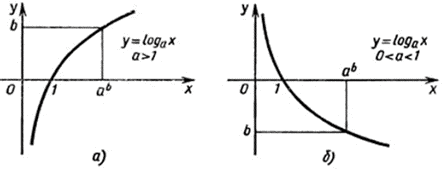
Тому нерівність

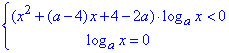
справелива при наступній комбінації параметрів та "ікс":
a∈(0;1) маємо x∈[1;2-a)∪(2;+∞),
при a∈(1;21) отримаємо x∈[0;2-a)∪[1;2),
при a∈(2;+∞) маємо x∈[1;2).

Вважаємо, що розібрані приклади в повній мірі сприятимуть Вашій підготовці до вступу у ВУЗи. Подібні завдання до тем ЗНО тесту Ви можете знайти на сторінках сайту, усі розділи зі Збірника тестових завдань з математики А. Капіносова нами розв'язані, тому від Вас лише потрібне бажання навчитися!