Основні формули для обчислення площі паралелограма наведені нижче
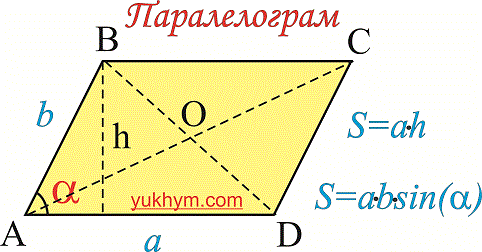
Якщо є бажання, можете переглянути властивості паралелограма, ознаки та все що з ним пов'язано. Далі наведені відповіді до завдань із ЗНО підготовки на знаходження площі паралелограма, периметра, виведення формул.
Знаходження площі паралелограма. ЗНО тести
Приклад 32.32 Висоти паралелограма дорівнюють 4 і 6, а його периметр – 40. Знайти площу і гострий кут (у градусах) паралелограма.
Розв'язування: Побудуємо паралелограм ABCD, у якого протилежні сторони паралельні AB||CD і AD||BC, PABCD=40 - периметр.
BM=4 - висота, що проведена до сторони AD (BM⊥AD);
BK=6 - висота, що проведена до сторони CD (BK⊥CD) за умовою.
Рисунок паралелограма із заданими висотами наведено нижче
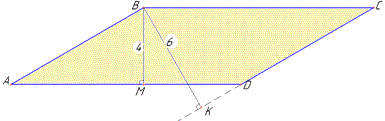
Запишемо формули для обчислення площі паралелограма ABCD:
SABCD=BM•AD=BK•CD, звідси 4AD=6CD, або AD=1,5CD.
З формули для обчислення периметра паралелограма ABCD:
PABCD=2•(CD+AD), знаходимо сторони
2•(CD+AD)=40,
2•(CD+1,5CD)=40,
5CD=40,
CD=40/5=8, звідси AB=CD=8.
Тоді сторона паралелограма рівна BC=AD=1,5•8=12.
Знайдемо площу паралелограма через добуток сторони на висоту, що до цієї сторони опущена:
SABCD=BM•AD=4•12=48.
У прямокутному трикутнику ΔABM (∠M=90) за означенням синуса гострого кута прямокутного трикутника знайдемо гострий ∠A – гострий кут паралелограма:
sin(∠A)=BM/AB=4/8=1/2.
Оскільки, sin(∠A)=1/2 звідси робимо висновок, що кут ∠A =30.
Відповідь: 48; 30.
Приклад 32.33 Одна сторона паралелограма на 2 більша за іншу, а його діагоналі дорівнюють 8 і 14. Знайти периметр паралелограма.
Розв'язування: Нехай маємо паралелограм ABCD, AB||CD і AD||BC;
AC=14, BD=8 - діагоналі паралелограма. Позначимо AB=CD=x, тоді за умовою BC=AD=x+2.
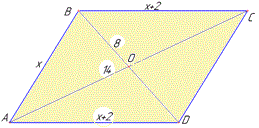
Розглянемо трикутник ΔBCD, у якого CD=x, DC=x+2 і BD=8, що лежить проти гострого кута ∠C. Тоді, за теоремою косинусів запишемо косинус кута ∠C:
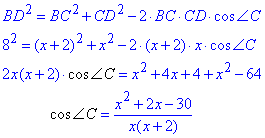
За властивістю кутів паралелограма ABCD маємо:
∠B+∠C=180, звідси ∠B=180-∠C.
Тоді cos(∠B)=cos(180-∠C)=-cos(∠C).
Розглянемо ΔABC, у якого AC=14, AB=x, BC=x+2,
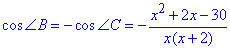
Тоді за теоремою косинусів складемо рівняння для знаходження невідомих сторін паралелограма:
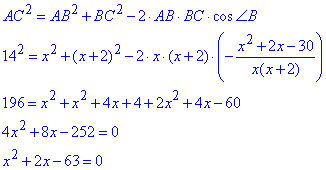
За теоремою Вієта отримаємо два корені квадратного рівняння:
x1=-9<0 і x2=7.
Звідси, AB=CD=7 і BC=AD=9.
Знайдемо периметр паралелограма ABCD:
PABCD=2•(CD+AD)=2•(7+9)=32.
Відповідь: 32.
ЗНО 2018. Завдання 24. Установіть відповідність між геометричною фігурою (1– 4) та її площею (А–Д).
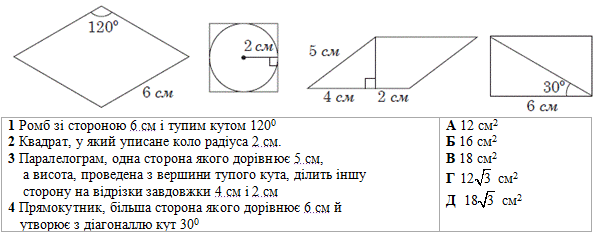
Розв'язування: 1. Маємо ромб ABCD, у якого всі сторони рівні: a=AB+BC=CD=AD=6 см і ∠B=120 (кут між сторонами AB і BC).
Тоді площа ромба ABCD:
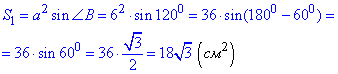
Д
2. Маємо квадрат ABCD, у якого вписане коло радіуса OM=2 см. За властивістю квадрата описаного навколо кола, обчислимо довжину сторони квадрата ABCD:
a=AD=OM•2=2•2=4 см .
Тоді площа квадрата ABCD:
S2=a^2=4^2=16 (см2). Б
3. Маємо паралелограм ABCD, у якого a=AD=AK+KD=4+2=6 см - довжина сторони.
Знайдемо висоту h=BK паралелограма (із прямокутного ΔABK, ∠AKB=90):

Тоді площа паралелограма ABCD:
S3=a•h=6•3=18 (см2). В
4. Маємо прямокутник ABCD, у якого a=AD=6 см - довжина однієї зі сторін. Знайдемо іншу сторону b=AB прямокутника (за означенням тангенса прямокутного ΔABD, ∠A=90, ∠ADB=30):
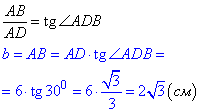
Тоді площа прямокутника ABCD:
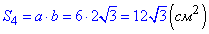 Г
Г
Приклад 32.36 Визначити: більшу сторону паралелограма; площу паралелограма за його висотами h1 і h2 та периметром P й обчислити їх значення, якщо h1=3, h2=7, P=20.
Розв'язування: Нехай маємо паралелограм ABCD, AB||CD, AD||BC, PABCD=P - периметр. Схематичний рисунок паралелограма до умови наведено нижче

BA'=h1 - висота, що проведена до сторони AD (BA'⊥AD);
BC'=h2 - висота, що проведена до сторони CD (BC'⊥CD) за умовою.
За властивістю паралелограма ABCD: AB=CD і AD=BC – довжини сторін паралелограма.
Запишемо вираз для обчислення периметра паралелограма ABCD:
PABCD=2•(AB+BC)=P.
Позначимо AB=CD=x, тоді 2•(x+BC)=P, x+BC=0,5P звідси BC=AD=0,5P-x.
Запишемо формули для обчислення площі паралелограма:
SABCD=BA'•AD=BC'•CD, звідси складаємо рівняння
h1•(0,5P-x)=h2•x, розпишемо та виразимо невідому x
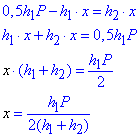
Можемо записати сторони AB, CD
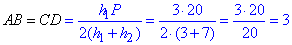 , (AB=h1=BA')
, (AB=h1=BA')
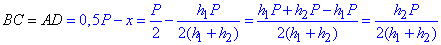
Підставляємо значення з умови в формули
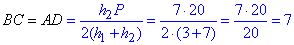 (BC=h2=BC') – більша сторона паралелограма (прямокутника) ABCD, оскільки BC=BC' і AB=AB'.
(BC=h2=BC') – більша сторона паралелограма (прямокутника) ABCD, оскільки BC=BC' і AB=AB'.
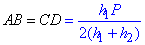
Обчислюємо площу паралелограма (прямокутника):
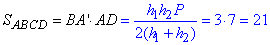
Відповідь: 7; 21.
Приклад 32.43 Знайти квадрат площі паралелограма, якщо його більша діагональ дорівнює 2√7, а висоти дорівнюють √3 і 2√3.
Розв'язування: Нехай маємо паралелограм ABCD, AB||CD і AD||BC, у якого AC=2√7 - більша діагональ, CK=√3 (BK⊥AD), BD=2√3 (BD⊥CD) - висоти.
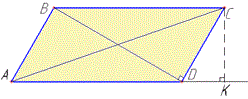
Запишемо формули для обчислення площі паралелограма ABCD:
SABCD=CK•AD=BD•CD, тобто √3AD=2√3CD, звідси AD=2CD.
Позначимо: AB=CD=x і BC=AD=2x - сторони паралелограма ABCD.
У прямокутному трикутнику ΔACK (∠K=90) за допомогою теореми Піфагора знайдемо катет AK:

У прямокутному ΔDCK (∠K=90) за теоремою Піфагора запишемо вираз:
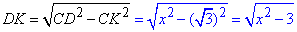
Запишемо довжину відрізка AK і знайдемо x:
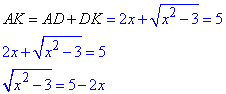
ОДЗ: 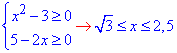
звідси
x^2-3=(5-2x)^2,
x^2-3=25-20x+4x^2,
3x^2-20x+28=0,
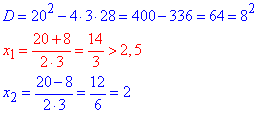
(не належить ОДЗ)
Отримали: AB=CD=2 і BC=AD=4 - сторони паралелограма ABCD.
Знайдемо площу паралелограма ABCD:
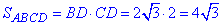
Запишемо квадрат площі паралелограма ABCD:
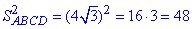
Відповідь: 48.
Приклад 32.45 Знайти площу паралелограма з точністю до 0,01 см^2, якщо його більша діагональ дорівнює 5, а висоти дорівнюють 2 і 3.
Розв'язування: Нехай маємо паралелограм ABCD, AB||CD і AD||BC, у якого AC=5 - більша діагональ, CK=2 (BK⊥AD), BD=3 (BD⊥CD) - висоти.

Запишемо формули для обчислення площі паралелограма ABCD:
SABCD=CK•AD=BD•CD, тобто 2AD=3CD, звідси AD=1,5CD.
Позначимо: AB=CD=x і BC=AD=1,5x - сторони паралелограма ABCD.
У прямокутному ΔACK (∠K=90) за теоремою Піфагора знайдемо катет AK:
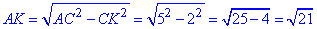
У прямокутному ΔDCK (∠K=90) за теоремою Піфагора запишемо вираз:
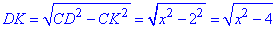
Запишемо довжину відрізка AK і знайдемо x:
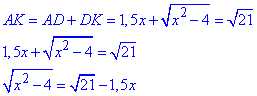
Випишемо ОДЗ на корені рівняння:
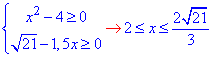
Позбуваємося коренів піднесенням до квадрата
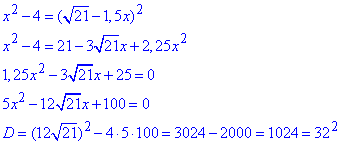
через дискримінант обчислюємо корені квадратного рівняння
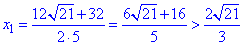 (не належить ОДЗ),
(не належить ОДЗ),
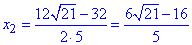
Отже отримали:
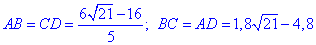 - сторони паралелограма ABCD.
- сторони паралелограма ABCD.
Знайдемо площу паралелограма ABCD з точністю 0,01:
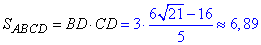
Відповідь: 6,89.
Вчіться розв'язувати важчі задачі на паралелограми, прості приклади зі шкільної програми навчать Вас хіба що добре виконувати рисунки та властивості паралелограма. На складних задачах Ви одночасно пригадуєте кілька розділів математики, тут Вам і трикутники, квадратні рівняння, теорема Піфагора, тригонометрія.


