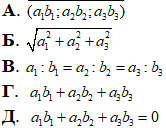Означення. Колінеарними називають вектори, які паралельні між собою або лежать на одній прямій.
Умова колінеарності:
- два вектори колінеарні якщо пропорційні їх координати
ax/bx=ay/by=az/bz. - вектори a(a1;a2;a3) і b(b1;b2;b3) колінеарні, якщо можна знайти таке число k, що виконується відношення
b=k•a: b1=k•a1; b2=k•a2; b3=k•a3.
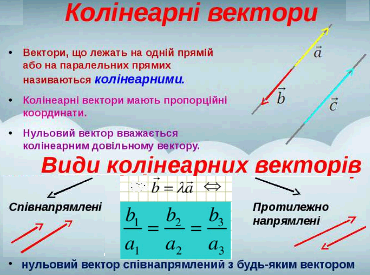
Основні властивості колінеарних (паралельних) векторів, які Ви повинні вивчити та знати, наведено на схемі
В 10,11 класі учні це вчать, ми тільки повторюємо матеріал та готуємо Вас до іспитів. Далі наведені готові розв'язки ЗНО тестів.
Для швидкого завантаження сторінок ми не ставили знак вектора, хоча при розв'язуванні потрібно. За правильний приймайте запис векторів, який фігурує у формулах.
Приклад 42.25 Установити відповідність між назвами формул для векторів a(a1;a2;a3) і b(b1;b2;b3) (1–4) та формулами (А – Д).
1. Довжина вектора |a| |
|
Розв'язування: У попередніх уроках всі ці формули використовувалися, тому просто випишемо їх:
1. Довжина вектора a:
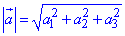Б.
2. Формула скалярного добутку векторів (a,b):
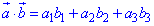Г.
3. Умова перпендикулярності векторів a⊥b:
a⊥b, якщо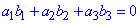 
Д.
4. Умова колінеарності векторів a||b:
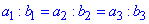В.
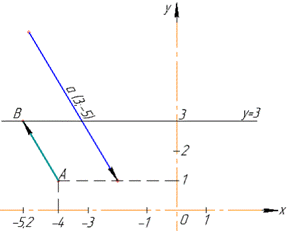
ЗНО 2018. Завдання 30. У прямокутній системі координат на площині задано колінеарні вектори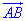 
та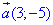 
. Визначте абсцису точки B, якщо A(-4;1), а точка B лежить на прямій y=3.
Розв'язування: Нехай маємо B(x;3), де x - абсциса точки B і 3 - ордината точки B, так як за умовою завдання точка B лежить на прямій y=3.
Запишемо координати вектора AB, у якого
A(-4;1): x-(-4)=x+4 - абсциса вектора ;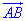
3-1=2 - ордината вектора 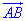, отже 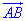(x+4;2). Оскільки за умовою задачі вектори 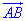(x+4;2) та a колінеарні, то їх відповідні координати пропорційні (за властивістю):
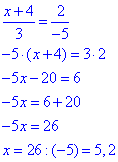
Отримали точку B(-5,2;3), де x=-5.2 абсциса точки B.
Відповідь: -5,2.
Приклад 42.7 Серед векторів a(4;14;2), b(2;7;-1), c(0;0;3), d(-6;-21;3) знайти колінеарні.
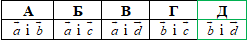
Розв'язування: Вектори колінеарні, якщо лежать на паралельних або на одній прямій. Якщо вектори колінеарні, то їх координати пропорційні!
Перевіримо колінеарність векторів a і b:
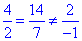
координати не пропорційні, отже вектори a і b не є колінеарними.
Перевіримо колінеарність векторів a і c:
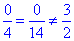
умова колінеарності не виконується, вектори a і c не є колінеарними.
Перевіримо колінеарність векторів a і d:
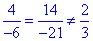
умова не виконується, вектори a і d не є колінеарними.
Перевіримо колінеарність векторів b і c:
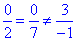звідси вектори b і c не є колінеарними.
Перевіримо колінеарність векторів b і d:
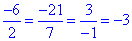
координати пропорційні, отже вектори b і d колінеарні.
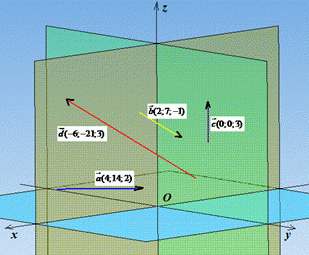
З рисунку до умови можна побачити, що лише вектори b і d паралельні. Коефіцієнт пропорційності -3 вказує на те, що вектори напрямлені в протилежну сторону і вектор d по довжині (модулю) втричі більший за вектор b.
Відповідь: b і d – Д.
Приклад 42.8 За якого значення параметра n вектори a(n+5;-8;n+1) і b(5;1-n;3) колінеарні.
А | Б | В | Г | Д |
±5 | ±5; 9 | -9 | 5 | 5; 9 |
Розв'язування: Якщо вектори колінеарні, то їх координати пропорційні, тобто для векторів a(ax;ay;az) і b(bx;by;bz) має виконуватися умова:
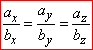
За умовою a(n+5;-8;n+1) і b(5;1-n;3) маємо
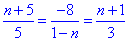
Розв’яжемо рівняння:
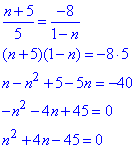
за теоремою Вієта отримаємо
n1=5, n2=-9.
Тепер перевіримо, чи отримані розв’язки задовольняють умову колінеарності з третьою координатою:
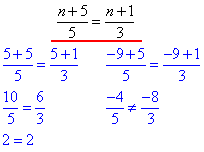
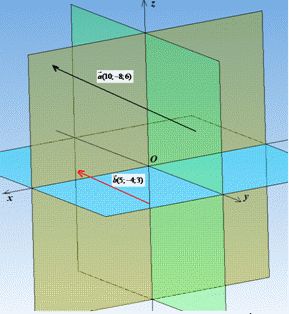
Робимо висновок, що при n=5 задані вектори a і b задовольняють умову 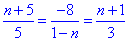, тому їх координати пропорційні, а самі вектори a(10;-8;6) і b(5;-4;3) колінеарні. На рисунку ці вектори є паралельними.
Відповідь: 5 – Г.
Приклад 42.36 Дано вектори a(-2;0), b(1;-1) і c(2;3).
За якого значення параметра k вектори 2a-k•b і c будуть колінеарними?
Розв'язування: Знайдемо координати вектора 2a-k•b:
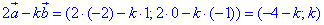
Вектори 2a-k•b і c колінеарні, якщо їх відповідні координати пропорційні:
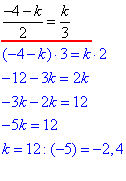
При k=-2,4 вектори 2a-k•b і c (тобто 2a-k•b=(-1,6;-2,4) і c(2;3)) будуть колінеарними.
Відповідь: -2,4.
Наведені приклади найбільш поширені, і в 10, 11 класі Ви їх проходили, принаймі мали розбирати. Попереду завдання на обчислення скалярного добутку векторів, обчислення кутів між векторами та розв'язування задач на суму та різницю векторів.
