Як обчислити площу плоскої фігури, що обмежена лініями?

Розберемо готові відповіді до прикладів на знаходження площі плоскої фігури, що обмежена кривими через подвійні інтеграли.
Завдання не складні, а вся схема знаходження площі вимагає всього трьох речей:
знання елементарних функцій та вміння шукати точки їх перетину;
розуміння як через криволінійні інтеграли шукати площу, вміння правильно розставляти межі;
добрих знань з обчислення інтегралів, оскільки до цього все зводиться.

Приклад 1. Знайти площу фігури, що обмежена лініями. Зробити малюнок.
y=cos(x), y=0, x=-π/2, x=π/6.
Обчислення: Запишемо межі інтегрування: π/2≤x≤π/6. 
Побудуємо косинусоїду та заштрихуємо поверхню, площу якої потрібно знайти.

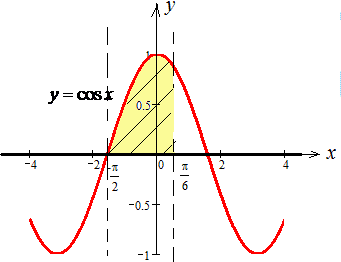
Через інтеграл обчислюємо площу фігури між y=0 s косинусом:

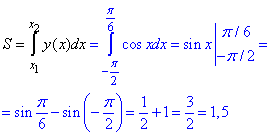
Тут не вказуємо, але пам'ятаємо, що площа вимірюється в одиницях квадратних.

ЗАВДАННЯ 4.1 Знайти площу плоскої фігури, що утворена лініями:
x=4-y², x+2y=4.
Розв'язання: Фігура обмежена x=4-y² - параболою з вершиною у точці O(4;0) і гілками вліво;
та x+2y=4 - прямою, що відтинається на осях у точках (4;0) і (0;2).
Знайдемо точки перетину графіків функцій із системи рівнянь:

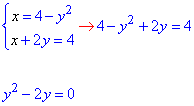
При її розв'язанні отримаємо дві точки

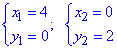
Графік параболи та прямої наведено на рисунку

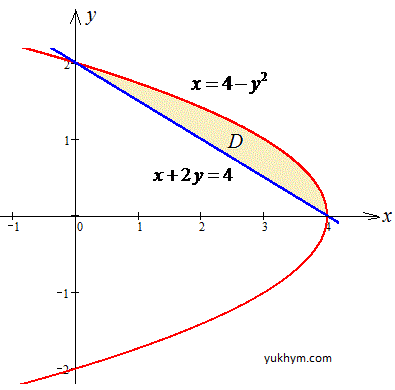
Запишемо межі інтегрування:
D: 0≤x≤4,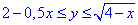
Тут маємо y=√(4-x) - рівняння верхньої частини параболи x=4-y2;
Обчислимо площу фігури знаходженням подвійного інтеграла:

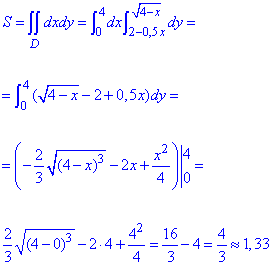
Площа рівна 1,33 одиниць квадратних.

ЗНО 2018. Завдання 31. Задано функції f(x)=x^3 і g(x)=4|x|.
1. Побудуйте графік функції f.
2. Побудуйте графік функції g.
3. Визначте абсциси точок перетину графіків функцій f і g.
4. Обчисліть площу фігури, обмеженої графіками функцій f і g.
Розв'язування: 1. Для побудови графіка функції f(x)=x³ знайдемо координати деяких точок і запишемо у таблицю: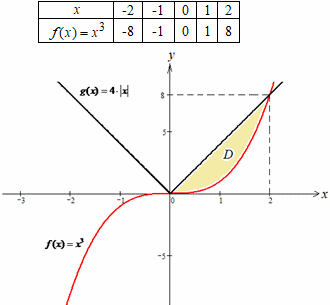
2. Графіком функції g(x)=4|x| є два промені зі спільним початком у точці (0;0) і є частиною прямих g(x)=±4x.
3. Знайдемо абсциси точок перетину графіків функцій f(x)=x³ і g(x)=4|x| для цього розв'яжемо x³=4|x| рівняння і знайдемо x

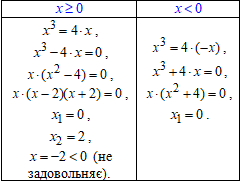
0, 2 - абсциси точок перетину графіків функцій.

4. Обчислимо площу фігури, обмеженої графіками функцій На проміжку x∈[0;2] маємо f(x)≤g(x), тому площа фігури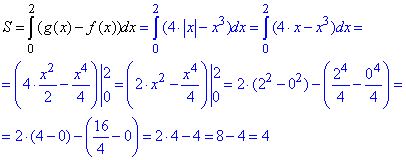
На цьому повну відповідь до тестового завдання завершено.

ЗАВДАННЯ 4.2 Знайти площу плоскої фігури, що утворена лініями:
y=2-x, y²=4x+4.
Розв'язання: y2=4x+4 - парабола з вершиною у точці O(-1;0) і гілками вправо;
y=2-x, x+y=2 - пряма, яка відтинається на осях у точках (2;0) і (0;2).
Складаємо систему рівнянь для знаходження точок перетину графіків заданих кривих:

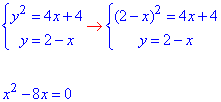
При розв'язанні отримаємо дві точки

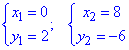
Графік області інтегрування має вигляд

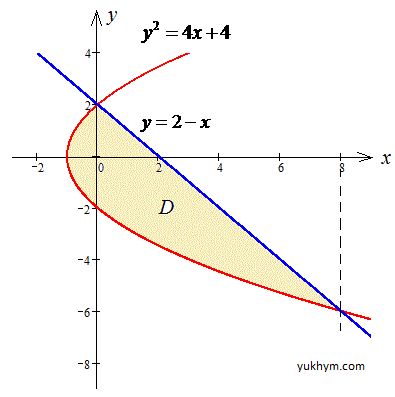
Межі в області D:
-6≤x≤2, 0,25y²-1≤y≤2-y.
Знаходимо площу фігури через криволінійний інтеграл:

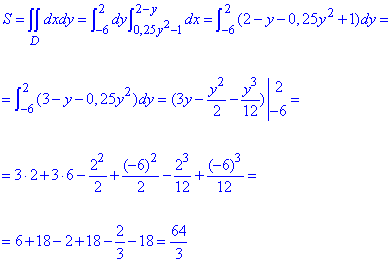
Кратний інтеграл не важко інтегрувати.

ЗАВДАННЯ 4.3 Знайти площу плоскої фігури, що утворена лініями:
x²+y²=4, x²+y²=4x.
Розв'язання: Область інтегрування обмежена x²+y²=4 - колом з центром у точці O₁(0;0) і радіусом R=2;
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² - коло з центром у точці O₁(2;0) і радіусом R=2.
Знайдемо точки перетину графіків заданих функцій з системи рівнянь:

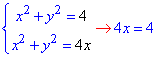
звідси

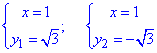
Графік фігури, площу якої шукаємо наведено далі

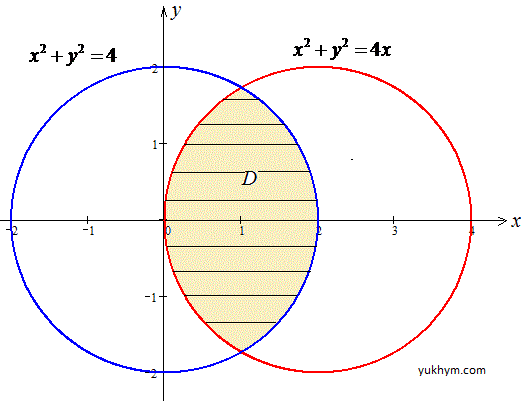
Розставимо межі в області D
(оскільки область симетрична відносно прямої y=0, то розглядатимемо її половину, а результат помножимо на 2):
D: 0≤y≤√3,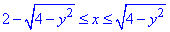
Тут записали:
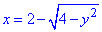- рівняння лівого півкола (x-2)²+y²=4;
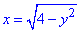- рівняння правого півкола x²+y²=4.
Обчислимо площу фігури через подвійний інтеграл:

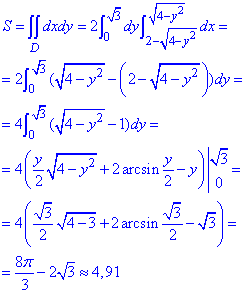
При інтегруванні отримали арксинуси, далі підставили межі та округлили кінцеве значення.

ЗАВДАННЯ 4.4 Знайти площу плоскої фігури, що утворена лініями:
x²+y²=2x, x²+y²=4x, y=x, y=0.
Розв'язання: Почнемо обчислення з аналізу того, що собою являє фігура, площу якої потрібно знайти.
x²+y²=2x, x²-2x+1 +y²=1, (x-1)²+y²=1² - коло з центром у точці O₁(1;0) і радіусом R=1.
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² - коло з центром у точці O₁(2;0) і радіусом R=2.
y=x - пряма, яка є бісектрисою першої та третьої чверті.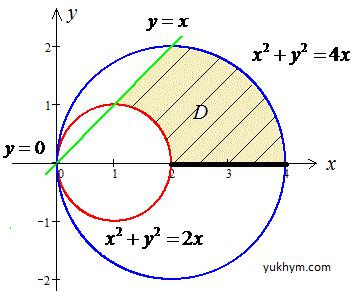
 
Оскільки поверхня обмежена колами, то доцільно перейти до полярних координат.

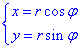
Знайдемо якобіан переходу:

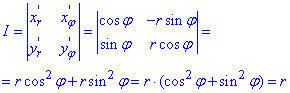
Запишемо задані функції в полярній системі координат:

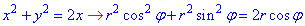
звідси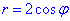

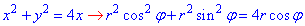
звідси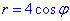
y=0, тоді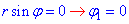
y=x, тоді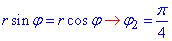
Це нам потрібно, щоб знати межі в новому інтегралі.
Межі інтегрування в полярній системі координат:

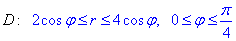
Знайдемо площу фігури, обмеженої заданими лініями:

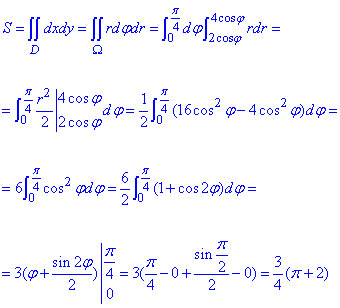
Кінцеве значення площі можна ще округлити.
З цього прикладу Ви ознайомилися як шукати площу в полярній системі координат.
В наступній статті розберемо ще кілька прикладів на знаходження площі фігур інтегруванням.