Знаменник геометричної прогресії із загальним членом bn=bn-1q=b1qn-1 знаходять за формулою частки наступного члена прогресії до заданого, або заданого до попереднього
q=bn/bn-1=bn+1/bn.
Це найпростіша формула, яка дозволяє обчислити знаменник прогресії в 9, 10 класах школи.
Далі приклади ускладнюють і на ЗНО тестах та олімпіадах доводиться вирішувати системи рівнянь та показникові рівняння для знаходження знаменника геометричної прогресії. Далі наведені приклади як зі шкільної програми, так і ЗНО та олімпіад в яких потрібно знайти знаменник прогресії.
Приклад 1 Визначити знаменник геометричної прогресії (bn), якщо b3=14, b4=98.
Обчислення: Є два способи розв'язання заданого прикладу.
Перший, простий в плані розрахунків на основі означення знаменника прогресії та формули вище.
А саме, що знаменник рівний частці наступного члена прогресії до заданого
q=b4/b3=98/14=7.
Другий спосіб, на основі формули n-го члена прогресії
b3=b1q3-1=b1q2=14
b4=b1q4-1=b1q3=98.
Поділимо друге рівняння на перше, в результаті отримаємо знаменник геометричної прогресії
b1q3/(b1q2)=q=98/14=7.
Відповідь: 7.
Приклад 2 Знайдіть знаменник геометричної прогресії, якщо b1=3, b3=147.
Обчислення: Для обчислення знаменника г/п застосуємо формулу загального члена геометричної прогресії
bn=bn-1q=b1qn-1.
Розпишемо її для 3-го номера
b3=b1q3-1=b1q2=147 .
Далі виразимо знаменник, розділивши 3-й член на 1-й
b3/b1=b1q2/b1=q2=147/3=49;
q2=49=7^2;
q=7.
На практиці подібним чином дістають просте показникове рівняння відносно q старших порядків, все залежить від того наскільки між собою рознесені задані члени геометричної прогресії.
Відповідь: 7.
Приклад 3 Як знайти знаменник геометричної прогресії якщо b1=1944, b4=576.
Обчислення: Схема обчислень аналогічна попередньому завданню:
Записуємо формулу загального члена г/п
bn=bn-1q=b1qn-1.
Для 4-го її члена отримаємо
b4=b1·q4-1=b1·q3
далі підставляємо b4, b1 та виражаємо q
576=1944·q^3;
q^3=576/1944;
q^3=8/27=(2/3)^3.
q=2/3.
Кубічне рівняння відносно q розв'язати тут не важко.
Відповідь: 2/3.
Пам'ятайте, що на практиці Вас, як правило, чекають подібні показникові рівняння q^n=a^n не старше 4-го порядку n=4.
ЗНО тести на знаходження знаменника г/п
Завдання 27. ЗНО 2018 Знаменник геометричної прогресії дорівнює 2/3, а сума чотирьох перших її членів дорівнює 65. Знайдіть перший член прогресії.
Розв'язування: У геометричній прогресії маємо q=2/3 - знаменник;
b1, b2, b3, b4 - відповідно перший, другий, третій і четвертий член геометричної прогресії.
За умовою маємо:
b1+b2+b3+b4=65,
враховуючи формулу bn=b1qn-1, отримаємо
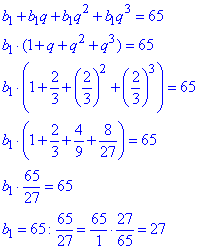
b1=27- перший член заданої геометричної прогресії.
Відповідь: 27.
Приклад 21.9 Визначити знаменник геометричної прогресії (bn), якщо b9=24, b6=-1/9.
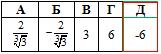
Обчислення: У г/п відомі b9=24, b6=-1/9 - члени г/п.
Використаємо формулу загального члена геометричної прогресії
bn=b1•qn-1.
Складаємо систему рівнянь з якої діленням виражаємо знаменник геометричної прогресії
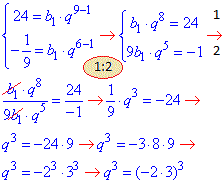
q=-2•3=-6 - шуканий знаменник.
Відповідь: -6 – Д.
Приклад 21.29 Установити відповідність між геометричними прогресіями (bn) (1–4), заданими двома членами, та їх знаменниками (А–Д).
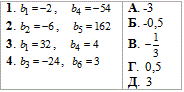Обчислення: З формули bn методом підстановки складаємо показникове рівняння або систему показникових рівнянь, звідки знаходимо знаменник q прогресії:
bn=b1qn-1.
1) b1=-2, b4=-54
b4=b1q4-1=-2q3=-54,
q3=27, q3=33,
звідси q=3.
1 - Д.
2) b2=-6, b5=162
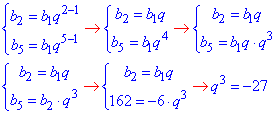
q^3=(-3)^3, звідси q=-3.
2 - А.
3) b1=32, b4=4
,
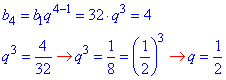звідси q=0,5.
3 - Г.
4) b3=-24, b6=3
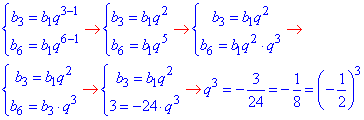
звідси q=-0,5.
4 - Б.
Приклад 4 Записати число 3,(14) у вигляді звичайного дробу.
Обчислення:Число 3,(14) = 3,1414… запишемо у вигляді наступної суми:
3,(14) = 3 + 0,14 + 0,0014 + 0,000014 + …
Доданки 0,14; 0,0014; 0,000014; … є членами нескінченно спадної геометричної прогресії з першим членом b1=0,14 і знаменником
q=0,0014/0,14=0,01.
Суму нескінченно спадної прогресії обчислимо за формулою
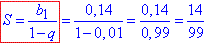
До суми слід додати 3, яка є на початку розкладу
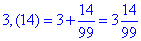
Таких завдань чимало, тому Ви повинні запам'ятати наведений алгоритм обчислень.
Приклад 5 Знайти знаменник геометричної прогресії у якій b5-b1=15; b4-b2=6.
Обчислення:За допомогою відомих членів та формули загального члена геометричної прогресії складемо систему рівнянь
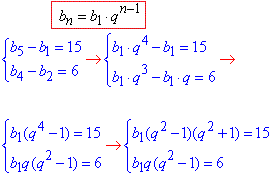
Розділимо перше рівняння системи на друге та, розписавши отриманий дріб, зведемо до квадратного рівняння
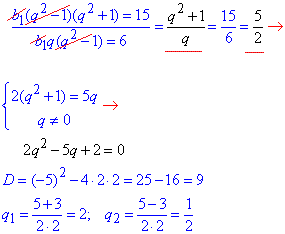Отримали два знаменники прогресії q=2, q=1/2, що задовольняють систему рівнянь.
Відповідь: 2, 1/2.
Цікавих завдань на знаходження знаменника прогресії можна привести ще чимало, але не всім з Вас вони допоможуть в навчанні. Хто цікавиться складними завданнями на прогресії може переходити до наступних уроків. Ми з Вами познайомимося з новими схемами розв'язання прикладів на арифметичну та геометричну прогресію.
