Щоб навчитися швидко розв'язувати комбінаторні задачі Вам потрібно до кожної із задач дати відповіді на три прості питання. Тоді Ви знатимете коли застосовувати комбінації, коли правильною є формула розміщень, а коли перестановки. Всі потрібні формули та схеми їх вибору наведені у таблиці:
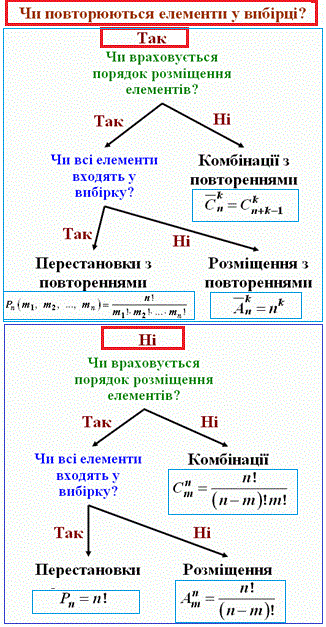
Все решта зводиться до правила суми, коли в умові потрібно знайти одну "або" іншу множину, та правило множення коли потрібно, щоб виконувалося "і" перше "і" друге і ... правило. Якщо наведені задачі Вам будуть важкі, то можете переглянути готові приклади комбінаторики з попередніх уроків, де більше розписані правила застосування кожної з наведених тут формул.
Комбінаторні задачі на формули перестановок, комбінацій та розміщень
Задача 1. Скількома способами можна пошити двокольоровий прапор зі смужками однакової ширини, якщо є матеріал восьми різних кольорів?
Розв'язання:Відповідь на завдання знаходять через розміщення з 8 по 2, оскільки один колір можна вибрати 8 способами, другий (8-1)=7 способами.
n=A82=8*7=56.
Задача 2. Скільки різних двоцифрових чисел можна скласти, використовуючи цифри 1, 2, 3, 4, 5, 6 якщо цифри:
1) повторюються;
2) не повторюються?
Розв'язання: Якщо цифри повторюються, то на перше місце можна поставити одну з 6, на друге також любу з 6, тому кількість двоцифрових чисел з повтореннями рівна
n=6*6=36.
2) Якщо цифри не повторюються, то на друге місце можна поставити всі цифри крім тої, що на першому місці, тому кількість рівна
n=6*5=30.
Але є задачі на цифри, які в такий спосіб не розв'язати.
Задача 3. Скільки трицифрових чисел можна скласти з цифр від 0 до 5, якщо:
1) цифри не повторюються;
2) отримане число має бути непарним;
3) число має бути кратним 5.
Розв'язання: Слід зауважити, що на перше місце не можна ставити 0, тому тут може бути одна з 5 цифр {1,2,3,4,5}. На другому місці 1 з 5 цифр, оскільки одну використали, зате добавився {0}, на третьому одна з 4.
Тому кількість різних трицифрових чисел рівна
N=5*5*4=100.
2) Якщо число непарне, то на третьому місці повинні стояти цифри 1,3,5
Тобто група має вигляд ХХ{1,3,5}, тоді на перші два місця потрібно вибрати одну з 5 цифр, включаючи 0. Тому на перше місце можна поставити 4 цифри без нуля і на друге одну з 4, включаючи 0.
Тому кількість таких цифр рівна
N1=4*4*3=48.
3) Число має бути кратним 5, тому вкінці повинно закінчуватися на 0 або на 5.
Якщо на 0, то на перші два місця потрібно ставити цифри {1,2,3,4,5}. Кількість способів це зробити рівна m1=5*4=20.
Якщо закінчується на 5, то на перше місце ставимо {1,2,3,4} без 0, на друге три з цієї групи+0, тому кількість різних чисел рівна m2=4*4=16.
Якщо маємо "або" то використовуємо комбінаторне додавання
N=m1+m2=36.
Завжди розмірковуйте, які можливі випадки, як можна розгалузити випадки. Для цього потрібно навчитися ставити правильні питання: Якщо ...?
Повірте розуміння прийде з практикою, тому більше розв'язуйте самостійно.
Задача 4. Дитині подарували набір з 10 цифр та 26 букв. Скількома способами можна скласти набір із:
1) двох букв або двох цифр;
2) двох букв і двох цифр.
Розв'язання: Дві букви з 26 можна вибрати розміщеннями з 26 по 2:
m1=A262=26!/24!=26*25=650.
Аналогічна схема вибору двох цифр з 10:
m2=A102=10!/8!=10*9=90.
1) "Або" в першій умові означає, що слід застосувати правило суми для обчислення кількості груп з 2 букв або 2 цифр:
N=m1+m2=650+90=740.
2) Кількість наборів з двох букв "і" двох цифр знаходимо за правилом добутку:
N1=m1*m2=650*90=58500.
Задача 5. На паралельних прямих а і в розміщено 10 і 7 точок відповідно. Скільки існує відрізків, що з'єднують точки прямих а і в?
Розв'язання: Нехай а1, а2, …, а10 – точки на прямій а,
в1, в2, …,в7— точки на прямій в.
Для кожної точки аі матимемо 7 відрізків, що сполучають цю точку з точками прямої в.
Кожному відрізку відповідатиме пара (аі ,вj).
За формулою комбінаторного множення кількість пар рівна
N=n·m.
Задача 6. Розклад одного дня містить 6 уроків. Визначити кількість таких розкладів при
виборі із 11 дисциплін.
Розв'язання: Для нас важливий порядок предмету в розкладі, томі якщо математика буде першим, а хімія - третім уроком, то це два різні розклади, і так для всіх 11 предметів. Тому тут не слід використовувати комбінації, тільки розміщення.
Тому кількість різних розкладів рівна:
A116=11!/(11-6)!=11*10*9*8*7*6=332640.
Задача 7. Скількома способами модна вибрати двох чергових із групи 17 чоловік?
Розв'язання: Тут неважливий порядок входження школярів в групу, а лише кількість різних груп, тому застосовуємо формулу комбінацій С з 17 по 2:
C172=17!/(17-2)!/2!=17*16/2=136.
Отже, можемо скласти 136 різних пар з двох чергових.
Задача 8.В ящику є 10 деталей. Скількома способами можна вибрати 3 деталі?
Розв'язання: Нам неважливий порядок вибору, головне щоб в наборі було три деталі. Кількість різних наборів знаходимо через комбінації з 10 по 3:
C103=10!/(10-3)!/3!=10*9*8/6=120.
Задача 9. Група з 7 осіб займає місця за круглим столом випадковим чином. Яка ймовірність того, що дві певні особи сядуть поруч?
Розв'язання: Кількість всіх можливих перестановок з 7 осіб рівна n=7!, кількість сприятливих розміщень
m=2*7*5!, тому ймовірність розсадити 7 осіб, щоб дві певні особи були поруч рівна частці:
P=m/n=2*7/(7*6)=1/3.
Задача 10. На пошті в продажу є 5 різних конвертів, 6 різних марок та 7 вітальних листівок. Скількома способами можна купити комплект, що містить конверт, марку та листівку?
Розв'язання:Відповідь отримаємо комбінаторним множенням:
n=5*6*7=210.
По другому ніяк, подумайте добре!
І таких задач безліч.
Для прикладу наступні:
1. В олімпійській збірній займаються танцями7 юнаків і 9 дівчат. Скількома способами можна вибрати одну пару для участі в олімпіаді?
2. У магазині є 5 різних ручок і 9 видів зошитів. Скількома способами можна скласти комплект з1 ручки й 1 зошита?
3. Скількома способами можна дібрати пару з однієї голосної і однієї приголосної букви у слові “ворона”?
Задача 11. Знайти кількість можливих слів, які можна утворити із букв слів "урок", "школа"(під словом будемо розуміти будь-який набір цих букв).
Розв'язання: Оскільки букви в слові "урок" не повторяються, а їх кількість рівна 4, то невідома кількість рівна перестановкам з 4 букв P4:
P4=4!=4*3*2=24
"Школа" містить 5 букв без повторень, тому кількість перестановок з 5 букв рівна P5
P5=5!=5*4*3*2=120
Задача 12. Знайти кількість можливих слів, які можна скласти із букв слів "ГІПОПОТАМ", "ВЕСЕЛКА", "АНАНАС".
Розв'язання: Оскільки букви в словах повторяються, то скористаємося формулою перестановок з повтореннями.
"ГІПОПОТАМ" містить 9 букв, з яких "П" та "О" зустрічаються двічі, тому кількість різних перестановок рівна:
P9(2,2,1,..,1)=9!/(2!*2!)=90720.
"ВЕСЕЛКА" містить 7 букв, дві з яких "Е", тому кількість різних перестановок рівна
P7(2,1,1,1,1,1)=7!/2!=2520.
Слово "АНАНАС" має з букви "А", всього 6 букв. Кількість різних наборів букв з 6 рівна:
P6(3,1,1,1)=6!/3!=120.
Задача 13. Скільки різних слів можна утворити переставляючи букви слів "МАТЕМАТИКА", "КОЛОСОК", "МІССІСІПІі".
Розв'язання: Слово "МАТЕМАТИКА" має 10 букв, три "А" та по дві "М", "Т".
Тому використовуємо формулу перестановок з повтореннями
P10(3,2,2,1,..)=10!/3!/(2!)^2=151200.
"КОЛОСОК" має 7 букв, три "О" та дві "К", тому кількість перестановок за аналогічним алгоритмом рівна
P7(3,2,1,11)=7!/(3!*2!)=420.
"Міссісіпі" має 9 букв, з яких "і" повторюється 4 рази, "с" - 3 рази.
Тому перестановками можна скласти
P9(4,3,1,1)=9!/(4!*3!)=2520.
Задача 14. Скільки різних "слів" можна утворити переставляючи букви слова "ВЕГЕТЕРІАНЕЦЬ", щоби букви "РІА" стояли поруч.
Розв'язання: Слово "МАТЕМАТИКА" має 10 букв, три "А" та по дві "М", "Т".
Тому використовуємо формулу перестановок з повтореннями
P10(3,2,2,1,..)=10!/3!/(2!)^2=151200.
"КОЛОСОК" має 7 букв, три "О" та дві "К", тому кількість перестановок за аналогічним алгоритмом рівна
P7(3,2,1,11)=7!/(3!*2!)=420.
Задача 15. Скількома способами можна переставити букви в слові «ОБОРОНОЗДАТНІСТЬ», щоб дві букви «о» не стояли поряд?
Розв'язання: Досить непростий приклад в плані розв'язку, тому уважно аналізуйте алгоритм отримання відповіді.
Слово містить 16 букв, з яких 4 "О", по дві "Н" та "Т".
План такий: знайти кількість різних перестановок слова без букви "О", тобто
"БРНЗДАТНІСТЬ", це 12 букв, дві "Н" та "Т"
Далі кількість способів розставити між ними по одній О, щоб їх було 4.
Перша кількість способів рівна перестановкам з повтореннями
m1=P12(2,2,1,..)=12!/(2!*2!)=119750400.
Далі букву "О" можна поставити між 12 буквами на (12-1)=11 місцях + перед ними + після них, тому є 11+1+1=13 варіантів для 4 "О", а кількість способів це зробити рівна комбінаціям
m2= C134=13!/9!/4!=715.
Відповіддю буде добуток знайдених значень:
N=m1*m2=85621536000.
Ось Вам можливий приклад одночасно на перестановки та комбінації.
Задача 16. Скільки способів розставити 10 різних книг на 2 полках порівну?
Розв'язання: Всім зрозуміло, що потрібно розставити по 5 книг на полку, яле виникає питання: Як, скількома способами?
Так як книжки різні, то порядок розміщення на полиці має значення, тому використовуємо формулу розміщень без повторень
m1=A105=10!/5!
Другу полку заповнюємо за формулою перестановок, оскільки всі 5 книг потрібно по різному розміщувати
m2=P5=5!
На двох полках означає і там, і там, тому значення перемножуємо:
n=m1*m2=10!
Задача 17. Скількома способами переноситься слово опеньки
Розв'язання: Будьте готові до будь-яких задач, логічних і не зовсім. Хтось схоче подробити дане слово і шукати факторіали, але відповідь проста:
"Опень-ки"
і других варіантів немає, бо це правило мови, що корінь не розриваємо ...
Тому деколи керуйтеся здоровим глуздом, а не всім, що Вас вчили.
Знайти ймовірність події
Задача 18. Монету підкидують три рази. Знайти ймовірності того що:
1) Герб випаде один раз;
2) Копійка не випаде ні разу;
3) Випаде і герб і копійка;
4) Герб випаде більше раз ніж копійка
Розв'язання: В задачах де мало варіантів, доцільно виписувати всі можливі події, щоб розуміти як обчислювати. При підкиданні монети тричі можливі наступні 6 варіантів:
{ГГГ; ГГК; ГКГ; КГГ; ГКК; КГК; ККГ; ККК}
Далі серед них вибираємо ті,які сприяють нашим умовам:
1) Є всього три випадки, що герб випаде один раз серед 6 усіх
{ГКК; КГК; ККГ}
тому ймовірність рівна
P=m/n=3/8.
2) Копійка не випаде ні разу означає тричі випаде герб {ГГГ}, тому ймовірність такої події
P1=m1/n=1/8.
3) Випишемо з нашої множини всі випадки коли випаде і герб і копійка:
{ГГК; ГКГ; КГГ; ГКК; КГК; ККГ}.
Це всі події окрім тричі випаде герб та тричі копійка, тому їх кількість рівна
P2=m2/n=6/8=3/4.
4) Герб випаде більше раз ніж копійка означає, що або два або три рази. Дехто не враховує останнього варіанту, бо тоді копійка не випадає жодного разу, тобто 0 раз, але 3>0, що відповідає умові.
Випишемо всі випадки:
{ГГГ; ГГК; ГКГ; КГГ}
та знайдемо імовірність події
P3=m3/n=4/8=1/2.
Задача 19. Імовірність того, що завтра піде дощ рівна 0,2, а ймовірність того, що піде сніг становить 0,4. Яка ймовірність, що завтра не буде опадів?
Розв'язання: Обчислимо від протилежної події.
Повна ймовірність рівна одиниці.
Щоб знайти ймовірність, що опадів не буде від повної ймовірності віднімемо ймовірності опадів
P=1-p1-p2=1-0,2-0,4=0,4
Розглянемо ще кілька задач, що мають відношення до грального бізнесу: підкидання костей та роздача карт в покері.
Задача 20.Гральний кубик підкидають тричі. Скільки різних послідовностей чисел можна при цьому отримати?
Розв'язання:На гранях маємо цифри від 1 до 6. Тому на першому місці може бути одна з 6 цифр. На другому одна з (6-1)=5 цифр, одна вже на першому місці і на останньому 1 з 4.
Кількість послідовностей рівна добутку можливих комбінацій цифр:
N=6*5*4=120.
Задача 21. Кидають гральний кубик два рази. Скільки може бути випадків, при яких цифра, що випаде при першому киданні, відрізняється від цифри, що випаде при другому киданні? Скільки випадків, що цифри однакові?
Розв'язання: При першому киданні може випасти від 1 до 6, тобто 6 різних значень. Щоб друга цифра була іншою є всього 5 граней, що відрізняються,
тому кількість таких випадків рівна:
N=6*5=30.
Задача 22. Гральний кубик кидають тричі. Знайти ймовірність, що шістка випаде один раз.
Розв'язання:Шістка може випасти першою, другою, або третьою. Решту разів випадуть грані, що не містять 6, їх 5.
Тому імовірність такої події рівна
p=3*1/6*5/6*5/6 =25/72≈0,347.
Задача 23. Яка ймовірність, що при киданні грального кубика двічі, обидва рази випаде парна кількість очок..
Розв'язання:До парних належать 2, 4, 6 три значення з 6.
Тому ймовірність, що випадуть парні значення рівна:
p=3/6*3/6=1/4=0,25.
Задача 24. Яка ймовірність, витягнути дві десятки з колоди, що має 24 карти
Розв'язання: Всі знають, що в колоді є по 4 карти кожної масті. Тому потрібно знайти кількість способів витягнути 2 десятки з 4 і розділити на кількість способів вибрати 2 карти з 24. Все це знаходимо через формулу комбінацій.
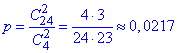
Задача 25. З колоди, що містить 36 карт (у колоді 4 тузи), виймають 5 карт. Знайти ймовірність, що серед цих карт буде хоча б один туз?
Розв'язання: Ми вже знаємо, що вибрати 5 карт з 36 можна С з 36 по 5 способами.
Далі подія - вибрати хоча б один туз означає, що або 1 або 2 або 3 або 4. Це 4 формули комбінацій, щоб їх не знаходити краще від повної ймовірності віднімемо ймовірність, що серед цих карт не буде жодного туза.
А кількість способів це зробити рівна С з (36-4 тузи)=32 по 5.
Обчислюємо ймовірність
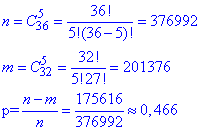
Задача 26. Яка ймовірність роздати 4 тузи з 6 карти, коли в колоді 36?
Розв'язання: Чотири тузи з 4 можна вибрати єдиним способом, залишається вибрати 3 карти з (36-4)=32. Тому кількість сприятливих способів рівна добутку комбінацій
m=C44*C322=1*32*31/2=496.
Всеможлива кількість способів вибрати 6 карт з колоди рівна комбінації з 36 по 6:
n=C366=36!/(6!*30!)=1 947 792.
Вже можна побачити, що ймовірність такої події прямує до нуля
p=m/n=496/1 947 792≈0,00025.
Задача 27. Для того щоб виграти в лотерею потрібно вгадати 4 з 35 цифр. Знайти ймовірність вгадати цифри, якщо вони не повторюються?
Розв'язання: Тут не важливий порядок, а лише правильний набір цифр. Тому нам потрібно знайти кількість способів вибрати 4 різні цифри з 35, а це як Ви здогадались дорівнює С з 35 по 4:
n=C354=35!/(4!*31!)=35*34*33*32/24=52360.
Це і є кількістю різних комбінацій скласти виграшний білет, а він лише один, тому імовірність виграшу:
p=1/52360=0,000019.
Ось чому Вам майже нереально виграти в лотерею, а тим хто організував гральний бізнес завжди залишаються у виграші.
Вчіть ймовірність, щоб знати свої шанси на успіх. Для цього подружіться з факторіалами, адже Вам доведеться їх спрощувати протягом усього курсу теорії ймовірностей.


