Далі наведені готові відповіді до ЗНО тестів на тему 41. Координати. На попередньому уроці розглянули приклади на точки та вектори, сьогодні продовжимо обчислювати координати точок, довжини між точками, площі трикутників, квадратів, . З наведеними прикладами Ви повинні швидко розібратися, адже далі підуть уроки на зведення рівнянь кіл та сфер до канонічного вигляду та складніші завдання пов'язані з координатами.
Приклад 41.16 Дано ABCD – паралелограм з трьома вершинами A(-4;1;5), B(-5;4;2), C(3;-2;-1). Знайти координати вершини D.
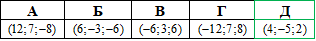
Розв'язування: Для відшукання четвертої вершини скористаємося властивістю про те, що у паралелограма ABCD діагоналі AC і BD в точці перетину (S) діляться навпіл:
AS=SC, BS=SD. Схематичний рисунок паралелограма має вигляд
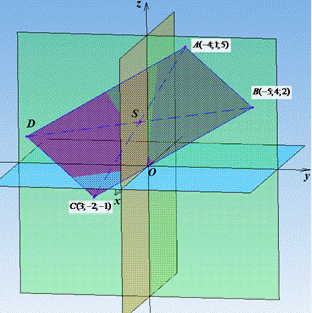
Спочатку знайдемо координати центра S - середини відрізка (діагоналі) AC за відомими координатами:
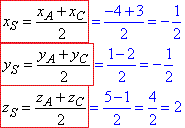
Отримали 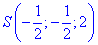 - координати точки перетину діагоналей AC і BD.
- координати точки перетину діагоналей AC і BD.
Із умови, що BS=SD складаємо рівняння для знаходження координати точки D і розв'язуємо:
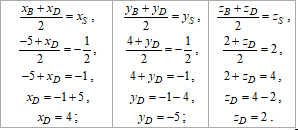
D(4;-5;2) - шукана вершина.
Відповідь: (4;-5;2) – Д.
Приклад 41.17 Дано ABCDA1B1C1D1 – куб. A(7;0;0), B(5;0;0),C1(5;2;2). Знайти координати вершини D1.
Розв'язування:Обчислення проведемо по аналогічній схемі з попереднім завданням: за відомими вершинами визначимо центр куба як середину між точками, а далі складемо рівняння за відомою вершиною центром для обчислення D1.
У куба ABCDA1B1C1D1 діагоналі AC1 і BD1 (всі його діагоналі) в точці перетину (S) діляться навпіл:
AS=SC1, BS=SD1.
Рисунок до задачі має вигляд
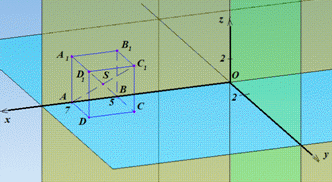
Спочатку знайдемо координати точки S - середини відрізка (діагоналі) AC1:
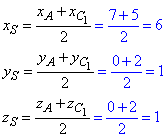
Звідси, S(6;1;1) - координати точки перетину діагоналей AC1 і BD1.
Із умови, що BS=SD1 складемо 3 рівняння для знаходження координати вершини D1:
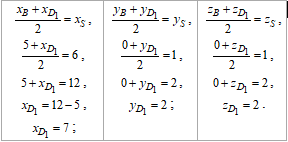
Шукана вершина куба має координати D1(7;2;2).
Додатково, із умови координат точок A(7;0;0), B(5;0;0), C1(5;2;2) - деяких вершин куба ABCDA1B1C1D1 помічаємо, що його сторони паралельні осям координат, тому інші вершини куба матимуть координати:
A1(7;0;2), B1(5;0;2), C(5;2;0), D(7;2;0).
Вчіть зауважувати подібні аналогії з побудови та координатного запису, часто це спрощує хід розрахунків.
Відповідь: (7;2;2) – Г.
Приклад 41.18 Дано трикутник ABC з вершинами A(2;2;-4), B(2;-1;-1), C(3;-1;-2). Знайти зовнішній кут при вершині B.
А | Б | В | Г | Д |
60 | 90 | 120 | 135 | інша відповідь |
Розв'язування: Схема обчислень полягає у знаходженні косинуса кута через скалярний добуток двох векторів, що виходять з однієї вершини трикутника.
Для цього зі сторін трикутника ABC сформуємо вектори:
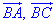 зі спільним початком при вершині B.
зі спільним початком при вершині B.
Рисунок трикутника в просторі має вигляд
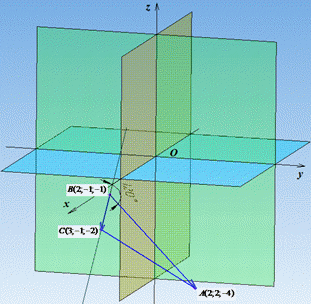
Знайдемо координати ВА, ВС:
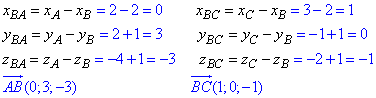
Обчислимо скалярний добуток векторів за формулою
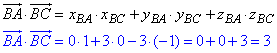
Знайдемо модулі (довжини) векторів BA і BC:
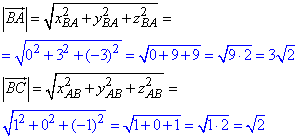
Маючи довжини між точками, знайдемо косинус кута між векторами BA і BC - внутрішній кут B трикутника ABC за формулою:
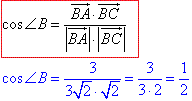
Косинус рівний 0,5, отже робимо висновок що кут рівний ∠B=60.
Знайдемо зовнішній кут при вершині B (за означенням зовнішнього кута трикутника):
180-∠B=180-60=120.
(В цьому завданні було використано метод векторів у просторі, який детально розглядатиметься у розділі 42).
Відповідь: 120 – В.
Приклад 41.19 Точки A(2;4) і C(5;8) є вершинами квадрата ABCD. Знайти площу цього квадрата.
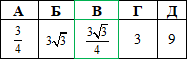
А | Б | В | Г | Д |
2,5 | 5 | 12,5 | 25 | 20 |
Розв'язування: У квадрата ABCD відрізок AC називається діагоналлю. Виконаємо допоміжний рисунок до завдання
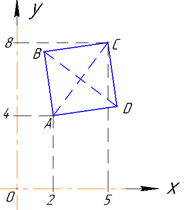
Площу квадрата ABCD можна обчислити за формулою:
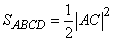
Її без проблем можете знайти онлайн або вивести через сторони квадрата.
Обчислимо квадрат довжини відрізка (діагоналі) AC:
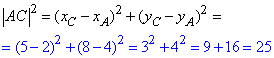
Знайдемо площу квадрата ABCD:
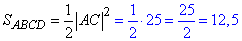
Відповідь: 12,5 – В.
Приклад 41.20 Точки A(-1;0;2) і B(0;1;1) є вершинами правильного трикутника. Знайти площу цього трикутника.
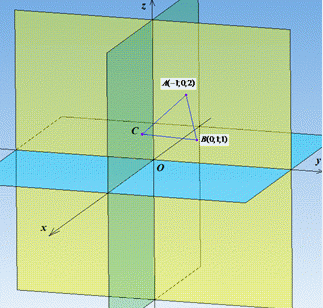
Розв'язування: У правильного (рівностороннього) ΔABC всі сторони рівні:
|AB|=|AC|=|BC|.
Тому, площу трикутника ABC можна обчислити за формулою:
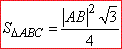
Визначимо квадрат довжини відрізка (сторони) AB із залежності:
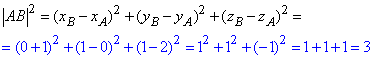
Знайдемо площу правильного трикутника ABC:
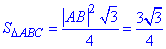
Серед варіантів тестів вірний результат містить пункт В.
Відповідь: 3√3/4 – В.
Приклад 41.22 При паралельному перенесенні точка A(1;3;2) переходить у точку A'(3;0;1). Установити відповідність між точками (1–4) та точками (А–Д), утвореними при цьому паралельному перенесенні.

Розв'язування: Обчислимо координати вектора 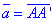 , при якому здійснюється паралельне перенесення з точки A(1;3;2) в точку A'(3;0;1):
, при якому здійснюється паралельне перенесення з точки A(1;3;2) в точку A'(3;0;1):
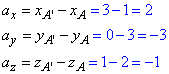
Остаточно, a(2;-3;-1).
Знайдемо координати точок M’(x;y;z), у яку переходять точки Mn при паралельному перенесенні на вектор a(2;-3;-1):

Обчислення під силу школярам і полягають в додаванні до координат заданих вершин координат вектора AA'.
(Завдання повністю аналогічне до завдання Приклад 41.7, тому рисунки не наводимо).
Приклад 41.24 Установити відповідність між парами точок (1–4), та відстанями між цими точками (А–Д).

Розв'язування: Відстань між точками M і N (довжина відрізка MN) в просторі знаходимо за формулою:

Послідовно для кожного пункту тестів підставляємо координати та виконуємо обчислення:
1) M1(1;3;4), N1(2;1;2)
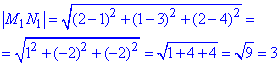 А;
А;
2) M2(3;5;1), N2(0;1;1)
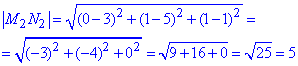 В;
В;
3) M3(-2;3;4), N3(6;3;-2)
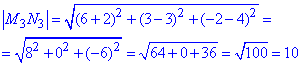 Д;
Д;
4) M4(1;-2;5), N4(1;10;0)
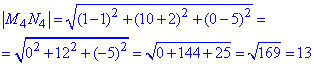 Б.
Б.
В тестах добре, що підказкою є варіанти відповідей. Тому, якщо отримали якесь друге значення, то скоріш за все допустили помилки в обчисленнях.
Вивчайте та запам'ятовуйте формули, без яких Ви не зможете вирішити задач в координатах.


