Продовжуємо аналіз готових відповідей із ЗНО тестів на тему 41. Координати. Сьогодні розберемо завдання де потрібно скласти рівняння прямої , та знайти відстань між точками. Це не прості приклади на застосування готових формул, тут потрібно виконувати побудову та добре знати геометрію.
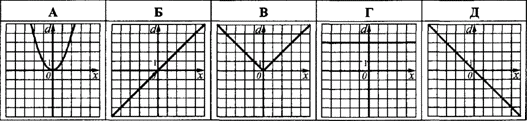
Приклад 41.21 d(x) – відстань від точки M(x;0;0) до площини yOz. Який з наведених графіків є графіком функції d=d(x)?
Розв'язування: Точка M(x;0;0) належить осі Ox і приймає будь-яке її значення, ордината y та апліката z при цьому дорівнюють 0.
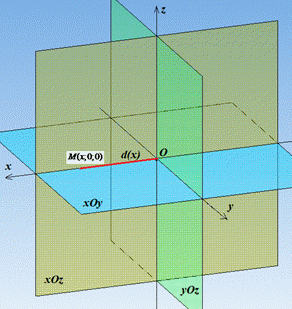
Звідси слідує, що відстань від точки M(x;0;0) до площини yOz дорівнює модулю абсциси цієї точки, тобто
d(x)=|x|.
Серед запропонованих в тестах відповідей слід обрати ту, яка містить графік модуль функції. Такий варіант зображений на рисунку В.
Відповідь: В.
Приклад 41.25 На осі ординат знайти ординату точки, рівновіддаленої від точки A(-4;2) і початку координат.
Розв'язування: Побудуємо схематичний рисунок до задачі
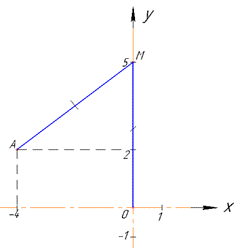
Нехай M(0;y) - точка на осі ординат (Oy), ординату y якої потрібно знайти.
Оскільки точка M(0;y) рівновіддалена від точки A(-4;2) і точки O(0;0) (початку координат), то |AM|=|OM| (довжини відрізків AM та OM рівні), відповідно рівні квдрати модулів
|AM|2=|OM|2.
Обчислюємо довжини векторів
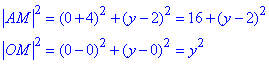
Прирівняємо дві останні рівності та з отриманого рівнянння виразимо невідому y:
16+(y-2)^2=y^2,
16+y^2-4y+4=y^2,
-4y=-20,
y=20:4=5.
Запам'ятайте схему обчислень до завдання.
Точка M з координатами (0;5) рівновіддалена від точки A(-4;2) і початку координат.
Відповідь: 5.
Приклад 41.26 Скласти рівняння прямої, яка проходить через точку M(-2;5) й утворює з додатним напрямом осі абсцис кут 45 градусів. У відповідь записати абсцису точки перетину прямої з віссю абсцис.
Розв'язування: Рівняння прямої на площині має вид: y=k•x+b,
де k - кутовий коефіцієнт нахилу прямої до осі абсцис (Ox);
k=tg(φ),
φ - кут нахилу прямої з додатнім напрямом осі абсцис, за умовою φ=45;
b - ордината перетину прямої з віссю ординат (Oy).
Обчислюємо кутовий коефіцієнт k=tg(45)=1.
Наведемо рисунок прямої під кутом 45 градусів до осі абсцис.
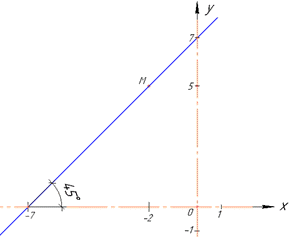
Щоб знайти параметр b підставимо координати точки M(-2;5) (тут x=-2 і y=5) і значення k=1 у загальне рівняння прямої:
5=1•(-2)+b,
5=-2+b,
b=5+2=7.
Отримали таке рівняння прямої y=x+7.
При y=0 знаходимо
x=-7 - абсцису точки перетину прямої з віссю абсцис (Ox).
Відповідь: -7.
Приклад 41.27 Знайти:
1) площу трикутника;
2) периметр трикутника, обмеженого осями координат і прямою 4x+3y=24.
Розв'язування: Знайдемо координати трикутника AOB, сторонами якого є осі координат і пряма 4x+3y=24.
Наперед наведемо рисунок трикутника, який досліджуємо
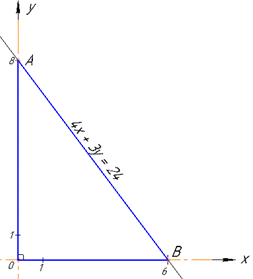
Вершина O(0;0) - початок координат, кут при цій вершині дорівнює 90 тому ΔAOB - прямокутний з катетами AO і OB, гіпотенузою AB.
Вершина A(0;y) належить осі ординат (Oy).
З умови перетину прямої 4x+3y=24 з віссю ординат (x=0) знайдемо ординату точки A:
4•0+3y=24,
3y=24,
y=24:3=8
Отже, A(0;8) - координати вершини A, звідси слідує, що катет AO=8. Такі пояснення потрібні, оскільки нам не тільки потрібно знайти координати вершин трикутника, а й визначити відстані між вершинами, після чого обчислити периметр та площу трикутника.
Вершина B(x;0) належить осі абсцис (Ox).
З умови перетину прямої 4x+3y=24 з віссю абсцис (y=0) знайдемо абсцису точки B:
4x+3•0=24,
4x=24,
x=24:4=6.
Отже, B(6;0) - координати вершини B, звідси слідує, що катет OB=6.
Гіпотенузу (довжину вдрізка) AB знайдемо як відстань між точками A(0;8) і B(6;0):
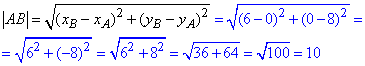
(як бачимо на виході все одно отримали запис звичайної теореми Піфагора).
Отже, AB=10 - довжина гіпотенузи прямокутного ΔAOB.
Знаходимо площу прямокутного трикутника ΔAOB через півдобуток основи на висоту:
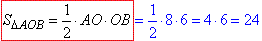
Обчислимо периметр трикутника ΔAOB:
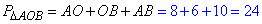
Відповідь: 24; 24.
Приклад 41.28 Знайти квадрат довжини медіани AA1 трикутника ABC, якщо A(3;-2;1), B(3;1;5) і C(4;0;3).
Розв'язування: Медіана AA1 трикутника ABC ділить сторону BC навпіл, тобто BA1=A1C.
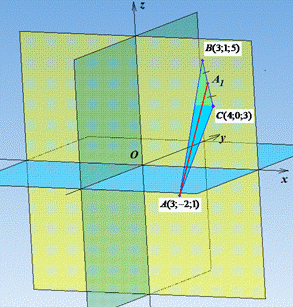
Для знаходження координати точки A1 - середини відрізка (сторони) BC застосуємо формулу:
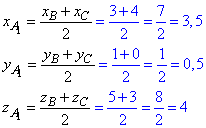
Остаточно A1(3,5;0,5;4).
Знайдемо квадрат довжини медіани AA1 як квадрат відстані між точками A(3;-2;1) і A1(3,5;0,5;4):
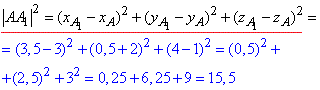
Ось такі розрахунки Ви маєте вміти виконувати, щоб легко скласти вступні іспити у ВУЗи.
Відповідь: 15,5.
Приклад 41.31 Точка M(2;6;3) - середина відрізка, кінці якого лежать на осі Ox і на площині yOz. Знайти довжину відрізка.
Розв'язування: Завдання досить складне для школярів, що погано уявляють собі прямі та ін. в просторі. В умові достатньо підказок, щоб вирішити завдання, і в цьому зараз переконаєтеся (див. рисунок).
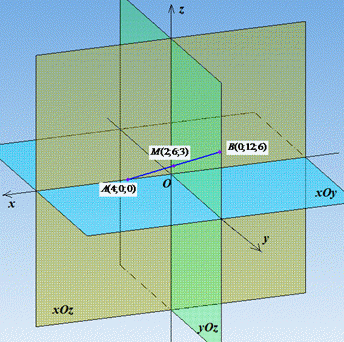
Нехай точка A один кінець відрізка, який лежить на осі абсцис (Ox), тоді її координати A(xA;0;0) (на осі Ox ордината y і апліката z дорівнюють нулю).
Нехай точка B інший кінець відрізка, який лежить на площині yOz, тоді її координати B(0;yB;zB) (на площині yOz абсциса x дорівнює нулю).
Отримали відрізок AB, серединою якого є точка M(2;6;3).
Знайдемо координати кінців A(xA;0;0) і B(0;yB;zB) відрізка AB з формули про середню точку:
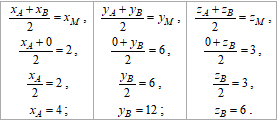
Знайшли A(4;0;0) і B(0;12;6) - координати кінців відрізка AB.
Обчислимо довжину відрізка AB як відстань між точками A(4;0;0) і B(0;12;6):
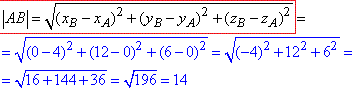
Запам'ятайте цю формулу, нею часто доводиться користуватися в задачах на координати.
Відповідь: 14.
Приклад 41.32 На ділянці, яка обмежена з двох боків взаємно перпендикулярними дорогами, посадили сад. Відстань від яблуні до першої дороги становить 3м, а до другої – 4м. Відстань від груші до першої дороги дорівнює 6м, а до другої – 8 м.
Знайти відстань між цими деревами.
Розв'язування: Зробимо математичну модель задачі. Ділянку разом з дорогами замінимо на систему координат, осями якої будуть дороги. Початок координат буде точка перетину доріг (дороги за умовою перпендикулярні). Дерева, що ростуть у саду замінимо на точки, зокрема, яблуню позначимо як точку A, а грушу – як точку B.
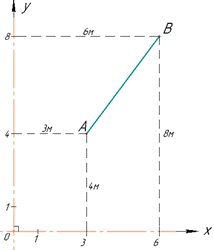
Першу дорогу позначимо за вісь ординат (Oy), а другу дорогу – за вісь абсцис (Ox). Відповідні відстані від дерев до доріг і будуть координатами точок A(3;4) і B(6;8) (дивись рисунок).
Знайдемо відстань між точками A(3;4) і B(6;8) – довжину відрізка AB:
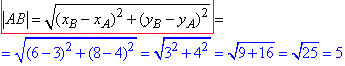
Шукана відстань між деревами 5м.
Ще раз перегляньте пояснення до цієї задачі та попередніх та зацініть, наскільки добре мати просторову уяву і вміння розбивати складні завдання на прості дії.
Відповідь: 5.
Якщо маєте цікаві завдання, які розкривають не описані тут алгоритми розв'язування прикладів на координати, то діліться з нами. Ми їх красиво оформимо та опублікуємо!


