Модуль вектора. Обчислення довжини вектора

Для знаходження довжини вектора AB з початком у точці A(a_x;a_y) та кінцем в точці B(b_x;b_y) потрібно від кінця вектора відняти початок
AB(b_x-a_x;b_y-a_y).
Модуль (довжина) вектора рівний кореню квадратному з суми квадратів проекцій вектора на осі

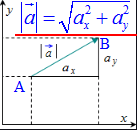
В просторі добавиться третя координати, формули аналогічні наведеним і далі їх будемо використовувати для розв'язування ЗНО тестів. В поясненнях до завдань ми не ставили знак вектора, хоча Вам це робити при розв'язуванні потрібно. За правильний приймайте запис векторів, який фігурує у формулах.

Приклад 42.14 Знайти координати вектора a, зображеного на рисунку.

Розв'язування: Початково рисунок має тільки сітку, тому дописуємо значення по осях.

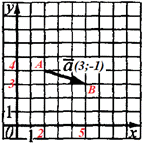
Випишемо координати початку A і кінця B вектора a:
A(2;4), B(5;3).
Запишемо координати вектора a як різницю координат кінця B(5;3) та початку A(2;4):
a(5-2;3-4)=(3;-1).
Відповідь: (3;-1). – Г.

Приклад 42.5 Дано точки A(5;-6;7) і B(8;-2;7). Знайти абсолютну величину вектора AB.

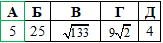
Розв'язування: Знайдемо координати вектора AB(x;y;z):
(потрібно від координат кінця B(8;-2;7) вектора AB відняти координати початку A(5;-6;7)).
AB(8-5;-2+6;7-7)=(3;4;0).
Знайдемо абсолютну величину (модуль, довжину) вектора |AB|:

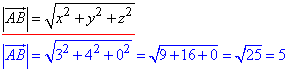
Відповідь: 5 – А.

Приклад 42.6 Знайти довжину вектора AB, якщо A(-1;1;-1) і B(-1;1;1).

Розв'язування: Знайдемо координати вектора AB(x;y;z):
(від кінця B(-1;1;1) вектора AB віднімаємо координати початку A(-1;1;-1)).
AB(-1+1;1-1;1+1)=(0;0;2).
Знайдемо довжину (абсолютну величину) вектора |AB|:

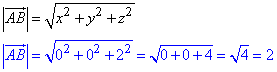
Відповідь: 2 – Б.

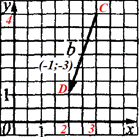
Приклад 42.15 Знайти абсолютну величину вектора b, зображеного на рисунку.

Розв'язування: Випишемо за побудовою координати початку C і кінця D вектора b:
C(3;4), D(2;1).
Координати вектора b обчислимо як різницю координат кінця D(2;1) та початку C(3;4):
b(2-3;1-4)=(-1;-3).
Знайдемо абсолютну величину (довжину) вектора b(-1;-3):

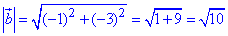
Відповідь: √10 – В.

Приклад 42.22 Знайти модуль вектора 2a+3b, якщо a(1;2), b(1;0).

 Розв'язування: Перш за все побудуємо задані вектори в декартовій площині.

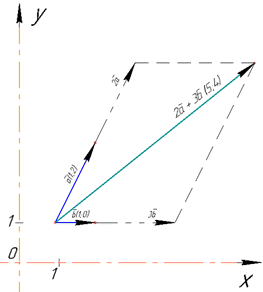
Помножити вектор на число означає помножити кожну координату на це число:
2a=(2•1;2•2)=(2;4),
3b=(3•1;3•0)=(3;0).
Додати вектори означає додати їх відповідні координати:
2a+3b=(2+3;4+0)=(5;4).
Обчислимо модуль (довжину) вектора 2a+3b:

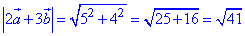
Відповідь: √41 – А.

Приклад 42.39 Дано вектор a(2;1;-3). Знайти квадрат довжини вектора b, якщо a•b=7 і вектор b колінеарний вектору a.
Розв'язування: Оскільки вектор b колінеарний вектору a(2;1;-3), то їх відповідні координати пропорційні. Нехай x – коефіцієнт пропорційності, тоді b(2x;x;-3x).
Знайдемо x з умови, що a•b=7 (скалярний добуток векторів a і b дорівнює 7):

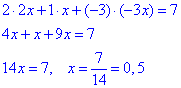
Отже, отримали b(1;0,5;-1,5).
Знайдемо квадрат довжини вектора b(1;0,5;-1,5):
.
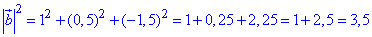Відповідь: 3,5.

Далі підуть складніші завдання на довжину суми та різниці векторів, які вимагають знання наступних формул скалярного добутку.

Приклад 42.18 Вектори a і b утворюють кут 135⁰,|a|=2, |b|=2√2. Знайти |a-b|.

Розв'язування: Виконаємо схематичний рисунок векторів

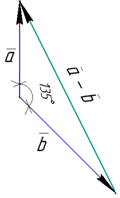
Модуль (довжина) різниці векторів |a-b| шукається за допомогою скалярного добутку векторів наступним чином:

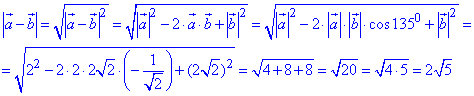
Нагадаємо правило обчислення косинуса для кутів більших від 90⁰:

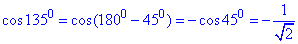
Відповідь: 2√5 – Б.

Приклад 42.19 Дві сили F1 і F2 утворюють між собою кут 120⁰. |F1|=|F2|=10H. Знайти модуль рівнодійної цих сил.

Розв'язування: Оскільки у математиці сили позначаються векторами, то рівнодійна двох сил F1 і F2 є векторною сумою F:


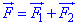
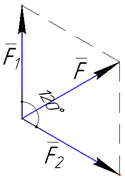
а модуль рівнодійної |F| дорівнює довжині (модулю) вектора F. Отже,
Мовою формул цьому відповідає запис

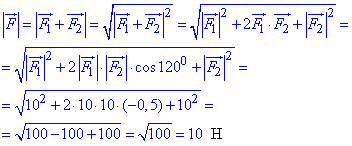
тут cos(120⁰) знаходимо, виходячи з періодичності косинуса

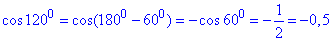
На рисунку додавання векторів (F=F1+F2) виконано за правилом паралелограма.
Відповідь: 10 Н – Б.

Приклад 42.34 Знайти довжину вектора a-b-c, якщо |a|=2, |b|=3, |c|=4, ∠(a;b)=60, ∠(b;c)=90, ∠(a;c)=120 й обчислити його значення з точністю до 0,01.
Розв'язування: Знайдемо скалярний добуток векторів a і b:

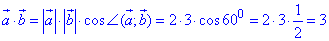
отже отримали a•b=3.
Знайдемо скалярний добуток векторів b і c:
Оскільки ∠(b;c)=90, тобто b⊥c, то b•c=0.
Знайдемо скалярний добуток векторів a і c:
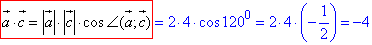, отже отримали a•c=-4.
Знайдемо довжину (модуль) вектора a-b-c, який містить в собі скалярні добутки і довжини заданих векторів a, b, c:

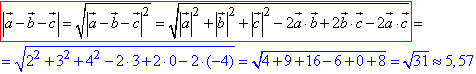
Відповідь: 5,57.

Попереду ще кілька публікацій на вектори з яких Ви дізнаєтеся схеми розв'язування прикладів на перпендикулярність та паралельність векторів, знаходження кута між векторами.
Умови перпендикулярності та колінеарності досить важливі на практиці, тому обов'язково пробіжіться по готових прикладах!

Вас може зацікавити:
1. Знаходження координат точок, довжин між точками
2. Довжина вектора. Кут між векторами
3. Знаходження координат точок, довжин між точками
4. Розклад вектора за базисом